JUMP TO TOPIC
 The extreme value theorem states that a function has both a maximum and a minimum value in a closed interval $[a,b]$ if it is continuous in $[a,b]$.
The extreme value theorem states that a function has both a maximum and a minimum value in a closed interval $[a,b]$ if it is continuous in $[a,b]$.
We are interested in finding the maxima and the minima of a function in many applications. For example, a function describes the oscillation behavior of an object; it will be natural for us to be interested in the highest and lowest point of the oscillating wave.
In this topic, we will discuss in detail about extreme value theorem, its proof, and how to calculate the minima and maxima of a continuous function.
What Is Extreme Value Theorem?
The extreme value theorem is a theorem that determines the maxima and the minima of a continuous function defined in a closed interval. We would find these extreme values either on the endpoints of the closed interval or on the critical points.
On critical points, the derivative of the function is zero. For any continuous closed interval function, the first step is to find all the critical points of a function and then determine the values on these critical points.
Also, evaluate the function on the endpoints of the interval. The highest value of the function would be the maxima, and the lowest value of the function would be the minima.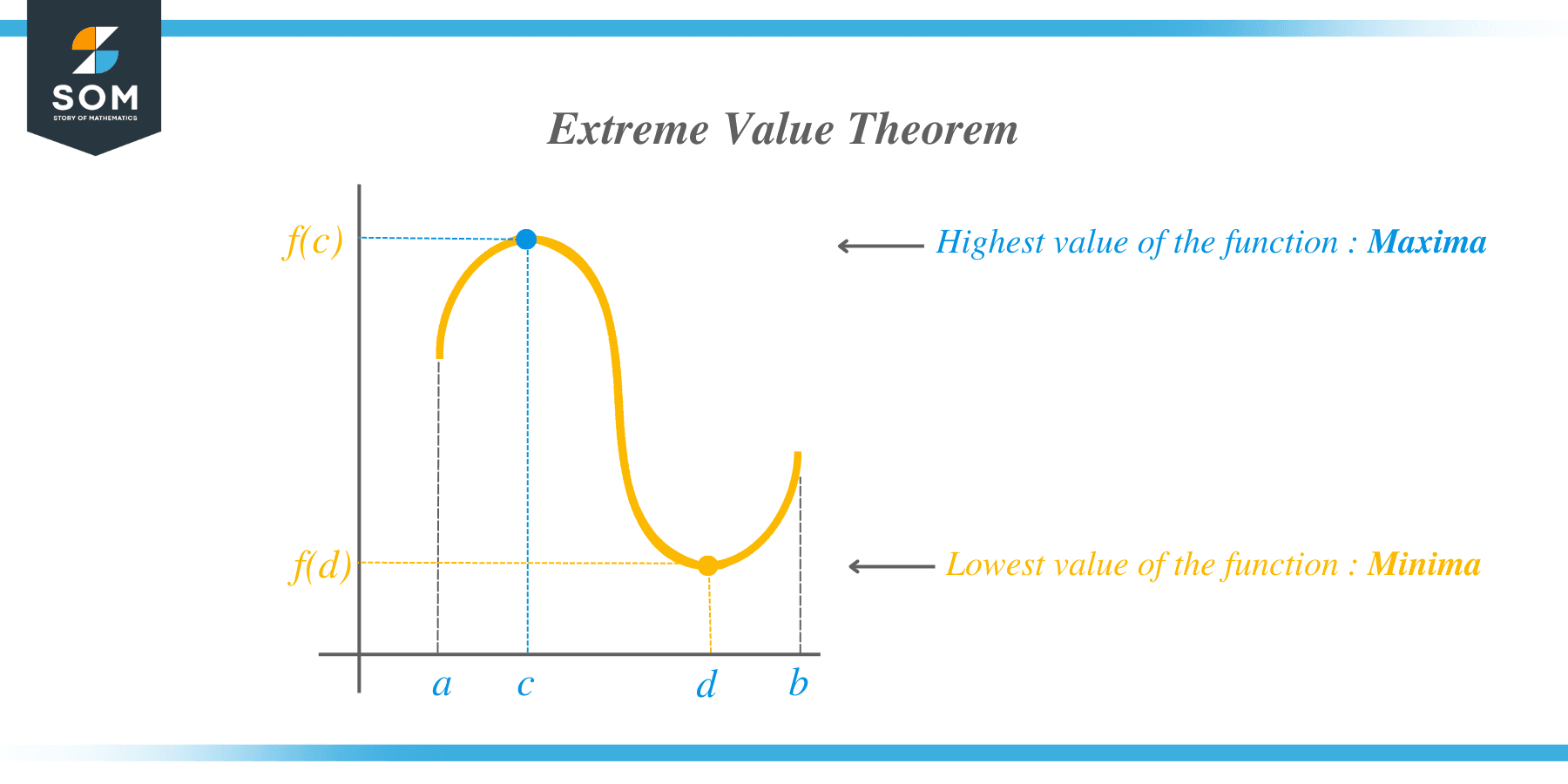
How To Use Extreme Value Theorem
The procedure of using the extreme value theorem is given in the following steps:
- Make sure the function is continuous on a closed interval.
- Find all the critical points of the function.
- Calculate the value of the function at those critical points.
- Calculate the value of the function on the endpoints of the interval.
- The highest value among all the calculated values is the maxima, and the least value is the minima.
Note: If you have confusion regarding a continuous function and a closed interval, see the definitions at the end of this article.
Proof of Extreme Value Theorem
If $f(x)$ is a continuous function in $[a,b]$, then it must have a least upper bound in $[a,b]$ (by the Boundedness theorem). Let $M$ is the least upper bound. We have to show that for a certain point $x_o$ in the closed interval $[a,b]$, $f(x_o)=M$.
We will prove this by using the contradictory method.
Suppose there is no such $x_o$ in $[a,b]$ where $f$ has a maximum value $M$.
Consider a function:
$g(x) = \dfrac{1}{M\hspace{1mm} – \hspace{1mm}f(x)}$
As we have assumed there is no M for the function f(x), hence g(x) > 0 for all values of x and as M – f(x) is continuous, so the function $g(x)$ will also be a continuous function.
So function g is bounded in the closed interval $[a,b]$ (again by Boundedness theorem), and hence there must be a $C > 0$ such that $g(x) \leq C$ for every value of $x$ in $[a,b]$.
$g(x) \leq C$
$\dfrac{1}{M\hspace{1mm} – \hspace{1mm}f(x)} \leq C$
$M – f(x) \leq \dfrac{1}{C}$
$M – \dfrac{1}{c}\geq f(x)$ (1)
So according to equation (1), $M – \dfrac{1}{C}$ is the upper bound of function $f(x)$, but it is smaller than $M$, so it contradicts the definition of M being the least upper bound of $f$. As we have derived a contradiction, our original assumption must be false and hence it is proved there is a point $x_o$ in the closed interval $[a,b]$ where $f(x_o) = M$.
We can obtain the proof for minima by applying the above arguments on $-f$.
Example 1:
Find the extreme values for the function $f(x) = x^{2} – 6x + 10$ on the closed interval $[0,4]$.
Solution:
This is a quadratic function; the given function is continuous and is bounded by the closed interval $[0,4]$. The first step is to find the critical values of the given function. To find the critical values, we have to differentiate the function and put it equal to zero.
$f(x) = x^{2} – 6x + 10$
$f'(x) = 2x – 6$
Now by putting $f'(x) = 0$, we get
$2x – 6 = 0$
$2x = 6$
$x = \dfrac{6}{2}$
$x = 3$
So $x = 3$ is the only critical value of the given function. Moreover, the calculated critical value lies in the given interval $[0,4]$.
The absolute extremes of a function must occur at endpoints on the bounded interval (in this case, $0$ or $4$) or at the calculated critical values, so in this case, the points where the absolute extreme will occur are $0$, $4$, or $3$; hence we have to calculate the value of the given function at these points.
The value of $f(x)$ at $x = 0$
$f (0) = (0)^{2} – 6 (0) + 10 = 10$
The value of $f(x)$ at $x = 4$
$f (4) = (4)^{2} – 6 (4) + 8 = 16 – 24 + 10 = 2$
The value of $f(x)$ at $x = 3$
$f (3) = (3)^{2} – 6 (3) + 10 = 1$
The highest or maximum value is $10$ at $x = 0$ and the lowest or minimum value is $1$ at $x = 3$. With this, we can conclude that the maximum value of the given function is $10$, which occurs on the left end point at $x = 0$ while the minimum value occurs at the critical point $x = 3$.
Example 2:
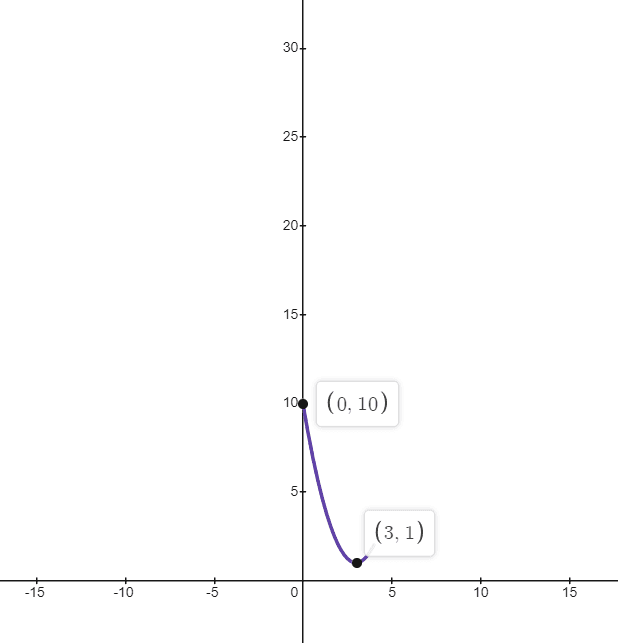
Find the extreme values for the function $f(x) = 2x^{3} – 6x^{2} + 8$ on the closed interval $[-2,5]$.
Solution:
$f(x) = 2x^{3} – 6x^{2} + 8$
$f'(x) = 6x^{2} – 12x$
$6x^{2} – 12x = 0$
$6x (x – 2) = 0$
So $x = 0$ and $x = 2$ are the critical values of the given function. Hence the maxima and minima of the given function will either be at the endpoints of the interval $[-2, 5]$ or at the critical points $0$ or $2$. Calculate the value of the function on all four points.
The value of $f(x)$ at $x = 0$
$f (0) = 2(0)^{3} – 6(0)^{2} + 8 = 8$
The value of $f(x)$ at $x = 2$
$f (2) = 2(2)^{3} – 6(2)^{2} + 8 = 16 – 24 + 8 = 0$
The value of $f(x)$ at $x = -2$
$f (-2) = 2(-2)^{3} – 6(-2)^{2} + 8 = -16 – 24 + 8 = -32$
The value of $f(x)$ at $x = 5$
$f (5) = 2(5)^{3} – 6(5)^{2} + 8 = 250-150+8 = 108$
The highest or maximum value is $108$ at $x = 5$ and the lowest or minimum value is $-32$ at $x = -2$.
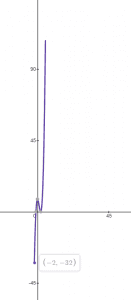
Example 3:
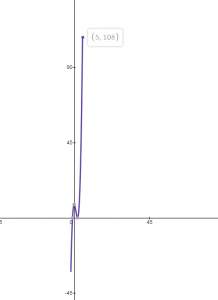
Find the extreme values for the function $f(x) = 8x^{3} – 12x^{2}$ on the closed interval $[0, 4]$.
Solution:
$f(x) = 8x^{3} – 12x^{2}$
$f'(x) = 24x^{2} – 24x$
$24x^{2} – 24x = 0$
$24x (x – 1) = 0$
So $x = 0$ and $x = 1$ are the critical values of the given function. Hence the maxima and minima of the given function will either be at the $0$, $2$, or $4$. Calculate the value of the function on all three points.
The value of $f(x)$ at $x = 0$
$f (0) = 8(0)^{3} – 12(0)^{2} = 0$
The value of $f(x)$ at $x = 1$
$f (1) = 8(1)^{3} – 12(1)^{2} = 8 – 12 = -4$
The value of $f(x)$ at $x = 4$
$f (4) = 8(4)^{3} – 12(4)^{2} = 512 – 192 = 320$
The highest or maximum value is $320$ at $x = 4$ and the lowest or minimum value is $-4$ at $x = 1$.
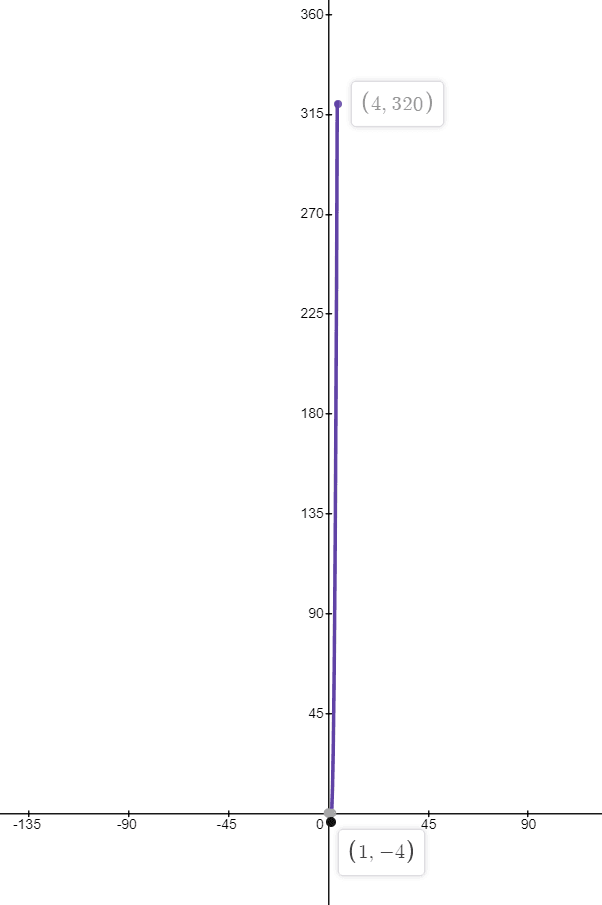
Example 4:
Find the extreme values for the function $f(x) = sinx^{2}$ on the closed interval $[-3,3]$.
Solution:
$f(x) = sinx^{2}$
$f'(x) = 2x cosx^{2}$
$2x cosx^{2} = 0$
$2x = 0$ and $cosx^{2} = 0$
$f'(x) = 0$ at $x = 0$, so one of the critical point is $x = 0$ while the rest of critical points where value $x^{2}$ is such that it makes $cosx^{2} = 0$. We know that $cos(x) = 0$ at $x = \pm\dfrac{\pi}{2}, \pm\dfrac{3\pi}{2}, \pm\dfrac{5\pi}{2}$…
So, $cosx^{2} = 0$ when $x = \pm\sqrt{\dfrac{\pi}{2}}, \pm\sqrt{\dfrac{3\pi}{2}}, \pm\sqrt{\dfrac{5\pi}{2}}$…
Hence the maxima and minima of the given function will either be at the endpoints of the interval $[-3, 3]$ or at the critical points $0$,$\pm\sqrt {\dfrac{\pi}{2}}$, $\pm\sqrt {\dfrac{3\pi}{2}}$ and $\pm\sqrt {\dfrac{5\pi}{2}}$.
Calculate the value of the function on all these points.
The value of $f(x)$ at $x = 0$
$f (0) = sin(0)^{2} = 0$
The value of $f(x)$ at $x = \sqrt{\dfrac{\pi}{2}}$
$f (\sqrt{\pi}) = sin(\sqrt{\dfrac{\pi}{2}})^{2} = 1$
The value of $f(x)$ at $x = -\sqrt{\dfrac{\pi}{2}}$
$f (-\sqrt{\pi}) = sin(-\sqrt{\pi})^{2} = 1$
The value of $f(x)$ at $x = \sqrt{\dfrac{3\pi}{2}}$
$f (\sqrt{\dfrac{3\pi}{2}}) = sin(\sqrt{\dfrac{3\pi}{2}})^{2} = -1$
The value of $f(x)$ at $x = -\sqrt{\dfrac{3\pi}{2}}$
$f (-\sqrt{\dfrac{3\pi}{2}}) = sin(-\sqrt{\dfrac{3\pi}{2}})^{2} = -1$
The value of $f(x)$ at $x = \sqrt{\dfrac{5\pi}{2}}$
$f (\sqrt{\dfrac{5\pi}{2}}) = sin(\sqrt{\dfrac{5\pi}{2}})^{2} = 1$
The value of $f(x)$ at $x = -\sqrt{\dfrac{5\pi}{2}}$
$f (-\sqrt{\dfrac{5\pi}{2}}) = sin(-\sqrt{\dfrac{5\pi}{2}})^{2} = 1$
The value of f(x) at $x = 3$
$f (0) = sin(3)^{2} = 0.412$
The value of $f(x)$ at $x = -3$
$f (0) = sin(-3)^{2} = 0.412$
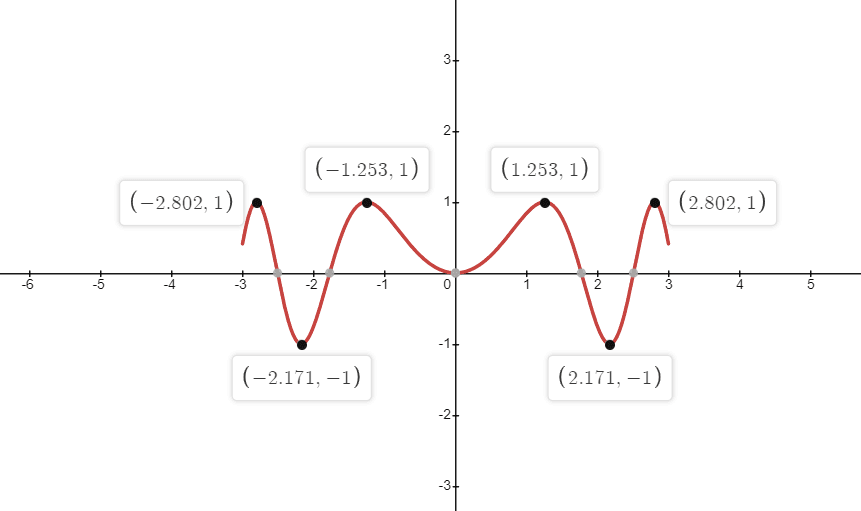
Important Definitions
Continuous Function
A function is known as a continuous function if the graph of the said function is continuous without any breakpoints. The function will be continuous on all the points of the given interval. For example, $x^{2}$, $x^{4}$, $\sqrt{x}$ are all continuous functions. Mathematically, a function $f(x)$ is continuous in $[a,b]$ if $\lim x \to c f(x) = f(c)$ for all $c$ in $[a,b]$.
The differentiation of a function can only be carried out if the function is continuous; the critical points of a function are found using differentiation. So to find the extreme values of a function, it is essential that the function must be continuous.
Closed Interval
A closed interval is an interval that includes all the points within the given limit, and square brackets denote it, i.e., [ ]. For example, the interval $[3, 6]$ includes all the greater and equal points to $3$ and less than or equal to $6$.
Practice Questions:
- Find the extreme values for the function $f(x) = 6x^{2} -3x +12$ on the closed interval $[0, 3]$.
- Find the extreme values for the function $f(x) = xe^{6x}$ on the closed interval $[-2, 0]$.
Answer Key:
1.
$f(x) = 6x^{2} -3x +12$
$f^{‘}(x) = 12x -3 $
$= 12x -3 = 0$
$x = \dfrac{1}{4}$
So $x = \dfrac{1}{4}$ is the critical value of the given function. Hence, the maxima and minima of the given function will either be at the $\dfrac{1}{4}$, $0$, or $3$.
Calculating the value of the function on all three points:
The value of $f(x)$ at $x = 0$
$f (0) = 6(0)^{2} – 3(0) +12 = 12$
The value of $f(x)$ at $x = 3$
$f (3) = 6(3)^{2} – 3(6) +12 = 54 – 9 + 12 = 57$
The value of $f(x)$ at $x = \dfrac{1}{4}$
$f (4) = 6(\dfrac{1}{4})^{2} – 3(\dfrac{1}{4}) +12 = \dfrac{3}{8}+\dfrac{3}{4}+ 12 = 13.125$
The highest or maximum value is $48$ at $x = 3$ and the lowest or minimum value is $12$ at $x = 0$.
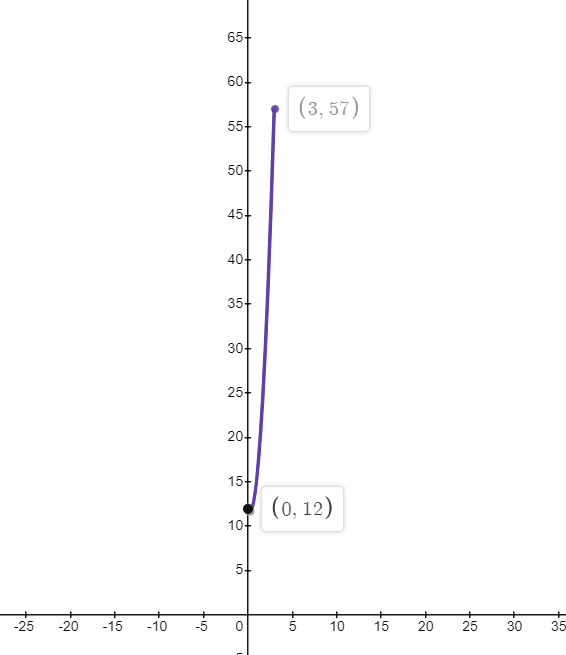
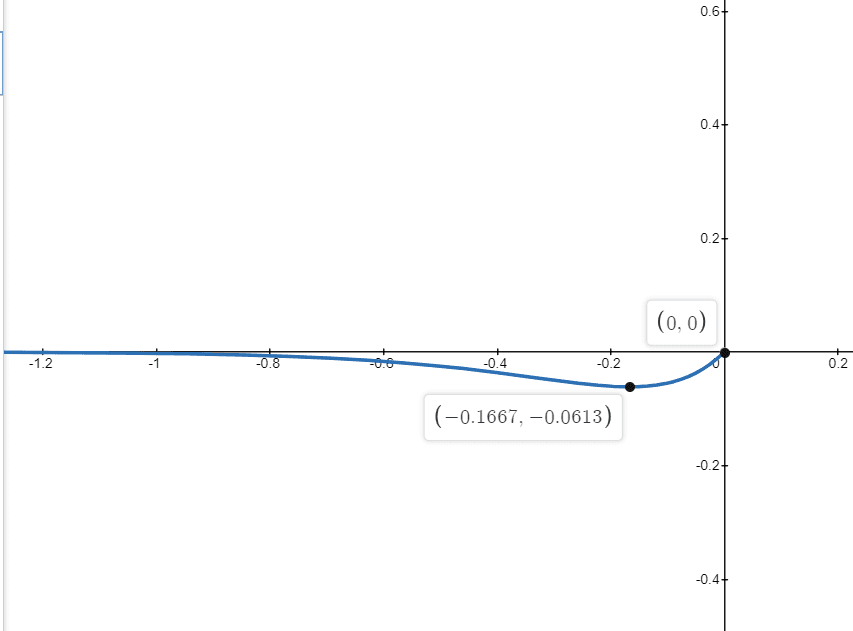
2.
$f(x) = xe^{6x}$
Applying chain rule to differentiate the above function:
$ f^{‘}(x) = 1. e^{6x} + 6x. e^{6x} = e^{6x}(1+6x)$
Now putting $f^{‘}(x) = 0$
$e^{6x}(1+6x) = 0$
$ 1+6x = 0$
$ x = – \dfrac{1}{6}$
So $x = -\dfrac{1}{6}$ is the critical value of the given function. Hence, the maxima and minima of the given function will either be at the $-\dfrac{1}{6}$, $-2$ or $0$.
Calculating the value of the function on all three points:
The value of $f(x)$ at $x = 0$
$f (0) = 0. e^{0} = 0$
The value of $f(x)$ at $x = -2$
$f (3) = -2. e^{-12} = -1.22 \times 10^{-5}$
The value of $f(x)$ at $x = -\dfrac{1}{6}$
$f (3) = -\dfrac{1}{6}. e^{-1} = 0.06131$