- Home
- >
- Square Roots – Explanation & Examples
JUMP TO TOPIC
Square Roots – Explanation & Examples
 In mathematics, a square root of a number x is such that, a number y is the square of x, simplify written as y2 = x.
In mathematics, a square root of a number x is such that, a number y is the square of x, simplify written as y2 = x.
For example, 5 and – 5 are both square roots of 25 because:
5 x 5 = 25 and -5 x -5 =25.
The square root of a number x is denoted with a radical sign √x or x 1/2. For instance, the square root of 16 is presented as: √16 = 4. A number whose square root is calculated is referred to as radicand. In this expression, √16 = 4 number 16 is the radicand.
What is a Square Root?
Square root is an inverse operation of the squaring a number. In other words, square root is an operation that undoes an exponent of 2.Properties
- A perfect square number has a perfect square root.
- An even perfect number has the square root that is even.
- Odd perfect number has the square root that is odd.
- The square root of a negative number is undefined.
- Only numbers ending with even number of zeros have square roots.
How do we find square root of numbers?
There are multiple ways to find the square of the numbers. We will see a few of the here.
Repeated Subtraction
This method involves, successful and repeated subtraction of odd numbers such as 1, 3, 5 and 7 from the number until zero is reached. The square of the number is equal to the number or frequency of subtraction performed on the number
Suppose, we need to calculate the square of a perfect number like 25, the operation is done as:
| 25 -1 | = 24 |
| 24 -3 | = 21 |
| 21 -5 | = 16 |
| 16 – 7 | = 9 |
| 9 – 9 | = 0 |
You can notice that, the frequency of subtraction is 5, therefore the square root of 25 is 5.
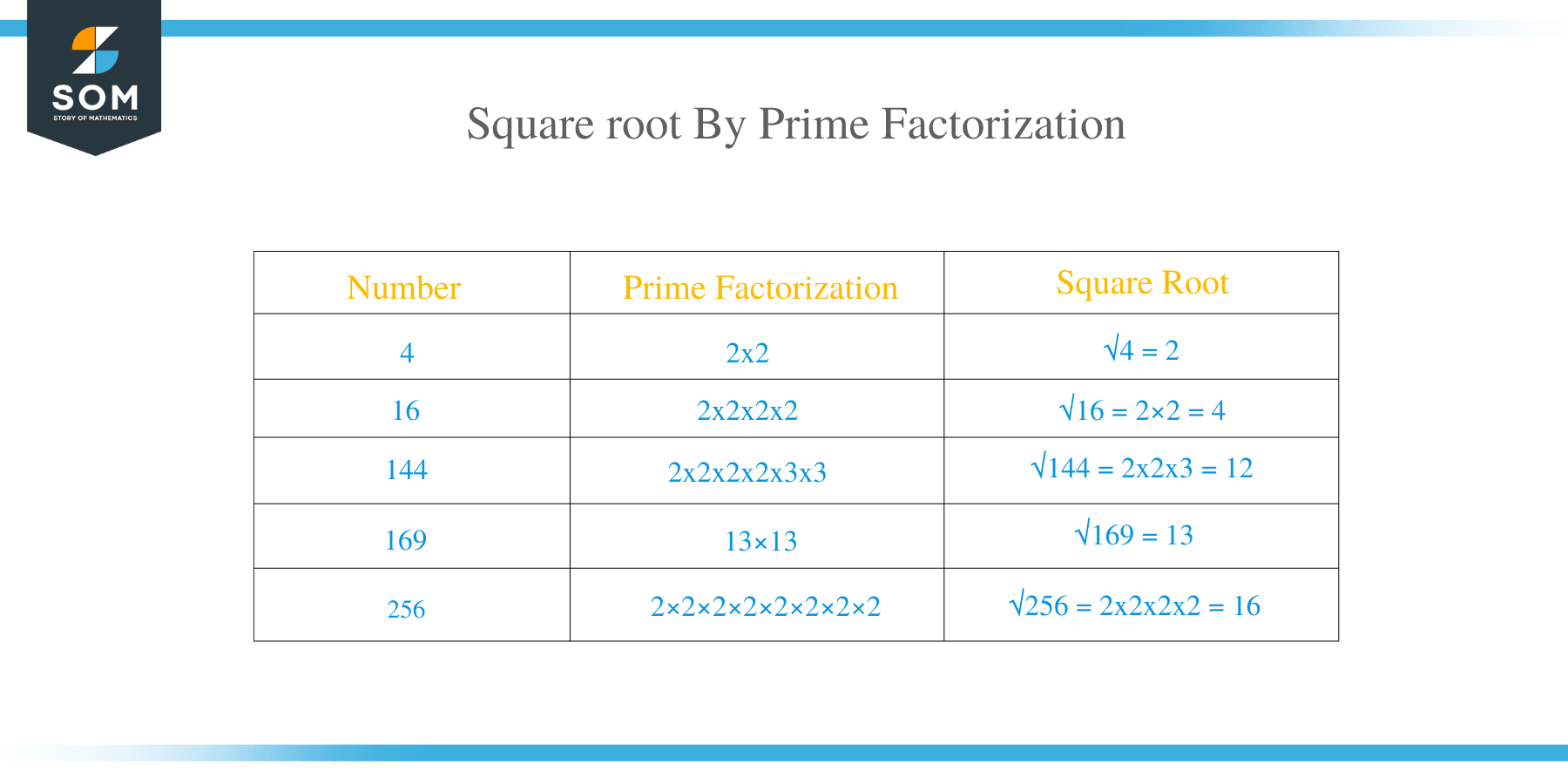
Prime Factorization
In this method, a perfect square number is factorized by successive division. The prime factors are grouped into pairs, and the product of each number calculated. The product is therefore, the square root of the number. To find the square of a perfect number such as: 144 is performed as:
- 144 = 2 × 2 × 2 × 2 × 3 × 3.
- Pair the prime factors.
- Selecting one number from each pair.
- 2 × 2 × 3 = 12.
- Thus, the √144 = 12.

Division Method
Division method is a suitable technique of calculating the square of a large number. The following are the steps involved:
- A bar is placed over every pair of digits starting from the right-hand side.
- Divide left end number by a number whose square is less or equivalent to the numbers under the left end.
- Take this number as the divisor and quotient. Similarly, take the leftmost number as the dividend
- Divide to get the result
- Pull down the next number with a bar to the right-hand side of the remainder
- Multiply the divisor by 2.
- To the right of this new divisor, find a suitable dividend. This process is repeated until we get zero as the remainder. The square of the number therefore is equal to the quotient.
The square root of 225 is calculated as
- Begin the division from the leftmost side.
- In this case, 1 is our number whose square is below 2.
- Assigning 1 as the divisor and quotient and multiplying it by 2, gives:
- Proceed with the steps to get 15 as the quotient.
Square Roots – Complete List
Below is the list of Square Roots of various numbers. The solution is just one click away.
Square Root Of 123
Square Root Of 200
Square Root Of 24
Square Root Of 28
Square Root Of 89
Square Root Of 52
Square Root Of 288
Square Root Of 625
Square Root Of 8
Square Root Of 256
Square Root Of 121
Square Root Of 225