- Home
- >
- Vectors
Vectors
No, they’re not just arrows.
And no, they’re not rays.
Vectors are mathematical elements used to represent an entity with both direction and magnitude.
They are drawn to look similar to a ray since vectors are usually represented as a line segment with an endpoint on one side and an arrow on the other.
Unlike rays, however, vectors have a definite length, which represents their magnitude. The arrow, rather than symbolizing that the vector continues indefinitely, indicates the direction of the vector in a way that a regular line segment could not.
Vector mathematics uses some of the concepts from topics such as geometry and algebra to define vector spaces. The topic itself, however, has many applications in physics.
For example, velocity is different from speed because it has a direction, usually indicated by a positive or negative sign when represented algebraically. A mathematical approach to vectors will often include the coordinate plane and geometric concepts, but physics usually separate the concept from specific locations.
This resource guide introduces vectors from a mathematical perspective. It begins by explaining vectors generally and how vector operations work. The first topic also includes information on geometric representations of vectors. The second topic relates vectors to parametric equations since both concepts can be used to describe motion.
It begins by showing different strategies for vector operations. It then explains how vectors can be used to represent forces. The section uses this information to define the relationship between parametric equations and vectors.
The topic ends by generalizing vectors in two dimensions to vectors in three dimensions.
Vector Introduction
When represented geometrically, the length of the vector indicates its magnitude and the angle represents its direction. Unlike regular geometric elements, however, operations can be performed on vectors in much the same way they are performed on regular numbers, functions, and even matrices. For example, it is possible to add and subtract vectors as well as multiply them by a scalar.

The image illustrates the intuitive concept behind vector addition by showing the sum of a red and blue vector as a purple vector. Though it may not match up with many people’s idea of a sum, it makes sense in light of forces in physics.
This guide first explains vectors and what it means for a vector to have magnitude. It then goes on to explain the vector operations of addition, subtraction, and scalar multiplication.
The topic finishes by explaining parallel vectors, vector geometry, and position vectors.
- What is a Vector?
- Vector Magnitude
- Equal Vectors
- Negative Vectors
- Vector Addition
- Vector Subtraction
- Multiplication by a Scalar
- Parallel Vectors
- Vector Geometry
- Position Vector
Vectors and Parametric Equations
Vectors are usually drawn as an arrow, and this geometric representation is more familiar to most people. They can, however, also be represented algebraically by giving a pair of coordinates.
Typically, this is done by assuming the vector has an endpoint at (0,0) on the coordinate plane and using a method similar to finding polar coordinates to find the direction and magnitude. For example, a vector represented by the coordinates (3, 0) points directly to the right and has a magnitude of 3.
This section also deals with why vector operations work and how they can be generalized outside of the coordinate plane, especially in physics scenarios.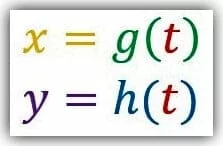
Parametric equations, where the x variable depends on a third variable, can be used to gain insights about vectors. Since x depends on a third variable, t, x is written as a function of t. Consequently, y is considered a function of both x and t. Parametric equations are great for describing motion as vectors are great for describing forces.
Finally, most of the discussion of vectors in this guide has dealt with vectors in two dimensions. In applications, however, three-dimensional vectors are quite common.
These resources for this topic begin by explaining the differences between geometric and algebraic representations of vectors and how these relate to vector operations. It then explains in greater detail how vectors are used to represent forces in physics. The next part deals with the relationship between parametric equations and vectors.
Finally, the topic concludes with the explanation of three-dimensional vectors.
