JUMP TO TOPIC
Coinciding Lines – Explanation and Examples
Maths is all about numbers and graphs, and graphs are practically non-existent without incorporating some lines and curves. Not only do these lines and curves depict information regarding a problem under study, but they also help the mathematician to resolve complex problems by simply tracing the desired points on the curves or lines.
When it comes to lines, 3 kinds of lines are the most significant; parallel, perpendicular, and coinciding. In this section, we will be covering coinciding lines, which are defined as:
“The lines which lie exactly on top of one another such as they appear as one are defined as coinciding lines.”
In this section, we will be covering the following topics:
- What are coincident lines?
- What is the formula of coinciding lines?
- How to check if the lines are coincident or not?
- Examples
- Practice problems
What Are Coincident Lines?
Coinciding lines are basically 2 lines that completely lie on one another. There are neither parallel nor perpendicular but are completely identical. When such lines are graphed, they appear as one, as shown in the figure below.
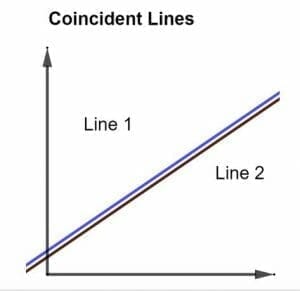
Although it may seem that there appears to be only one line, that is not the case. When drawn together, the two lines, one red and one blue appear as one line since these 2 lines are coinciding in nature.
In the world of mathematics, multiple lines and curves exist. Some are oblique, some are parallel, some are perpendicular, or some may bend into a curve and form shapes like parabolas and ellipses. Among all these lines and curves enveloping fundamental mathematics concepts, specifically in geometry, coinciding lines hold special importance.
Unlike parallel lines, which never intersect, and perpendicular lines directed at 90𝆩 to one another, coinciding lines are entirely different.
Coinciding lines do not vary in terms of either magnitude or direction. When we term them as ‘identical,’ it implies exactly that.
Some concepts may often result in confusion between parallel and coinciding lines since both are directed in the same direction, but that is not the case. Parallel lines, though they may be directed in the same direction, cut the y-axis on different points. However, in coinciding lines, since they are already termed as ‘identical,’ they cut the y-axis on the same points. We can validate this concept from the figure below:
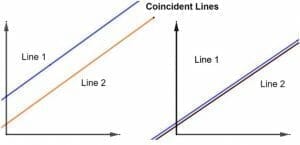
So, the major difference in parallel and coinciding lines lies in the determination of their intercept. This concept is explained below:
The Intercept of Coinciding Lines
Let’s cover the concept of intercept first before jumping into the intercepts of coincident lines.
Intercept is defined as the point where a line cuts the x or y-axis. Every line has an intercept, which can either be obtained by extending the particular line or simply graphing the desired line equation.
The intercept can exist on all axes depending on the coordinate system the lines are being graphed in. In the case of two-dimensional, we only have 2 said axes, namely the x and y-axis. So, in the two-dimensional system, only 2 possible intercepts can exist, one on the x-axis and the other on the y-axis.
In the case of three-dimensional, a new axis, the z-axis, exists. So in the three-dimensional plane, 3 possible intercepts can exist; one on the x-axis, one on the y-axis, and one on the z-axis.
Now let’s analyze the concept of intercept in the coinciding lines. We mentioned earlier that the major difference in parallel and coinciding lines lies based on their intercept, so let’s evaluate that.
The coinciding lines are identical lines that fall exactly on top of one another and cut the respective axis on the same points. So, all the coinciding lines have the same intercept, whether on the x-axis or the y-axis. This means that the difference of the intercept between the said coinciding lines is always zero since the said lines have the same intercept.
So, if you ever get confused between parallel lines and coinciding lines, check for their intercept difference. Parallel lines never intersect one another and hence will always have different intercepts. In comparison, coinciding lines are entirely identical and lie on top of one another and hence will have the same intercept, resulting in zero intercept difference between the lines.
Formula Of Coinciding Lines
For coinciding lines, we can apply the following more specific formula from the generic equation of a straight line.
ax + by = c
Where ‘a’ and ‘b’ are the constants of the variables x and y, and ‘c’ is the intercept.
To evaluate the formula for coinciding lines, we will first analyze the formula of a straight line. The formula of a straight line is quite simple and is stated below:
y = mx + b
Where ‘m’ is the slope of the respective line, and ‘b’ is the line’s intercept on any particular axis.
This equation can be implied on any straight line, including parallel lines. For parallel lines, the particular lines would have the same slope ‘m’ but different intercepts ‘b.’
Now let’s consider the coinciding lines,
We have already mentioned above that the coinciding lines are identical and hence would have the same slope. We have also discussed that the coinciding lines have the same intercepts on any particular axis. So if we analyze the above equation for a straight line, we can directly state that the variables ‘m’ and ‘b’ in coinciding lines are identical.
How To Check If The Lines Are Coinciding?
One method for checking whether the lines are coincident is the intercept method, and the other is with the help of the coinciding line equation.
Now that we have covered the concept of what coinciding lines are and how they are different from lines such as parallel lines, let’s evaluate whether the pair of lines coincide.
One method for checking whether the lines coincide or not has already been discussed above. In that discussed method, we check for the intercept difference. If the intercept difference between two or more lines is zero, then the lines are entitled to be coinciding. However, this method is more commonly used to differentiate between parallel and coinciding lines and not exactly tells us how to check whether the lines coincide or not.
To check for the coinciding lines, we will consider the following formula:
ax + by = c
The above formula of the linear equation for coinciding lines can also be written as below:
ax + by + c = 0
Now, consider that we actually have 2 linear lines. The coinciding line equation for each line can be written as below:
For line 1:
a1x + b1y = c1
For line 2:
a2x + b2y = c2
Since coinciding lines are completely identical, such lines have all the common points between them. Now, to check whether 2 lines are coinciding or not, we will rearrange the above formulas for each line in the following manner such that we will be dividing the equation of line 2 with the equation of line 1. Upon dividing and evaluating the equations, we obtain the following result:
a1/a2 = b1/b2 = c1/c2
If this equality prevails, the lines are said to be coincident.
Hence, this pair of lines are said to be coincident, and they would be having an infinite number of solutions. This concept can be strengthened and proved with the help of examples.
Example 1
Check whether the following pair of lines are coincident or not:
x + y = 3 2x + 2y = 6
Solution
We will be making use of the following equation to determine whether the said pair of lines are coinciding or not.
a1/a2 = b1/b2 = c1/c2
From equation 1, it can be written:
x + y = 3
a1 = 1 b1 = 1 c1 = 3
Similarly, from equation 2 it can be written:
2x + 2y = 6
a2 = 2 b2 = 2 c2 = 6
Now, let’s apply the formula:
a1/a2 = 1/2
Also,
b1/b2 = 1/2
And similarly,
c1/c2 = 3/6
c1/c2 = 1/2
Hence, it is proved:
a1/a2 = b1/b2 = c1/c2
1/2 = 1/2 = 1/2
Since the equation is satisfied, hence the given pair of lines are coinciding lines.
Example 2
Validate whether the following pair of lines are coincident or not:
9x – 2y + 16 = 0 18x – 4y + 32 = 0
Solution
We will be making use of the following equation to determine whether the said pair of lines are coinciding or not.
a1/a2 = b1/b2 = c1/c2
From equation 1, it can be written:
9x – 2y + 16 = 0
a1 = 9 b1 = -2 c1 = 16
Similarly, from equation 2 it can be written:
18x – 4y + 32 = 0
a2 = 18 b2 = -4 c2 = 32
Now, let’s apply the formula:
a1/a2 = 9/18
a1/a2 = 1/2
Also,
b1/b2 = -2/-4
b1/b2 = 1/2
And similarly,
c1/c2 = 16/32
c1/c2 = 1/2
Hence, it is proved:
a1/a2 = b1/b2 = c1/c2
1/2 = 1/2 = 1/2
Since the equation is satisfied, hence the given pair of lines are coinciding lines.
Example 3
Confirm whether the following pair of lines are coincident or not:
2x + 3y + 1 = 0 2x + 7y + 1 = 0
Solution
We will be making use of the following equation to determine whether the said pair of lines are coinciding or not.
a1/a2 = b1/b2 = c1/c2
From equation 1, it can be written:
2x + 3y + 1 = 0
a1 = 2 b1 = 3 c1 = 1
Similarly, from equation 2 it can be written:
2x + 7y + 1 = 0
a2 = 2 b2 = 7 c2 = 1
Now, let’s apply the formula:
a1/a2 = 2/2
a1/a2 = 1
Also,
b1/b2 = 3/7
And similarly,
c1/c2 = 1/1
c1/c2 = 1
As,
a1/a2 ≠ b1/b2 ≠ c1/c2
Hence, the given pair of lines are not coinciding lines.
Practice Problems
- Check whether the pair of lines are coincident or not: x + y = 0 3x + 3y = 0
- Confirm if the following pair is coincident or not: 12x + 4y + 14 = 0 36x + 12y + 42 = 0
- Confirm if the following pair is coincident or not: 8x + 15y + 7 = 0 54x + 3y + 2 = 0
Answers
- Yes
- Yes
- No
All the images are constructed using GeoGebra.