Pre-Calculus

Pre-calculus is of a hodgepodge of different mathematical concepts. In most high school courses, it is combined with trigonometry, and even its name is dependent on another subject, calculus. Pre-calculus tends to encompass any gaps in knowledge that should be filled in before the study of calculus.

The topics that most distinctly belong to pre-calculus are graph transformations and conic sections, and this tends to be the focus of most courses. The subject also tends to cover logarithms, polynomials, and exponential functions. Typically, pre-calculus will provide an introduction to complex numbers, vectors, and polar coordinates as well.

This guide begins with an explanation of graph transformations and polynomials, which are used to then explore conic sections. The guide also includes information on logarithmic, exponential, and rational functions.

Finally, it provides introductions to the topics of complex numbers, vectors, polar coordinates, and sequences before finishing up with an exploration of advanced topics in trigonometry.

Functions and Transformations of Graphs

Changes to the algebraic form of a function cause predictable changes to a graph. Likewise, a change in a graph causes predictable changes to the algebraic form of a function.

These two facts are useful for any job that involves drawing up blueprints or making prototypes, including architecture, engineering, and even art.

This section begins by explaining the domain of a function and a few special types of functions. It then uses these facts to explain different types of transformations on functions, including translations, stretches, compressions, and reflections.

Finally, the section ends with a discussion of one-to-one functions and their inverses.

Polynomials

Any expression with at least one variable is considered a polynomial. Polynomial functions usually consist of the sum of different powers of the same variable multiplied by constants.

This topic discusses polynomial functions and their graphs. It then goes on to explain how to find the equation based on a graph before discussing characteristics of functions, including maxima, minima, intercepts, and reciprocals.

Conic Sections

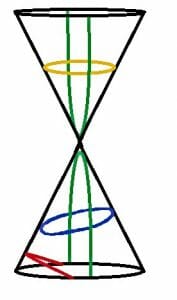
Conic sections correspond to the different graphs of functions where the x and y variables are squared.

There are four different kinds of conic sections:
circles, ellipses, parabolas, and hyperbolas.

These functions are called conic sections because they correspond to the cross sections of different cuts on a cone.

The topic begins by introducing the four different conic sections and then explaining how to graph them.

Exponential Functions

Exponential functions are functions where the variable is an exponent of a constant base.

This topic introduces exponential functions and their graphs. It then explains how to solve exponential functions with the same and different bases.

Logarithmic Functions

If subtraction is the opposite of division, then logarithmic functions are the opposite of exponential functions. In these equations, the base of the logarithm is constant, and the variable is the “argument” of the log.

The natural log, which has base e, is the most commonly used logarithm.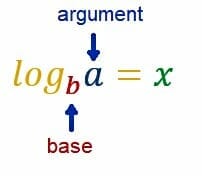

This section begins by introducing logarithmic functions and explaining their relationship to exponential functions.

It also explains how to work with these functions, including how to both expand and simplify them.

Rational Functions

Rational functions include at least one term that has a variable in the denominator. They can thus be written as one numerator over one denominator.

This topic explains rational functions and their limits. It then uses this information to explore graphing rational functions, including how to graph limits as asymptotes.

Finally, the section ends with a discussion of discontinuous rational functions.

Complex Numbers

Many people would argue that all numbers are complex!

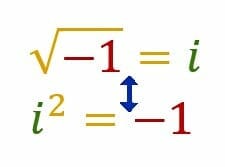The term, however, refers to any number that includes the square root of -1, denoted by i. This is because another term for complex numbers is “imaginary numbers.” This name tends to cause confusion, however, so “complex” is used more frequently.

This topic gives an introduction to complex numbers and how basic operations with complex numbers work. It also explains how to work with both complex and non-complex numbers at the same time by exploring the polar form of writing complex numbers.

Finally, the topic concludes with a section on how to find roots and simplify complex rational expressions.

Vectors and Parametric Equations

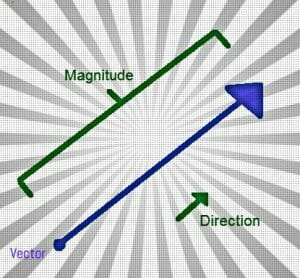
Vectors are lines with both direction and magnitude, and they are frequently used in physics. Parametric equations are ones where the variable depends on another variable. Parametric equations can be used as another way to describe functions.

This section explains both geometric and algebraic representations of vectors and their components. It then goes over how to use basic operations with vectors.

The subtopics on vectors conclude with an overview of unit vectors and the vector equation of a line.

The topic then briefly explains parametric equations and how to use them.

Polar Coordinates

Polar coordinates are a different way of representing points and lines in a plane. Typically, one uses the x-value of a pair of coordinates to figure out how far to the left or right to go, and they use the y-value of a pair of coordinates to determine the height.

In polar coordinates, however, one number gives an angle from the horizontal and the other gives the length of a line. Polar coordinates are helpful for graphing different curves, including circles and spirals. It is easy to use polar coordinates to graph rounded shapes such as circles and spirals.

This topic gives an overview of polar coordinates by first explaining them and their relationship to rectangular coordinates.

It also explains how equations work in polar coordinates, including how to recognize symmetry and make graphs of functions.

Sequences and Series

Sequences and series tend to reappear in calculus II, and knowing how to write out a sequence can be a useful skill. This topic gives a very brief overview of sequences, including arithmetic, geometric, and recursion sequences.

Advanced Trigonometry

The subject of pre-calculus ends by exploring a few more in-depth topics relating to trigonometry, especially since the two subjects are often taught in tandem.

This sections mainly deals with inverse trigonometric functions, strategies for factoring them, and advanced trigonometric identities.