- Home
- >
- One sided limits – Definition, Techniques, and Examples
JUMP TO TOPIC
One sided limits – Definition, Techniques, and Examples
 What happens when the graph of a function contains discontinuities such as piecewise and rational functions? The function’s behavior may differ as the function approaches from the left or the right, so we instead inspect its one-sided limits.
What happens when the graph of a function contains discontinuities such as piecewise and rational functions? The function’s behavior may differ as the function approaches from the left or the right, so we instead inspect its one-sided limits.
One-sided limits are the function’s limits as they approach a restricted value or side of the function.
This article will review discontinuities and how they affect the graph’s limit as it approaches from the left or right of $x = a$. We’ll also introduce you to the techniques of finding the limits of a function from the left and from the right.
What is a one sided limit?
A one-sided limit can either be of the form $\lim_{x \rightarrow a^{-}} f(x)$ or $\lim_{x \rightarrow a^{+}} f(x)$. The plus or minus sign following $a$ indicate the region or interval that we want to observe.
From the notations alone, we can see that one-sided limits are the limits of the function as it approaches a certain value and interval.
One-sided limits are helpful when we want to check for discontinuities and if we want to confirm if a limit exists. Let’s observe the piecewise function, $f(x)=\left\{\begin{matrix}x,&x < 0\\ 5 – x,&x \geq 0\end{matrix}\right.$, and the behavior of $x$ as it approaches $0$.

This piecewise function is a good example of why we study one-sided limits. As $x$ approaches $0$ from the left, we can see that the limit of $f(x)$ is equal to $0$, and when $x$ approaches $0$ from the right, the limit becomes $5$.
This shows that it is possible for the limit from each side of the function may be different.
What does the limit from the left mean?
Let’s dive into understanding what $\lim_{x \rightarrow a^{-}} f(x)$ represent. When we see $\lim_{x \rightarrow a^{-}}$ , this means that the limit is evaluated from the left of $a$.
When we say limit from the left of $a$, we want to find the limit of $f(x)$ as $x<a$ without letting $x$ be $a$.
For the piecewise function, $f(x)=\left\{\begin{matrix}x,&x < 0\\ 5 – x,&x \geq 0\end{matrix}\right.$, $\lim_{x \rightarrow 0^{-} }f(x)$ represents the limit of the function as $x$ approaches zero coming from the values that are less than 0.
What does the limit from the right mean?
Similarly, whenever we see $\lim_{x\rightarrow a^{+} }$, this means that the limit is evaluated from the right of $a$ or when $x<a$ without letting $x$ be $a$.
Using the same example, $f(x)=\left\{\begin{matrix}x,&x < 0\\ 5 – x,&x \geq 0\end{matrix}\right.$, $\lim_{x \rightarrow 0^{+}} f(x)$ represents the limit of $f(x) as $x$ approaches zero coming from the values that are greater than 0.
How to find one sided limits?
Since the only difference between one-sided and regular limits are the intervals we’re working with, make sure to review your knowledge on evaluating limits as we might need some of the techniques to find one-sided limits as well.
Finding one-sided limits from a graph
We can find either $\lim_{x \rightarrow a^{-}} f(x)$ or $\lim_{x \rightarrow a^{+}} f(x)$ by inspecting the graph’s behavior when $x < a$ or when $x > a$, respectively.
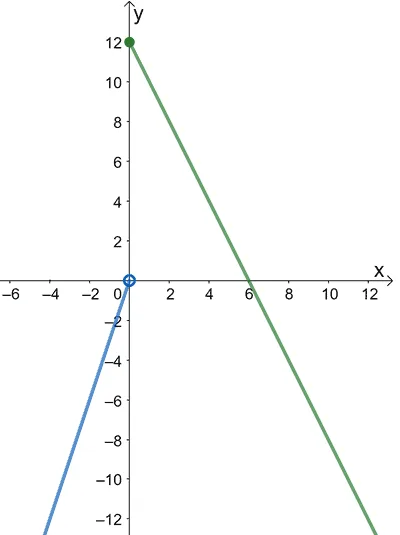
The graph of the piecewise function, $f(x)=\left\{\begin{matrix}3x,&x < 0\\ 12 – 2x,&x \geq 0\end{matrix}\right.$, is as shown above.
If we want to find $\lim_{x \rightarrow 0^{-}} f(x)$, we’ll look at the value that the interval $x<0$ approaches. Looking at the graph, we can see that from the left of $0$, the value approaches $0$.
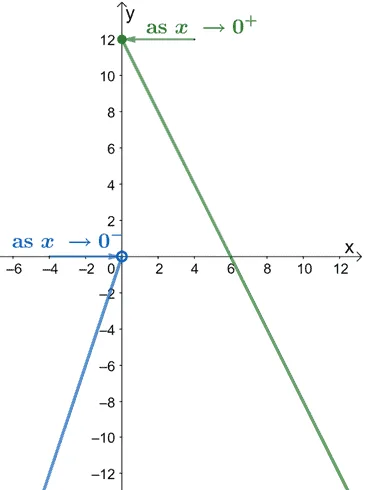
Similarly, to find $\lim_{x \rightarrow 0^{+}} f(x)$, let’s inspect the value of $f(x)$ that the values to the right of $0$ approach. The graph shows that the limit from the right would be equal to $12$ instead.
Finding one-sided limits algebraically
When given the expression for the function, and you need to find the limit as $x$ approaches $a$ from the left or $a$ from the right, it helps to keep in mind which values are being satisfied given a certain interval.
- Check which of the expressions will the values of $x<a$ belong to.
- Evaluate the limits at $x = a$ and for the corresponding expression of the function.
Let’s try finding $\lim_{x \rightarrow 2^{-}} f(x)$ and $\lim_{x \rightarrow 2^{+}} f(x)$ given the piece function, $f(x)=\left\{\begin{matrix}-x^2,& 0 \leq x\leq 2\\ 2x+ 1,&2 <x\leq 4\end{matrix}\right.$.
If we want to find the limit from the left or $\lim_{x \rightarrow 2^{-}} f(x)$, first check which of the two expressions would we be using for values that are from the left of $2$?
$f(x)=\left\{\begin{matrix}\color{blue}-x^2,& \color{blue}0 \leq x \leq 2\\ 2x + 1,&2 < x \leq 4\end{matrix}\right.$
We can see that we have $f(x) = -x^2$ when we want the values from the left of $2$, so $\lim_{x \rightarrow 2^{-}} f(x) = \lim_{x \rightarrow 2^{-}} –x^2$. Since $-x^2$ is a polynomial, we simply substitute $x=-2$ into $-x^2$.
$\begin{aligned}\lim_{x \rightarrow 2^{-}} f(x)&= f(2), \text{where } f(x) = -x^2\\ &= -(2)^2\\&=-4 \end{aligned}$
We can apply the same thought process for finding the value of $\lim_{x \rightarrow 2^{-}} f(x)$.
$\begin{aligned}\lim_{x \rightarrow 2^{+}} f(x)&= f(2), \text{where } f(x) = 2x + 1\\ &= 2(2) + 1\\&= 5 \end{aligned}$
This means that the limit of $f(x)$ from the left is $-4$ while the limit of $f(x)$ from the right is $5$.
How to find confirm if a function has a regular limit?
When we have $\lim_{x \rightarrow a^{-}} f(x)$ and $\lim_{x \rightarrow a^{+}} f(x)$, we can also confirm if a regular limit or $\lim_{x \rightarrow a} f(x)$ exists.
Let’s say $\lim_{x \rightarrow a^{-}} f(x) = M$ and $\lim_{x \rightarrow a^{+}} f(x) = N$, the function $f(x)$ has a regular limit if and only if $M = N$.
Summary of one sided limits definition and properties
Before we try out more problems that involve one-sided limits, why don’t we go ahead and recap everything that we’ve learned so far?
- When we’re looking for $\lim_{x \rightarrow a^{-}} f(x)$, this means that we want to see the values that $f(x)$ approaches from the left of $a$.
- Similarly, $\lim_{x \rightarrow a^{+}} f(x)$, means that we want to see the values that $f(x)$ approaches from the right of $a$.
- Regardless of what’s given to represent $f(x)$ (graphically, tabular, or its expression), always go back to the fundamental definition of one-sided limits.
Example 1
The graph of $f(x)$ is as shown below.
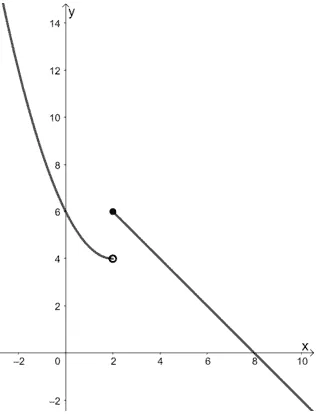
Determine the values of the following:
a. $\lim_{x \rightarrow 2^{-}} f(x)$
b. $\lim_{x \rightarrow 2^{+}} f(x)$
Solution
When working with one-sided limits, make sure that we’re working with the right intervals or side.
For $\lim_{x \rightarrow 2^{-}} f(x)$, we want to observe how $f(x)$ behaves based on the values to the left of $2$.
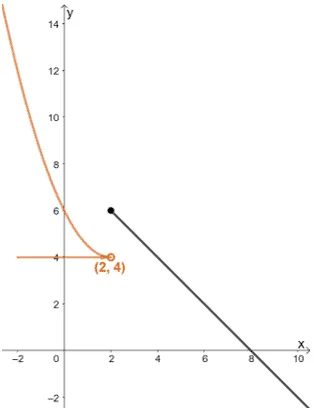
We can see that from the left, $x$ approaches $2$, the graph is approaching $4$.
a. This means that $\lim_{x \rightarrow 2^{-}} f(x) = 4$.
Inspecting the graph’s behavior from the right this time, we can see that as $x$ approaches $2$ from the right, the graph approaches $f(x) = 6$.
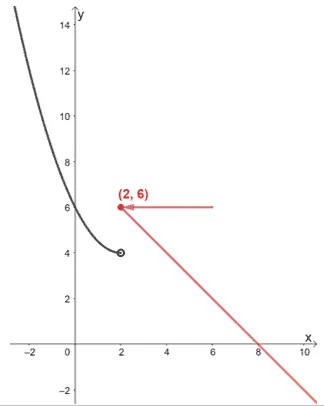
b. This means that $\lim_{x \rightarrow 2^{+}} f(x) = 6$.
Example 2
Describe the one-sided limits as $x$ approaches $4$ using the table of values for $f(x)$ as shown below.
| $\boldsymbol{x}$ | $\boldsymbol{f(x)}$ | $\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
| $3$ | $12.35789$ | $4.0001$ | $7.999999$ |
| $3.5$ | $12.45687$ | $4.001$ | $7.894725$ |
| $3.9$ | $12.65489$ | $4.01$ | $7.611480$ |
| $3.99$ | $12.78954$ | $4.1$ | $7.421597$ |
| $3.999$ | $12.96154$ | $4.5$ | $7.14057$ |
| $3.9999$ | $12.99999$ | $5$ | $7.01245$ |
Solution
When given the table of values, divide the group to have a table that shows all values of $x$ that are less than $4$ and a group where $x$ are all greater than $4$.
Why don’t we inspect the limit from the left of $f(x)$ as $x$ approaches $4$?
| $\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
| $3$ | $12.35789$ |
| $3.5$ | $12.45687$ |
| $3.9$ | $12.65489$ |
| $3.99$ | $12.78954$ |
| $3.999$ | $12.96154$ |
| $\color{blue} 3.9999$ | $ \color{blue} 12.99999$ |
We can see from the table that from the left, as $x$ approaches $4$, the value of $f(x)$ gets closer to $13$. This means that the value of $\lim_{x \rightarrow 4^{-}} f(x)$ is $13$.
We apply a similar approach but this time, we’re looking at the values of $x$ that are greater than $4$.
| $\boldsymbol{x}$ | $\boldsymbol{f(x)}$ |
| $\color{blue} 4.0001$ | $\color{blue} 7.999999$ |
| $4.001$ | $7.894725$ |
| $4.01$ | $7.611480$ |
| $4.1$ | $7.421597$ |
| $4.5$ | $7.14057$ |
| $5$ | $7.01245$ |
We can see that as $x$ gets closer to $4$ from the right, the value of $f(x)$ approaches $8$. Hence, we have $\lim_{x \rightarrow 4^{+}} f(x) = 8$.
Example 3
The function $f(x)$ is a piecewise function as shown by the equation below.
$ f(x)=\left\{\begin{matrix}\dfrac{x}{x+1},& 0 \leq x < 1\\ \sqrt{25-x^2},&1 \leq x \leq 5\\4x – 5,&5 < x \leq 10\end{matrix}\right.$
Evaluate the following expressions:
a. $\lim_{x \rightarrow 1^{-}} f(x)$
b. $\lim_{x \rightarrow 1^{+}} f(x)$
c. $\lim_{x \rightarrow 3^{-}} f(x)$
d. $\lim_{x \rightarrow 3^{+}} f(x)$
Use the result from a to d to confirm if there is a regular limit for $f(x)$ as $x$ approaches $1$ and when $x$ approaches $2$.
Solution
To find the limit of $f(x)$ as $x \rightarrow 1^{-}$, we can find its limit by using the right expression for $f(x)$ at when $ x< 1$.
$f(x)=\left\{\begin{matrix}\color{blue}\dfrac{x}{x-1},& \color{blue}0 \leq x < 1\\ \sqrt{25-x^2},&1 \leq x \leq 5\\4x – 5,&5 < x \leq 10\end{matrix}\right.$
When $0 \leq x < 1$, $f(x) = \dfrac{x}{x + 1}$, so find the value of $f(1)$ using the expression of $f(x)$ at the given interval.
$\begin{aligned} \lim_{x \rightarrow 1^{-}} f(x) &= f(1), {\text{ where }} f(x) &= \dfrac{x}{x + 1}\\&=\dfrac{\color{blue} 1}{{\color{blue}1} + 1}\\&= \dfrac{1}{2}\end{aligned}$
a. We now have $\lim_{x \rightarrow 1^{-}} f(x) = \dfrac{1}{2}$.
Applying the same process for the limit from the right of $1$. This time though, we have $f(x) = \sqrt{25 – x^2}$ when $1 \leq x \leq 5$.
$\begin{aligned} \lim_{x \rightarrow 1^{+}} f(x) &= f(1), {\text{ where }} f(x) &= \sqrt{25 – x^2}\\&=\sqrt{25 -{\color{blue}1}^2 }\\&= \sqrt{24}\\&= 2\sqrt{6}\end{aligned}$
b. Hence, we have $\lim_{x \rightarrow 1^{+}} f(x) = 2\sqrt{6}$.
We will apply the same thought process for parts c and d.
| Limit from left, $\boldsymbol{\lim_{x \rightarrow 3^{-}} f(x)}$ | Limit from right, $\boldsymbol{\lim_{x \rightarrow 3^{+}} f(x)}$ |
The values from the left of $3$ lies within $1 \leq x \leq 5$. $\begin{aligned} \lim_{x \rightarrow 3^{-}} f(x) &= f(3), {\text{ where }} f(x) &= \sqrt{25 – x^2}\\&=\sqrt{25 -{\color{blue}3}^2 }\\&= \sqrt{16}\\&= 4\end{aligned}$ | The values from the right of $3$ lies within $1 \leq x \leq 5$. $\begin{aligned} \lim_{x \rightarrow 3^{-}} f(x) &= f(3), {\text{ where }} f(x) &= \sqrt{25 – x^2}\\&=\sqrt{25 -{\color{blue}3}^2 }\\&= \sqrt{16}\\&= 4\end{aligned}$ |
c. This means that $\boldsymbol{$\lim_{x \rightarrow 3^{-}} f(x)} = 4$.
d. The second column also shows that $\boldsymbol{$\lim_{x \rightarrow 3^{+}} f(x)} = 4$.
Comparing the results of a and b shows that the regular limit does not exist since the two limits are not equal.
$\begin{aligned} \lim_{x \rightarrow 1^{-}} f(x) &= \dfrac{1}{2}\\\lim_{x \rightarrow 1^{+}} f(x) &= 2\sqrt{6}\\\lim_{x \rightarrow 1^{-}} f(x)&\neq \lim_{x \rightarrow 1^{+}} f(x)\end{aligned}$
Comparing the results of c and d, we can show that the regular limit exists since the two limits are equal.
$\begin{aligned} \lim_{x \rightarrow 3^{-}} f(x) &= 4\\\lim_{x \rightarrow 3^{+}} f(x) &= 4\\\lim_{x \rightarrow 3^{-}} f(x)&= \lim_{x \rightarrow 3^{+}} f(x)\end{aligned}$
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
