Skew Lines – Explanation & Examples

What are skew lines? How do we identify a pair of skew lines? Let’s start with a brief definition of skew lines:

Skew lines are two or more lines that are not: intersecting, parallel, and coplanar with respect to each other.

For us to understand what skew lines are, we need to review the definitions of the following terms:

• Parallel Lines – these are lines that lie on the same plane but never meet.
• Intersecting Lines – these are lines that lie on the same plane and meet.
• Coplanar Lines – these are lines that lie on the same plane.

What if we have lines that do not meet these definitions? This is why we need to learn about skew lines.

In this article, you will learn what skew lines are, how to find skew lines, and determine whether two given lines are skewed.

What are skew lines?

Skew lines are two or more lines that do not intersect, are not parallel, and are not coplanar. (Remember that parallel lines and intersecting lines lie on the same plane.)

This makes skew lines unique – you can only find skew lines in figures with three or more dimensions.

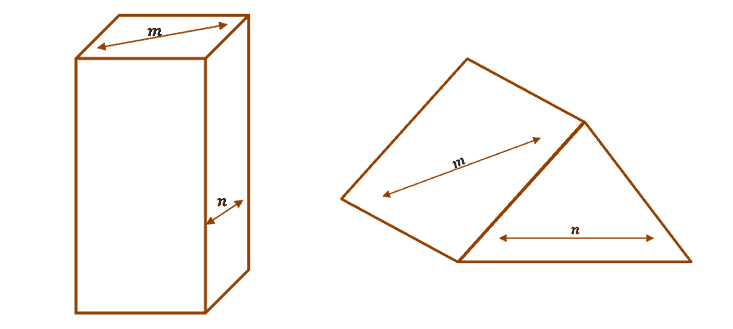
The lines $m$ and $n$ are examples of two skew lines for each figure. You can know right away by seeing how they lie on different surfaces and positioned so that they are not parallel or intersecting.

What are real-world examples of skew lines?

Since skew lines are found in three or more dimensions, our world will definitely contain skew lines. Here are some examples to help you better visualize skew lines:

• The lines found on the walls and the ceiling’s respective surfaces.
  • Since the lines on each of the surfaces are in different planes, the lines within each of the surfaces will never meet, nor will they be parallel.
• Two or more street signs lying along with the same post.
  • The lines in each street sign are not in the same plane, and they are neither intersecting nor parallel to each other.
• Roads along highways and overpasses in a city.
  • Since the roads are considered as separate planes, lines found in each will never intersect nor are parallel to each other.

How to find skew lines?

When given a figure or real-world examples, to find a pair of skew lines, always go back to the definition of skew lines. Ask the following questions:

• What are the lines (in the figure) that do not intersect each other?
• Are the chosen lines not found lying on the same plane?
• Are the chosen lines not parallel to each other?

If the answers to the three questions are YES, then you have found a pair of two lines.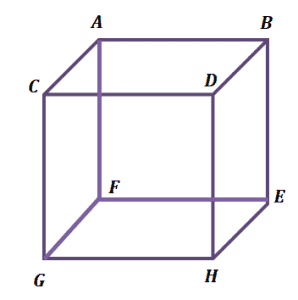

In the cube shown, $AB$ and $EH$ are examples of two lines that are skew. You can verify this by checking the conditions for skew lines.

• $AB$ and $EH$ do not intersect.
• $AB$ and $EH$ do not lie on the same plane.
• $AB$ and $EH$ are not parallel.

This confirms that the two are skew with respect to each other.

What are other skew lines’ definitions?

 We have discussed how to find skew lines from figures in the previous sections. Now, we can take a quick look into another definition of skew lines in higher mathematics.

Given two equations in vector form as shown:

$\boldsymbol{x} = \boldsymbol{x_1 }+( \boldsymbol{x_2 }- \boldsymbol{x_1})a$

$\boldsymbol{x} = \boldsymbol{x_3 }+( \boldsymbol{x_4 }- \boldsymbol{x_3})a$

They are skew lines only when $(\boldsymbol{x_1x_3})[(\boldsymbol{x_2}- \boldsymbol{x_1})(\boldsymbol{x_4}-\boldsymbol{x_3})]$ is not equal to zero.

We won’t use this definition of skew lines in a precalculus class, so for now, we can look through the equations briefly and focus on the geometrical concept of skew lines.

Example 1

1. Which of the following figures will you be able to find skew lines?
2. Hexagon
3. Cube
4. The surface of a Sphere
5. Octagon

Solution

By definition, we can only find skew lines in figures with three or more dimensions. Planes can never contain skew lines, so (a), (c), and (d) are no longer valid options.

Cubes are three-dimensional and can contain skew lines. So, it’s b.

Example 2

Which of the following examples are best represented by skew lines?

1. The length and width of a rectangular lot.
2. The two hands of a clock.
3. A southbound subway and a westbound highway.
4. The equator of the earth.

Solution

Start by eliminating options that are not skew lines:

• Which of these do not lie on the same plane? The rectangular plot (a).
• Which of these four examples do not intersect? The two hands of the clock (b).

We’re left with c and d, but the earth’s equator is just one straight line revolving around the globe. That only leaves us with c.

To confirm: a subway heading southbound and a westbound highway lie on two different roads (or planes). They will never intersect, nor are they parallel, so the two are skew lines.

Example 3

Fill in the sentences shown below with parallel, intersecting, or skew.

• The hour hand and minute hand of a clock are _______ each other.
• The vertical strings of a tennis racket are ________ to each other.
• The curtain pole along the window panes and the line along the ceiling are ______ with respect to each other.

Solution

• The two hands of the clock are connected at the center. This means that the two are intersecting each other.
• The vertical strings are lying along the same plane and direction, so they are parallel.
• The curtain pole and the line are in two different planes and will never intersect, so they are skewed with respect to each other.

Example 4

True or False? The strings along a tennis racket’s nets are considered skew to each other.

Solution

False. Since a tennis racket’s surface is considered one plane, all the strings (or the lines) found are coplanar. This means that none of them can ever be skew to each other.

Example 5

Take a screenshot or snip the image below and sketch two pairs of skew lines.

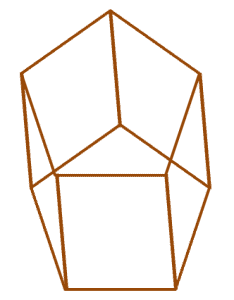
Solution

This question can have multiple possible solutions. Make use of the skew lines’ definition.  Below are three possible pairs of skew lines.

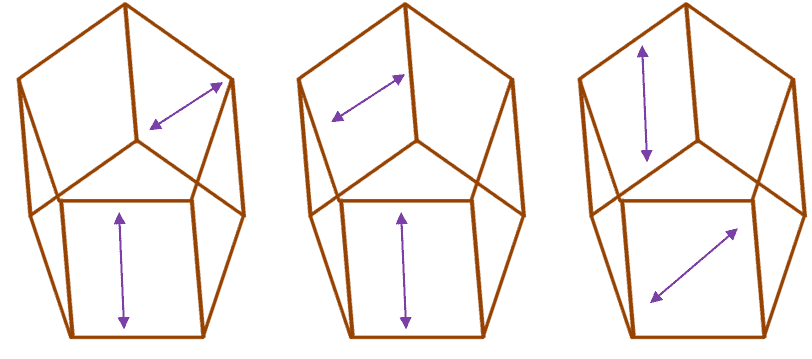
As shown in the three examples, as long as the lines are not coplanar, do not intersect, and are not parallel, they can be considered skew lines.

Example 6

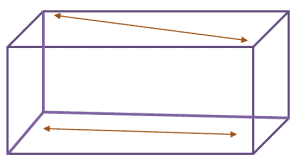
Take a screenshot or snip the image below and sketch one line that will still be skew with the two other lines.

Solution

Look for a third segment in the figure above that does not lie on the same planes as the two given lines.

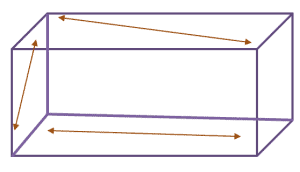
This problem has multiple possible answers. As long as the third line remains skewed with the two given lines, the answer is valid.

Example 7

Aside from AB and EH, name two other pairs of skew lines in the cube shown.

Solution

Look for two segments in the cube that do not lie on the same plane and do not intersect.

Other examples of skew lines are: $AC$ and $DH$, $AF$ and $GH$, and $BE$ and $CG$.

There can be more variations as long as the lines meet the definition of skew lines.

Example 8

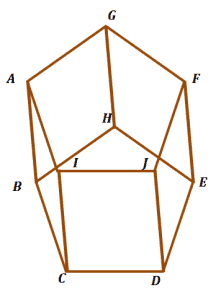
Identify three pairs of skew lines in the figure shown below.

Solution

Look for three pairs of segments in the figure above that do not lie on the same plane, are not parallel, and do not intersect.

Three possible pairs of skew lines are: $AI$ and $DE$, $FE$ and $IC$, as well as $BC$ and $GF$.

This problem has multiple possible answers. As long as the lines meet the definition of skew lines, the three pairs will be valid.