Limits of rational functions – Examples and Explanation

What happens when a ration function approaches infinity? How do we estimate the limit of a rational function? We will answer these questions as we learn about the limits of rational functions.

The limits of rational functions tell us the values that a function approaches at different input values.

Need a refresher on rational functions? Check out this article we wrote to help you review. In this article, we’ll learn about the different techniques in finding the limits of rational functions.

A rational function’s limits can help us predict the behavior of the function’s graph at the asymptotes. These values can also tell us how the graph approaches the coordinate system’s negative and positive sides.

How to find the limit of a rational function?

Finding the limit of rational functions can be straightforward or require us to pull up some tricks. In this section, we’ll learn the different approaches we can use to find the limit of a given rational function.

Recall that rational functions are ratios of two polynomial functions. For example, $f(x) = \dfrac{p(x)}{q(x)}$, where $q(x) \neq 0$.

Limits of rational functions can either be of the form: $\lim_{x\rightarrow a} f(x)$ or $\lim_{x\rightarrow \pm \infty} f(x)$.

As a refresher, this is how we interpret the two:

Why don’t we start by learning how we can calculate a rational function’s limits as it approaches a given value?

Finding the limit as $\boldsymbol{x\rightarrow a}$

When we find the limit of $f(x)$ as it approaches $a$, there can be two possibilities: the functions have no restrictions at $x = a$ or it has.

• When $a$ is part of $f(x)$’s domain, we substitute the values into the expression to find its limit.
• When $a$ is not part of $f(x)$’s domain, we try to eliminate the factor corresponding to it then find the value of $f(x)$ using its simplified form.
• Does the function contain a radical expression? Try multiplying both numerator and denominator by the conjugate.

Let’s try observing $f(x) = \dfrac{x – 1}{(x – 1)(x + 1)}$ as it approaches $3$. To better understand what limits represent, we can construct table of values for $x$ close to $3$.

Do you have a guess on what the values of $\lim_{x\rightarrow 3} \dfrac{x – 1}{(x – 1)(x + 1)}$ is? Since $3$ is part of the domain of $f(x)$ (restricted values for $x$ are $1$ and $-1$), we can substitute $x = 3$ into the equation right away.

$\begin{aligned} \lim_{x\rightarrow 3} \dfrac{x – 1}{(x – 1)(x + 1)} &= \dfrac{3 – 1}{(3 – 1)(3 + 1)}\\&=\dfrac{2}{2 \cdot 4}\\&=\dfrac{1}{4}\\&=0.25\end{aligned}$

As you might have guessed, as $x$ approaches $3$, $f(x)$ is equal to $0.25$.

Now, what if we want to find $\lim_{x\rightarrow 1} \dfrac{x – 1}{(x – 1)(x + 1)}$? Since $x = 1$ is a restriction, we can try to simplify $f(x)$ first to remove $x – 1$ as a factor.

$\begin{aligned} \lim_{x\rightarrow 1} \dfrac{x – 1}{(x – 1)(x + 1)} &= \lim_{x\rightarrow 1} \dfrac{\cancel{(x – 1)}}{\cancel{(x – 1)}(x + 1)}\\&=\lim_{x\rightarrow 1} \dfrac{1}{x + 1}\end{aligned}$

Once we have removed the common factors, we can apply the same process and substitute $x = 1$ into the simplified expression.

$\begin{aligned} \lim_{x\rightarrow 1} \dfrac{1}{x + 1}&=\dfrac{1}{1 + 1}\\&=\dfrac{1}{2}\end{aligned}$

Ready to try more problems? Don’t worry. We have prepared a lot of examples for you to work on. For now, let’s learn about limits at infinity.

Finding the limit as $\boldsymbol{x\rightarrow \infty}$

There are instances when we need to know how a rational function behaves on both sides (positive and negative sides). Knowing how to find the limits of $f(x)$ as it approaches $\pm \infty$ can help us predict this.

The value of $\lim_{x\rightarrow \pm \infty } f(x)$ can be determined based on its degrees. Let’s say we have $f(x) = \dfrac{p(x)}{q(x)}$ and $m$ and $n$ are the degrees of the numerator and denominator, respectively.

The table below summarizes the behavior of $f(x)$ as it approaches $\pm infty$.

Let’s observe the graphs of three rational functions reflecting the three cases we’ve discussed.

• When the degree of the numerator is smaller such as $f(x) = \dfrac{2}{x}$.
• When the degree of the numerator is smaller such as $f(x) = \dfrac{x^2 – 1}{x – 2}$.
• When the degree of the numerator and denominators are equal such as $f(x) = \dfrac{5x^2 – 1}{x^2 + 3}$.

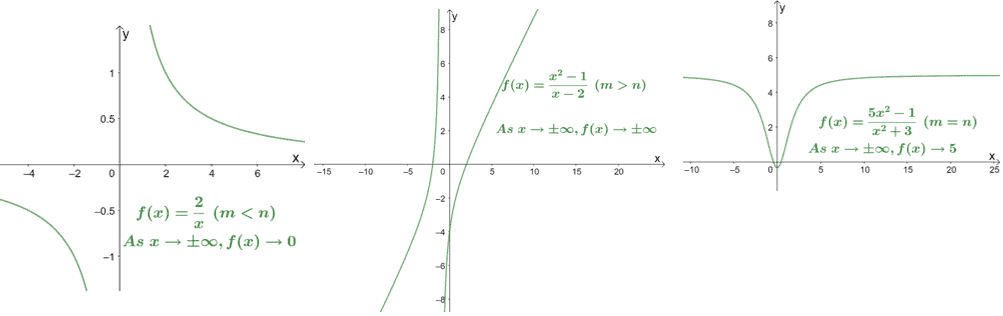
Their graphs also confirm the limits we’ve just evaluated. Knowing the limits ahead of time can also help us predict how the graphs behave.

These are the techniques we need at this point – don’t worry, you’ll learn more about limits in your Calculus class. For now, let’s go ahead and practice finding the limits of different rational functions.

Example 1

Evaluate the following limits shown below.

  a. $\lim_{x\rightarrow 4} \dfrac{x – 1}{x + 5}$
    b. $\lim_{x\rightarrow -2} \dfrac{x^2 – 4}{x^3 + 1}$
    c. $\lim_{x\rightarrow 3} \dfrac{4x^3 + 2x – 1}{x^2 + 2}$
Solution
Let’s start with the first function, and since $x = 4$ is not a restriction of the function, we can substitute the $x = 4$ into the expression right away.
$ \begin{aligned} \lim_{x\rightarrow 4} \dfrac{x – 1}{x + 5}&=\dfrac{4 – 1}{4 + 5}\\&=\dfrac{3}{9}\\&=\dfrac{1}{3}\end{aligned}$
a. Hence, we have $\lim_{x\rightarrow 4} \dfrac{x – 1}{x + 5} = \boldsymbol{\dfrac{1}{3}}$.
We apply the same process for b and c since $\dfrac{x^2 – 4}{x^3 + 1}$ and $\dfrac{4x^3 + 2x – 1}{x^2 + 2}$ has no restrictions at $x = -2$ and $x = 3$, respectively.
$\begin{aligned} \lim_{x\rightarrow -2} \dfrac{x^2 – 4}{x^3 + 1}&=\dfrac{(-2)^2 – 4}{(-2)^3 + 1}\\&=\dfrac{4 – 4}{-8 + 1}\\&=\dfrac{0}{-7}\\&= 0\end{aligned}$
b. This means that $\lim_{x\rightarrow -2} \dfrac{x^2 – 4}{x^3 + 1} = \boldsymbol{0}$.
$\begin{aligned} \lim_{x\rightarrow 3} \dfrac{4x^3 + 2x – 1}{x^2 + 2}&=\dfrac{4(3)^3 + 2(3) -1}{(3)^2 + 2}\\&=\dfrac{108 +6 – 1}{9 + 2}\\&=\dfrac{101}{11}\end{aligned}$
c. Hence, $\lim_{x\rightarrow 3} \dfrac{4x^3 + 2x – 1}{x^2 + 2} = \boldsymbol{\dfrac{101}{11}}$.

Example 2

What is the limit of $f(x) = \dfrac{2x – 4}{3x^2 – 12}$ as it approaches $2$?

Solution

We can check if $f(x)$ has restrictions on $x = 2$, we can find the value of $3x^2 – 12$ when $x = 2$: $3(2)^2 – 12 = 0$.

This means that we can’t just substitute $x$ back into $f(x)$ right away. Instead, we can express $f(x)$’s numerator and denominator in factored forms first.

$\begin{aligned} f(x)&= \dfrac{2x – 4}{3x^2 – 12}\\&= \dfrac{2(x – 2)}{3(x^2 – 12)}\\&= \dfrac{2(x – 2)}{3(x – 2)(x + 2)}\end{aligned}$

Cancel the common factors first to remove the restriction on $x = 2$. We can then find the limit of $f(x)$ as it approaches $2$.

$ \begin{aligned} f(x)&=  \dfrac{2\cancel{(x – 2)}}{3\cancel{(x – 2)}(x + 2)}\\&=\dfrac{2}{3(x + 2)}\\\\\lim_{x\rightarrow 4} f(x)&=\lim_{x\rightarrow 2} \dfrac{2}{3(x + 2)}\\&=\dfrac{2}{3(4 + 2)}\\&=\dfrac{2}{3(6)}\\&=\dfrac{1}{9}\end{aligned}$

This means that $\lim_{x\rightarrow 4} f(x) = \boldsymbol{ \dfrac{1}{9}}$.

Example 3

If $\lim_{x\rightarrow \infty} f(x) = 0$, which of the following statements is true?

    a. The ratio of the $f(x)$’s leading coefficients is equal to one.

    b. The degree of the numerator is greater than the degree of the denominator of $f(x)$.

    c. The degree of the numerator is less than the degree of the denominator of $f(x)$.

    d. The degree of the numerator is equal to the degree of the denominator of $f(x)$.

Solution

The limit of a rational function as it approaches infinity will have three possible results depending on $m$ and $n$, the degree of $f(x)$’s numerator and denominator, respectively:

Since we have $\lim_{x\rightarrow \infty} f(x) = 0$, the degree of the function’s numerator is less than that of the denominator.

Example 4

Using the graph shown below, what is the ratio of the leading coefficients of $f(x)$’s numerator and denominator?

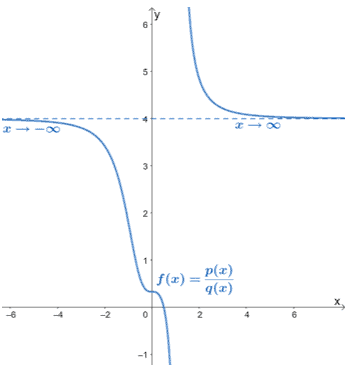
Solution

From this graph, we can see that $\lim_{x\rightarrow \infty} f(x) = 4$. Since the limit is not zero or infinity, the limit for $f(x)$ reflects the ratio of the leading coefficients of $p(x)$ and $q(x)$.

This means that the ratio is equal to $\boldsymbol{4}$.

Example 5

What is the limit of $f(x) = \dfrac{x}{\sqrt{x+16} – 4}$ as $x$ approaches $0$?

Solution

Let’s check $f(x)$ for restrictions at $x =4$ by seeing the value of the denominator when $x = 0$.

$ \begin{aligned}\sqrt{0+16}- 4 &= 4 –  4\\&= 0\end{aligned}$

This means that we need to manipulate $f(x)$ by multiplying both its numerator and denominator by the conjugate of $\sqrt{x+16} – 4$.

$\begin{aligned}f(x)&= \dfrac{x}{\sqrt{x + 16} – 4}\cdot \dfrac{\sqrt{x+16} + 4}{\sqrt{x+16} + 4}\\&= \dfrac{x(\sqrt{x+16} + 4)}{(\sqrt{x+16} – 4)(\sqrt{x+16} + 4)}\\&= \dfrac{x(\sqrt{x+16} + 4)}{(\sqrt{x+16})^2 – (4)^2}\\&= \dfrac{x(\sqrt{x+16} + 4)}{x+16 – 16}\\&= \dfrac{\cancel{x}(\sqrt{x+16} + 4)}{\cancel{x}}\\&=\sqrt{x+16}+4\end{aligned}$

Make sure to review how we rationalize radicals using conjugates by checking out this article.

Now that $f(x)$ has been rationalized, we can now find the limit of $f(x)$ as $x \rightarrow 0$.

$\begin{aligned}\lim_{x\rightarrow 0} f(x)&=\lim_{x\rightarrow 0} \sqrt{x + 16} – 4\\&=\sqrt{0 + 16} – 4\\ &= 4 – 4\\&= 0\end{aligned}$

Hence, the limit of $f(x)$ as it approaches $0$ is equal to $\boldsymbol{0}$.