- Home
- >
- Hyperbola – Properties, Components, and Graph
Hyperbola – Properties, Components, and Graph
 The hyperbola is a unique type of conic section where we see two disjointed curves representing its equation. These conics are used in describing the pathways of a spacecraft and are even used to model certain seismological events.
The hyperbola is a unique type of conic section where we see two disjointed curves representing its equation. These conics are used in describing the pathways of a spacecraft and are even used to model certain seismological events.
Hyperbolas are conic sections that are the result of a plane intersecting both surfaces of a double cone. Their graphs are like two U-shaped curves that are facing each other vertically or horizontally.
You may have been introduced to hyperbolas when you first learned about conic sections, so if you need a quick refresher, feel free to take a look at this article to see what makes hyperbolas different from parabolas and ellipses.
In this article, we’ll focus on hyperbolas and learn the following:
- Understanding how hyperbolas are obtained and the different components it contains.
- Identify the different standard forms of a hyperbola equation.
- Know how to represent these conics on the $xy$-coordinate system.
We’ll also try out doing the reverse- finding the equations representing the hyperbolas given their graphs. This article thoroughly covers all components of hyperbolas, so make sure to take notes.
For now, why don’t we begin by refreshing how hyperbolas are formed using a double cone and a plane?
What is a hyperbola?
Hyperbolas result when a plane and right double cone intersect each other and cover upper and lower intersections, as shown below.
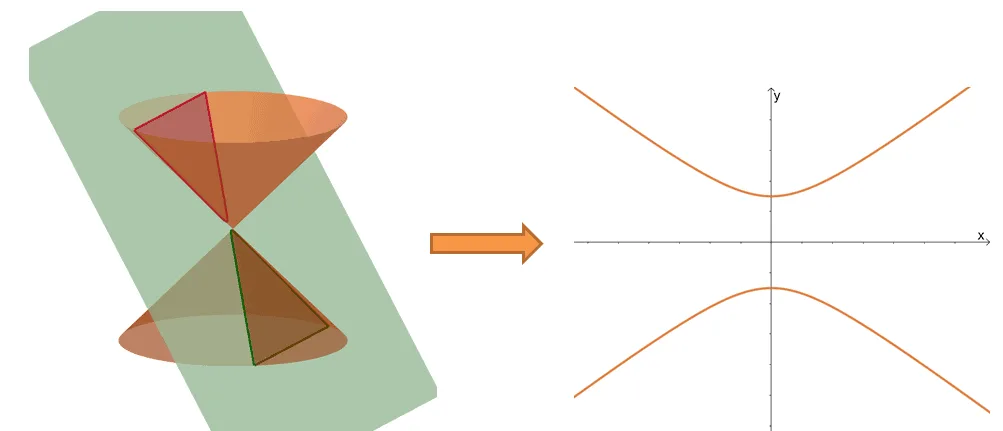
This means that hyperbolas are two U-shaped curves (called branches) that face opposite each other. They can either be oriented vertically as our example or oriented horizontally.
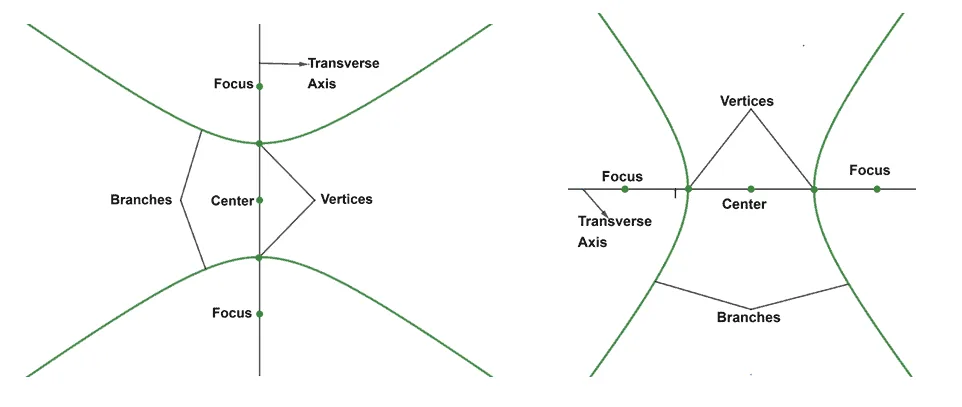
The image above shows us the different components of a hyperbola regardless of their orientation.
- Hyperbolas have two curves called the branches facing opposite each other.
- Since they have two U-shaped curves, hyperbolas will also have two vertices and foci.
- The transverse axis is a guiding axis that divides the hyperbola in half.
Formal hyperbola definition
The components mentioned above help us define hyperbolas formally. Hyperbolas are conic sections where all points that lie on their graphs satisfy the following condition:
- Let’s say $P(x,y)$ lies on the hyperbola, determine the distances between $P$ and the two foci.
- When lying on a hyperbola, the difference between these two distances will always be constant.
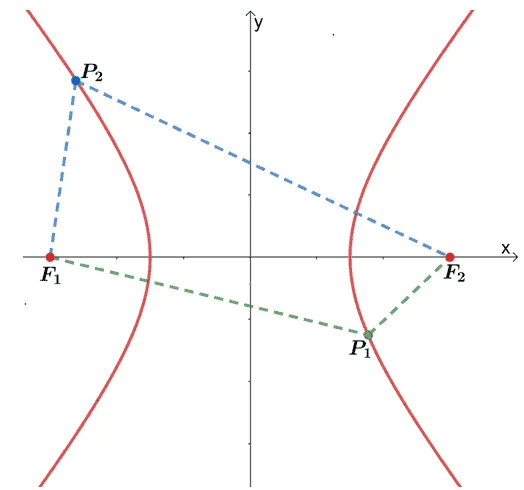
This means that for hyperbolas like the image shown above, $P_1$ and $P_2$ are two points lying on the hyperbola. The (absolute value) difference between $\overline{P_2F_1}$ and $\overline{P_2F_2}$ will be equal to the difference between $\overline{P_1F_1}$ and $\overline{P_1F_2}$.
All hyperbolas’ variations will satisfy these conditions, and these conditions make hyperbolas unique from the rest of the conic sections.
How to find the equation of a hyperbola?
Four standard forms are important for us to keep in mind when working with hyperbolas and their equations. The factors affecting the form of the hyperbola’s equation are the following:
- The center of a hyperbola will affect its equation.
- The orientation of the graph will affect which term would be placed first.
Hyperbola formula in standard forms
We’ll divide this section into the standard forms of the hyperbola centered at the origin, $(0, 0)$, and centered at the vertex, $(h, k)$.
Standard Form of Hyperbolas Centered at the Origin
When hyperbolas are centered at the origin, we expect no constants inside the squared term. Here’s a table showing the two possible forms of the equation:
Parabola’s Orientation | Equation |
Vertical | $\dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1$ |
Horizontal | $\dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1$ |
We can see that the leading term gives us an idea of how the hyperbola’s graph will appear – when the leading term is $x^2$, the hyperbolas are symmetric horizontally. Similarly, when $y^2$ is the leading term, the hyperbolas will be symmetric vertically.
Standard Form of Hyperbolas Centered at $\boldsymbol{(h, k)}$
When hyperbolas are not centered at the origin and instead at $(h, k)$.
Parabola’s Orientation | Equation |
Vertical | $\dfrac{(y – k)^2}{a^2} – \dfrac{(x – h)^2}{b^2} = 1$ |
Horizontal | $\dfrac{(x –h)^2}{a^2} – \dfrac{(y –k)^2}{b^2} = 1$ |
The only difference between these pair of equations is the fact that the hyperbola is translated $h$ units horizontally and $k$ units vertically. The rest of the hyperbola’s components will also be affected by this translation.
How to find the vertices of a hyperbola?
The vertices of a hyperbola are the two points showing the minimum and maximum values possible for the leading term. Regardless of the center’s location, the vertices’ distance from the center will be dependent on the first denominator.
| Equation | Center | Vertex |
| $\dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1$ | $(0,0)$ | $(0, -a), (0, a)$ |
| $\dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1$ | $(-a, 0), (a, 0)$ | |
| $\dfrac{(y – k)^2}{a^2} – \dfrac{(x – h)^2}{b^2} = 1$ | $(h, k)$ | $(h, k-a), (h, k + a)$ |
| $\dfrac{(x –h)^2}{a^2} – \dfrac{(y –k)^2}{b^2} = 1$ | $(h -a , k), (h + a, k)$ |
To summarize the table shown above, to find the vertices, we can either:
- Move $a$ units to both directions of the center when we need the graph of the hyperbola.
- Add and subtract $a$ from the center’s coordinate – whichever is the leading term, that’s the coordinate we’ll be adding and subtracting $a$ from.
How to find the foci of a hyperbola?
The foci will depend on the values of the denominators from the hyperbola’s equation.
\begin{aligned}c^2 = a^2 + b^2\end{aligned}
This means that we can find the distance of the foci from the center by adding the denominators and then taking the sum’s square root.
Once we have the value of $c$, we move $c$ units away from the center to locate the hyperbola’s two foci.
| Equation | Center | Vertex |
| $\dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1$ | $(0,0)$ | $(0, -c), (0, c)$ |
| $\dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1$ | $(-c, 0), (c, 0)$ | |
| $\dfrac{(y – k)^2}{a^2} – \dfrac{(x – h)^2}{b^2} = 1$ | $(h, k)$ | $(h, k-c), (h, k + c)$ |
| $\dfrac{(x –h)^2}{a^2} – \dfrac{(y –k)^2}{b^2} = 1$ | $(h -c , k), (h + c, k)$ |
This means that we count $c$ units on both sides of the center and along the direction of the hyperbola to find the foci from the center.
How to find the asymptotes of a hyperbola?
Hyperbolas have a pair of asymptotes that have a general form of $y = mx + b$. This means that we’re looking for two linear equations when finding the asymptotes of a hyperbola.
The asymptotes’ equations will depend on the square roots of the denominators. We can also find the hyperbola equation centered at $(h, k)$ by simply translating it.
Equation | Asymptotes’ Equations | |
| $\dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1$ | $y = \dfrac{a}{b}x$ | $y = -\dfrac{a}{b}x$ |
| $\dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1$ | $y = \dfrac{b}{a}x$ | $y = -\dfrac{b}{a}x$ |
| $\dfrac{(y – k)^2}{a^2} – \dfrac{(x – h)^2}{b^2} = 1$ | $y – k = \dfrac{a}{b}(x – h)$ | $y – k= -\dfrac{a}{b}(x – h)$ |
| $\dfrac{(x –h)^2}{a^2} – \dfrac{(y –k)^2}{b^2} = 1$ | $y – k = \dfrac{b}{a}(x – h)$ | $y – k= -\dfrac{b}{a}(x – h)$ |
This table summarizes the standard forms of the asymptotes. From this, we can see that:
- When the leading term has $y^2$ on the numerator, the numerator of the asymptote’s constant will be $a$.
- When the leading term has $x^2$ on the numerator, the numerator of the asymptote’s constant will be $b$.
- The asymptotes of the hyperbolas centered at $(h, k)$ will have equations that will have similar forms except that we have $(y – k)$ and $(x – h)$ to account for the translation.
Just make sure to note the leading terms and the coefficients’ order as the common mistakes may occur here.
When given the hyperbola graph and we need to determine its equation, knowing the form of the asymptotes will be helpful. We can use the value of $a$ and eventually solve for $b$. Don’t worry, the last problem in the next section will show you exactly what we mean.
How to graph a hyperbola?
Now that we understand the general forms of hyperbolas and learn how to find their components, it’s time that we learn how to graph hyperbolas as well.
Here are four graphs, and it’s best to familiarize yourself with these as they are the four main types of graphs we’ll encounter in the examples below.
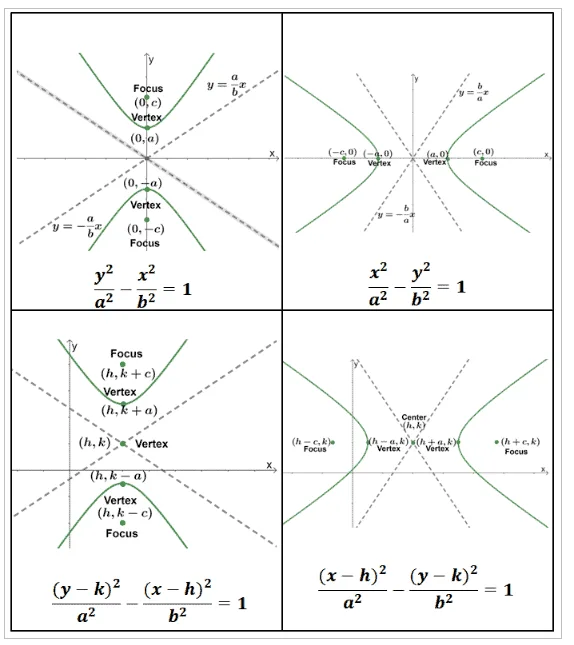
From these graphs, we can confirm what we’ve learned about hyperbolas and their components:
- When the leading term is $x^2$, the parabola’s are oriented horizontally, meaning the branches open to the left and right.
- Meanwhile, when the leading term is $y^2$, the parabolas are oriented vertically, meaning the branches open upward and downward.
- The foci and vertices can be determined by finding the points that are $c$ and $a$ units away from the center but along the direction of the parabola.
Here are six steps to help guide you in graphing a hyperbola.
| Step 1: | Locate and plot the center of the hyperbola. |
| Step 2: | Locate and plot the vertices and foci of the hyperbola. |
| Step 3: | If possible, plot its intercepts as well for additional guide points. |
| Step 4: | Find the asymptotes and present them as dashed lines. |
| Step 5: | Locate and plot the vertices and foci of the hyperbola. |
| Step 6: | Graph the two branches of the hyperbola using the vertices and asymptotes as a guide. |
You can also create a guide rectangle using the values of the denominator – construct a dashed rectangle with vertices, $(a, b)$, $(-a,b)$, $(a, -b)$, and $(-a,-b)$ for hyperbolas that open to the sides. Use $(b, a)$, $(-b, a)$, $(b, -a)$, and $(-b, -a)$ when they open upwards and down wards.
The asymptotes will pass through the vertices, so it’ll make Step 4 easier as well.
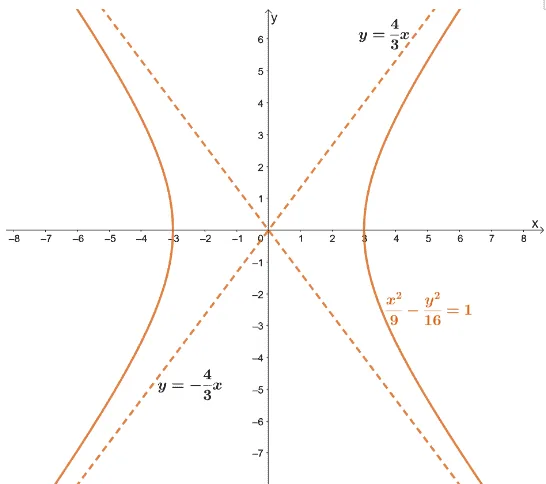
Why don’t we review these steps and tips by graphing the hyperbola represented by the equation, $\dfrac{x^2}{9} – \dfrac{y^2}{16} = 1$?
Step 1: The center of this hyperbola will be at the origin – $(0, 0)$.
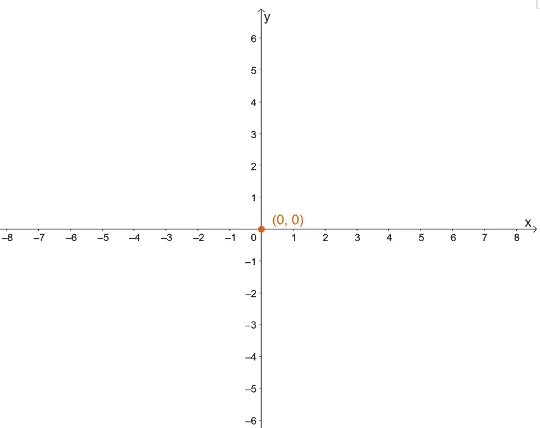
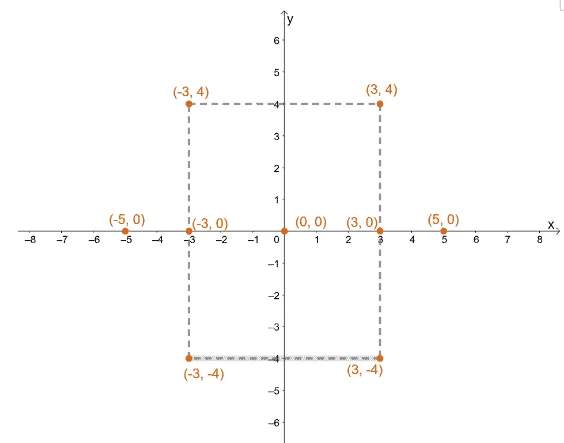
Step 2 – 3: Since the leading term is $\dfrac{x^2}{9}$, we can see that the vertices will be at $(-3, 0)$ and $(3, 0)$.
- Find the distance of the foci from the center using $c^2 = a^2 + b^2$. We can ss that $c^2 = 25$ and consequently, the foci of the hyperbola are $(-5, 0)$ and $(5, 0)$.
- Let’s include the points of the vertices of the imaginary rectangular to guide us: $(3, 4)$, $(-3, 4)$, $(3, -4)$, and $(-3, -4)$.
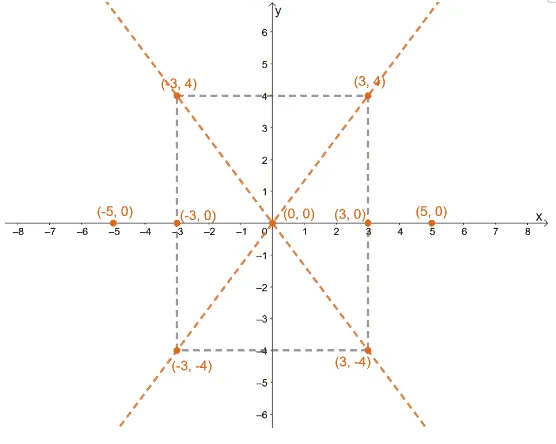
Step 4: The standard forms of the asymptotes for the hyperbola are $y = \pm \dfrac{b}{a}x$. Hence, we have $y = \dfrac{4}{3}x$ and $y = -\dfrac{4}{3}x$.
Step 5: Graph the curves of the hyperbola using the vertices and the asymptotes as a guide.
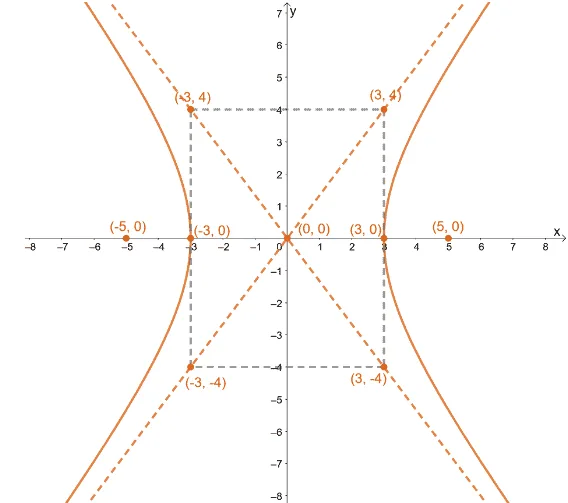
This shows how the hyperbola and the important components can help us understand how to graph the hyperbola. We can take off the guide points to finalize the graph of the hyperbola, as shown below.
Make sure to review the important sections we’ve discussed and note how each component relates to the other. When you’re ready, we have more questions (with complete explanation) prepared to help you master this topic.
Example 1
Use your knowledge about hyperbolas and fill in the blanks to make the following statements true.
a. The vertices of $\dfrac{x^2}{16} – \dfrac{y^2}{9} = 1$ are ________ and __________.
b. The foci of $\dfrac{x^2}{36} – \dfrac{y^2}{64} = 1$ are located at ________ and __________.
c. The asymptotes for the hyperbola, $\dfrac{y^2}{25} – \dfrac{x^2}{36} = 1$, have equations of _____________ and _____________.
Solution
The vertices will depend on the leading term of the hyperbola’s equation, $\dfrac{x^2}{16} – \dfrac{y^2}{9} = 1$. This means that $a^2 = 16$ and so, $a = 4$.
Since the center of the hyperbola is $(0, 0)$ and the branches are opening to the right and left so that the vertices will be $(-a, 0)$ and $(a, 0)$.
a. The hyperbola’s vertices will be $(-4, 0)$ and $(4, 0)$.
Now, to find the foci of $\dfrac{x^2}{36} – \dfrac{y^2}{64} = 1$, we add the denominators then take the square root of the result.
\begin{aligned}c^2 &= 36 + 64\\&= 100\\c&= 10\end{aligned}
The hyperbola is still centered at the origin, and the branches will be opening to the left and to the right so that the foci will be of the forms $(-c, 0)$ and $(c, 0)$.
b. This means that the hyperbola’s foci are $(-10,0)$ and $(10, 0)$.
Since the leading term of the hyperbola’s equation is $y^2$ and the hyperbola’s center is $(0, 0)$, the asymptotes will be of the forms, $y = \pm \dfrac{a}{b}x$.
$\boldsymbol{a}$ | $\boldsymbol{b}$ | $\boldsymbol{y = \pm \dfrac{a}{b} x}$ |
\begin{aligned}a^2 &= 36\\a&= 6\end{aligned} | \begin{aligned}b^2 &= 64\\b&= 8\end{aligned} | \begin{aligned}y&= \dfrac{3}{4}x \\ y&= – \dfrac{3}{4}x\end{aligned} |
c. Hence, the equations of the asymptotes are $y = \dfrac{3}{4}x$ and $y = -\dfrac{3}{4}x$.
Example 2
Identify the center, vertices, and foci of the following hyperbolas.
a. $\dfrac{x^2}{49} – \dfrac{y^2}{32} = 1$
b. $\dfrac{y^2}{144} – \dfrac{x^2}{81} = 1$
c. $\dfrac{(x – 2)^2}{25} – \dfrac{(y + 4)^2}{11} = 1$
d. $\dfrac{(y + 1)^2}{64} – \dfrac{(x – 5)^2}{36} = 1$
Solution
We can divide the problem into pairs of items – depending on the centers that these problems have.
- For the first two equations, since the numerators are solely $x^2$ and $y^2$ without any additional constants, we expect their centers to be at the origin.
- The vertices will depend on the leading terms’ denominators, so we take the square root of $49$ and $144$.
- The foci’s distance from the center can be calculated using $c^2 = a^2 + b^2$, where $c$ represents the foci’ distance from the center.
- When $x^2$ is the leading term, these components will be reflected on the $x$-coordinates, while the second equation will have these values on the $y$-component.
Equation | Center | Vertices | Foci |
\begin{aligned}\dfrac{x^2}{49} – \dfrac{y^2}{32} &= 1\end{aligned} | \begin{aligned}(0,0) \end{aligned} | \begin{aligned} a^2 &= 49\\a&= 7\\\\\text{vertices: }&= (-7, 0), (7, 0)\end{aligned} | \begin{aligned} c^2 &= 49 + 32\\ &= 81\\c&= 9\\\\\text{foci: }&= (-9, 0), (9, 0)\end{aligned} |
\begin{aligned}\dfrac{y^2}{144} – \dfrac{x^2}{81} &= 1\end{aligned} | \begin{aligned}(0,0) \end{aligned} | \begin{aligned} a^2 &= 144\\a&= 12\\\\\text{vertices: }&= (0, -12), (0, 12)\end{aligned} | \begin{aligned} c^2 &= 144 + 81\\ &= 225\\c&= 15\\\\\text{foci: }&=(-15, 0), (15, 0)\end{aligned} |
Let’s work on the two remaining equations and begin by finding the centers found at $(h, k)$.
- For the third equation, the vertices and the foci can be determined by counting $a$ and $c$ units to the left and the center’s right.
- On the other hand, the fourth equation will have vertices, and the foci located $a$ and $c$ units above and below the center.
Equation | Center | Vertices | Foci |
\begin{aligned}\dfrac{(x – 2)^2}{25} – \dfrac{(y + 4)^2}{11} &= 1\end{aligned} | \begin{aligned}(2,-4) \end{aligned} | \begin{aligned} a^2 &= 25\\a&= 5\\\\\text{vertices: }&=(-3, -4), (7, -4)\end{aligned} | \begin{aligned} c^2 &= 25 + 11\\ &= 36\\c&= 6\\\\\text{foci: }&=(-4, -4), (8, -4)\end{aligned} |
\begin{aligned}\dfrac{(y + 1)^2}{64} – \dfrac{(x – 5)^2}{36} &= 1\end{aligned} | \begin{aligned}(5,-1) \end{aligned} | \begin{aligned} a^2 &= 64\\a&= 8\\\\\text{vertices: } &= (5, -9), (5, 7)\end{aligned} | \begin{aligned} c^2 &= 64 + 36\\ &= 100\\c&= 10\\\\\text{foci: }&=(5, -11), (5, 11)\end{aligned} |
This example shows how it’s possible for us to identify different components of hyperbolas using their equations. Now, what if we’re given these components and we need to find the equation instead?
Example 3
Use the given components of the hyperbolas to find the equations that represent these hyperbolas.
a. A hyperbola with a foci of $(-4, 0)$ and $(4, 0)$ and vertices at $(-3, 0)$ and $(3, 0)$.
b. A hyperbola with a foci of $(0, -9)$ and $(0, 9)$ and vertices at $(0,-4)$ and $(0, 4)$.
c. A hyperbola with a center at $(-4, 5)$, a focus at $(-8, 5)$, and a vertex at $(-6, 5)$.
d. A hyperbola with a center at $(-6, -8)$, a focus at $(-6, -3)$, and a vertex at $(-6, -5)$.
Solution
For the first hyperbola, we can see that both pairs of foci and vertices lie along the $x$-axis. This means that the hyperbola’s branches are opening to the left and to the right.
- From this, we can see that the standard form of the equation is $\dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1$.
- Since the vertices are $(-3, 0)$ and $(3, 0)$, we have $a = 3$.
- From the foci, we have $c = 4$ and consequently $c^2 = 16$.
We can calculate $b^2$ using the fact that $c^2 = a^2 + b^2$.
\begin{aligned}c^2 &= a^2 + b^2 \\16&= 3^2 + b^2\\b^2&= 7\end{aligned}
Now that we have $a^2$ and $b^2$, we can now write the equation representing the first hyperbola.
a. The hyperbola’s equation is $\dfrac{x^2}{9} – \dfrac{y^2}{7} = 1$.
We can apply a similar approach to the second item, but this time, the leading term will be $y^2$ since the foci and vertices are located along the $y$-axis.
- This means that the standard form of the equation is $\dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1$.
- Since the vertices are $(0, -4)$ and $(0, 4)$, we have $a = 4$.
- From the foci, we have $c = 9$ and consequently $c^2 = 81$.
We can also calculate $b^2$ the same way we did with the previous hyperbola. Hence, we have the following.
\begin{aligned}c^2 &= a^2 + b^2 \\81&= 4^2 + b^2\\b^2&= 65\end{aligned}
We can now find the equation of the hyperbola for the second item using the values of $a^2$ and $b^2$.
b. The hyperbola’s equation is $\dfrac{y^2}{4} – \dfrac{x^2}{65} = 1$.
The third hyperbola’s center is given, so we’re expecting the equation to contain $(x –h)^2$ and $(y – k)^2$ in the numerators.
- Since only the $x$-coordinates are changing for the vertices and foci, the hyperbola’s branches open to the left and to the right.
- The distance of the given vertex from the center is $2$, so $a = 2$ and $a^2 = 4$.
- Similarly, since the distance of the given focus and the center is $4$, $c = 4$ and $c^2 =16$.
The graph’s standard form will be $\dfrac{(x –h)^2}{a^2} – \dfrac{(y – k)^2}{b^2} = 1$, so we still need to find value of $b^2$. We can do so using the formula, $c^2 = a^2 + b^2$.
\begin{aligned}c^2 &= a^2 + b^2 \\16&= 4^2 + b^2\\b^2&= 12\end{aligned}
c. Using $(h, k)= (-4, 5)$, $a^2 = 4^2$, and $b^2 = 12$, the equation of the third hyperbola is $\dfrac{(x + 4)^2}{16} – \dfrac{(y – 5)^2}{12} = 1$.
We’ll apply a similar process to find the equation of the fourth hyperbola.
- Since only the $y$-coordinates are changing for the vertices and foci, the hyperbola’s branches to open upward and downward with a standard form of $\dfrac{(y –k)^2}{a^2} – \dfrac{(x – h)^2}{b^2} = 1$.
- The distance of the given vertex from the center is $3$, so $a = 3$ and $a^2 = 9$.
- Similarly, since the distance of the given focus and the center is $5$, $c = 5$ and $c^2 =25$.
Let’s use these information and the formula, $c^2 = a^2 + b^2$ to find $b^2$.
\begin{aligned}c^2 &= a^2 + b^2 \\25&= 9 + b^2\\b^2&= 16\end{aligned}
d. Using $(h, k)= (-6, -8)$, $a^2 = 9$, and $b^2 = 16$, the equation of the third hyperbola is $\dfrac{(y + 8)^2}{9} – \dfrac{(x + 6)^2}{16} = 1$.
Example 4
Graph the hyperbola represented by the following equations. Make sure to include the foci, vertices, and asymptotes of the hyperbola as well.
a. $\dfrac{y^2}{25} – \dfrac{x^2}{64} = 1$
b. $8x^2 – 50y^2 = 200$
Solution
Let’s inspect the first equation and we can see that its standard form is $\dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1$.
- This means that the hyperbola’s center is $(0, 0)$.
- Since the leading term has $y^2$ at its numerator, the hyperbola’s branches are opening upward and downward.
- This also means that the vertices will be positioned at $(0, -a)$, $(0, a)$, $(0, -b)$, and $(0, b)$.
- The hyperbola’s asymptotes are also of the form $y = \pm \dfrac{a}{b} x$.
$\boldsymbol{a}$ | $\boldsymbol{b}$ | Vertices | Asymptotes |
\begin{aligned}a^2 &= 25\\ a&= 5\end{aligned} | \begin{aligned}b^2 &= 64\\ b&= 8\end{aligned} | \begin{aligned}(0,-5), (0, 5)\end{aligned} | \begin{aligned} y &= \pm \dfrac{a}{b} x \\ y&= \dfrac{5}{8} x\\y&= -\dfrac{5}{8}x\end{aligned} |
To find the foci’s coordinates, let’s go ahead and use the formula, $c^2 = a^2 + b^2$, where $c$ represents the distance of the foci from the center .
\begin{aligned}c^2 &= 25 + 64 \\&= 89\\c&= sqrt{89}\\&\approx 9.43\\\\\text{foci: } &= (0, -\sqrt{89}), (0, \sqrt{89})\end{aligned}
We can begin by plotting the vertices, foci, and asymptotes. The hyperbola’s asymptotes can be graphed faster if we add a rectangle as guide with corners at $(8, 5)$, $(-8, 5)$, $(8, -5)$, and $(-8, -5)$.
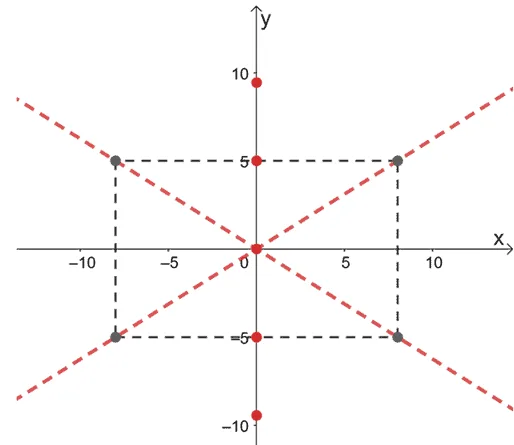 With these guides, we can now plot the hyperbola’s branches opening upward and downward starting from the two vertices.
With these guides, we can now plot the hyperbola’s branches opening upward and downward starting from the two vertices.
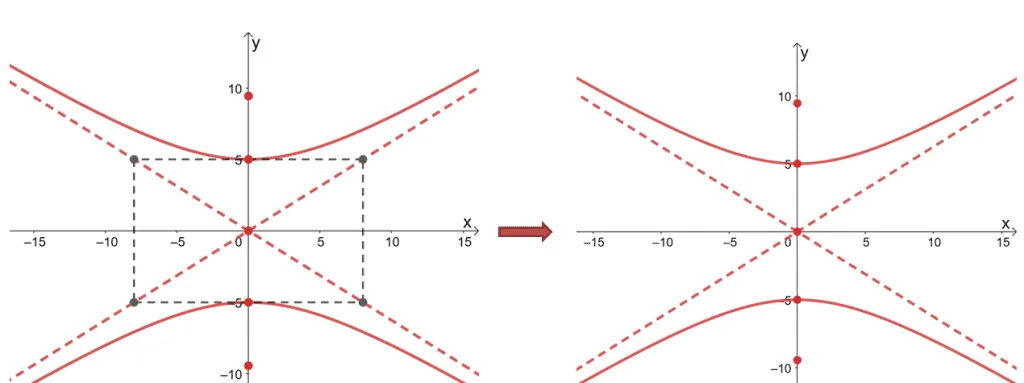
We can finalize the first hyperbola graph by removing the rectangular guide and only leaving the important components behind.
The equation of the second hyperbola, $8x^2 – 50y^2 = 200$, still needs to be written in standard form and we can do this by dividing both sides of the equation by $200$.
\begin{aligned}\dfrac{8x^2}{200} – \dfrac{50y^2}{200} &= \dfrac{200}{200}\\\dfrac{x^2}{25} – \dfrac{y^2}{4} &= 1\end{aligned}
From the standard alone, we can see that the hyperbola’s branches are opening sideward with a center at $(0, 0)$. Let’s go ahead and use the values of $a$ and $b$ to find the vertices and asymptotes of the hyperbola.
$\boldsymbol{a}$ | $\boldsymbol{b}$ | Vertices | Asymptotes |
\begin{aligned}a^2 &= 25\\ a&= 5\end{aligned} | \begin{aligned}b^2 &= 4\\ b&= 2\end{aligned} | \begin{aligned}(-5,0), (5, 0)\end{aligned} | \begin{aligned} y &= \pm \dfrac{b}{a} x \\ y&= \dfrac{2}{5} x\\y&= -\dfrac{2}{5}x\end{aligned} |
We can also determine the hyperbola’s foci by first finding the value of $c$.
\begin{aligned}c^2 &= 25 + 4 \\&= 29\\c&= \sqrt{29}\\&\approx 5.4\\\\\text{foci: }&= (0, -\sqrt{29}), (0, \sqrt{29})\end{aligned}
Plot these components and include a rectangular guide with corners at $(5, 2)$, $(-5, 2)$, $(5, -2)$, and $(-5, -2)$.
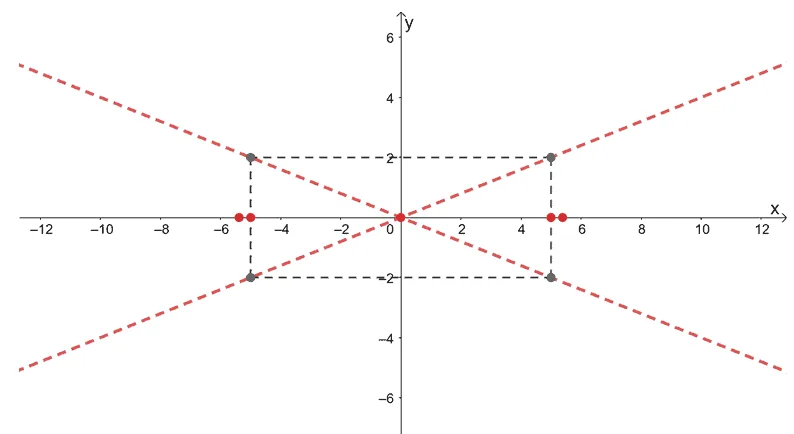
We can now graph the hyperbola’s branches that open sidewards and use the vertices and asymptotes as a guide. Finalize the graph by removing the rectangular guide as shown by the two graphs below.
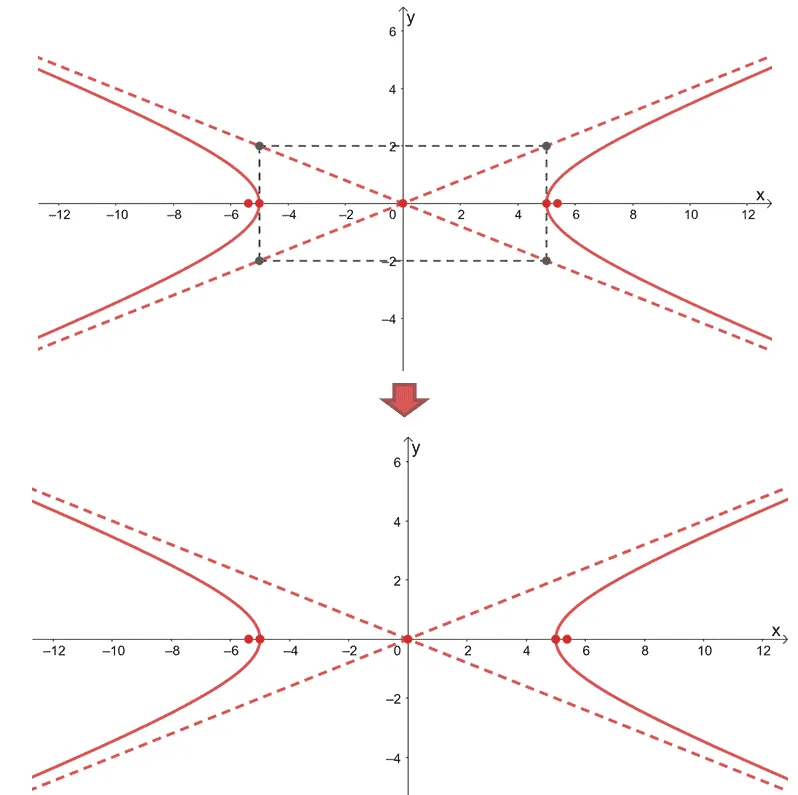
These two graphs are valid – the central rectangle is just a guide, so the final graphs would look better if we remove the rectangular guide.
Example 5
Graph the hyperbola represented by the following equations. Make sure to include the foci, vertices, and asymptotes of the hyperbola as well.
a. $\dfrac{(x + 3)^2}{16} – \dfrac{(y – 2)^2}{9} = 1$
b. $4(y – 1)^2 – 9(x – 3)^2 = 36$
Solution
The hyperbola represented by the first equation has a standard form of $\dfrac{(x – h)^2}{a^2} – \dfrac{(y – k)^2}{b^2} = 1$, where $(h, k)$ represents the hyperbola’s center.
- From the standard form, we can see that the hyperbola opens sideward with a center at $(-3, 2)$.
- This means that we can find its vertices by moving $a$ units to the left and right of the center.
- The hyperbola’s asymptote will be of the form $y – k = \pm \dfrac{b}{a} (x – h)$.
$\boldsymbol{a}$ | $\boldsymbol{b}$ | Vertices | Asymptotes |
\begin{aligned}a^2 &= 16\\ a&= 4\end{aligned} | \begin{aligned}b^2 &= 9\\ b&= 3\end{aligned} | \begin{aligned}(-3 – 4, 2), (-3 + 4, 2) &= (-7,2), (1, 2)\end{aligned} | \begin{aligned} y – k &= \pm\dfrac{b}{a} (x – h)\\y – 2 &= \pm \dfrac{3}{4} (x + 3) \\ y &= 2 \pm \dfrac{3}{4} (x + 3)\end{aligned} |
Let’s find out the distance of the foci from the center by first finding the value of $c$ using $c^2 = a^2 + b^2$.
\begin{aligned}c^2 &= 16 + 9\\&= 25\\c&=5\\\\\text{foci: }&= (-8, 2), (2, 2) \end{aligned}
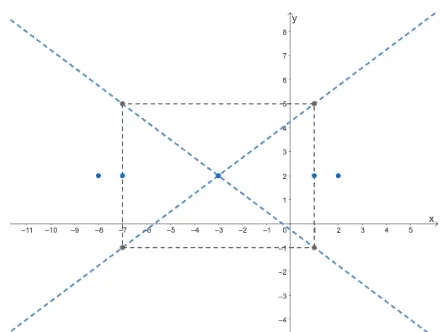
The central rectangle’s general form will also change when the center is translated $h$ units horizontally and $k$ units vertically. The vertices of the rectangle will now be: $\{(h-a, k -b), (h – a, k + b), (h + a, k + b), (h + a, k – b)\}$.
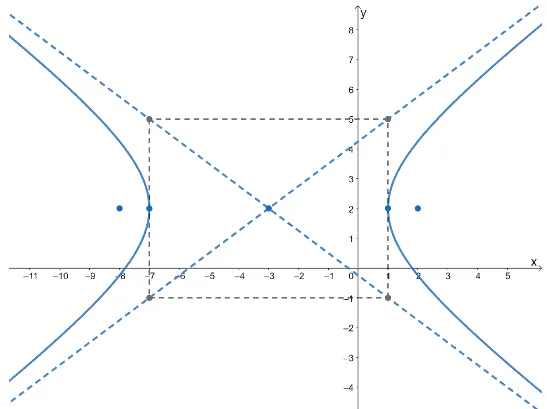
Hence, the vertices of the rectangular guide are $(-7, -1)$, $(-7, 5)$, $(1,5)$, and $(1, -1)$. Let’s now plot this central rectangle as well as the vertices and foci of the hyperbola.
We can plot the hyperbola’s curves by using the vertices and the asymptotes as guides. We’ll show you the graph of the hyperbola with all its important components.
Let’s now work on the second equation, but first, let’s rewrite $4(y – 1)^2 – 9(x – 3)^2 = 36$ in standard form by dividing both sides of the equation by $36$.
\begin{aligned}\dfrac{4(y – 1)^2}{36}– \dfrac{9(x – 3)^2 }{36} &= \dfrac{36}{36}\\\dfrac{(y – 1)^2}{9} – \dfrac{(x – 3)^2 }{4} &= 1 \end{aligned}
Now that the equation is in standard form, we can see that:
- From the standard form, we can see that the hyperbola, with a center at $(3, -1)$, opens upward and downward.
- This means that we can find its vertices by moving $a$ units above and below the center.
- The hyperbola’s asymptote will be of the form $y – k = \pm \dfrac{a}{b} (x – h)$.
$\boldsymbol{a}$ | $\boldsymbol{b}$ | Vertices | Asymptotes |
\begin{aligned}a^2 &= 9\\ a&= 3\end{aligned} | \begin{aligned}b^2 &= 4\\ b&= 2\end{aligned} | \begin{aligned}(3 ,-1 -2), (3 ,-1 +2) &= (3, -3), (3, 1)\end{aligned} | \begin{aligned} y – k &= \pm\dfrac{a}{b} (x – h)\\y – 1 &= \pm \dfrac{a}{b} (x – 3) \\ y &= 1 \pm \dfrac{3}{2} (x – 3)\end{aligned} |
Find the distance of the foci from the center using $c^2 = a^2 + b^2$ then find the foci by adding $c$ units above and below the center.
\begin{aligned}c^2 &= a^2 + b^2\\&= 9 + 4\\&= 13\\c&=\sqrt{13}\\&\approx 3.61\\\\\text{foci: }&=(3, -1-\sqrt{13}), (3, 1 + \sqrt{13})\end{aligned}
Similar with the first hyperbola’s equation, we can determine the central rectangle’s corners by translating the center $2$ units vertically and $3$ units horizontally.
This means that the vertices of the rectangular guide are $(5, -2)$, $(1, 4)$, $(1,-2)$, and $(5, 4)$. Let’s graph these components and then include the hyperbola’s branches using these components as a guide.
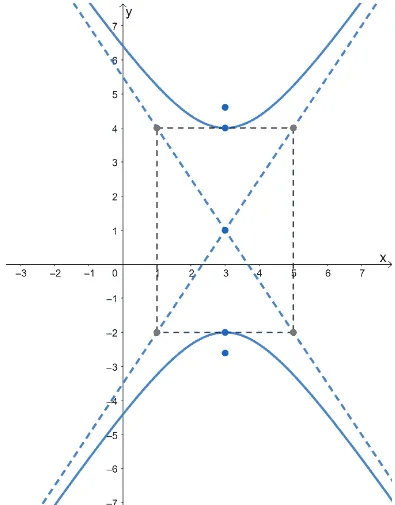
We can finalize the graph of the hyperbola by removing the central rectangle.
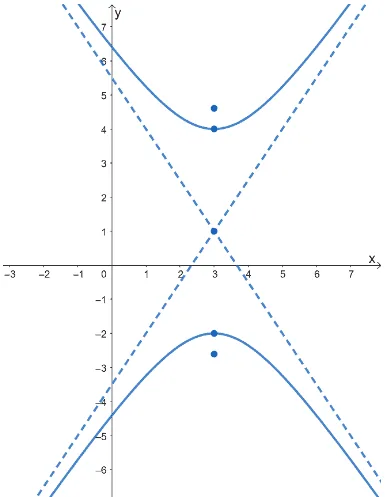
We can see that hyperbolas centered at $(h, k)$ will require similar approaches when we need to graph them from these two graphs. The main difference is that we need to count off the components from a center outside the origin this time.
Example 6
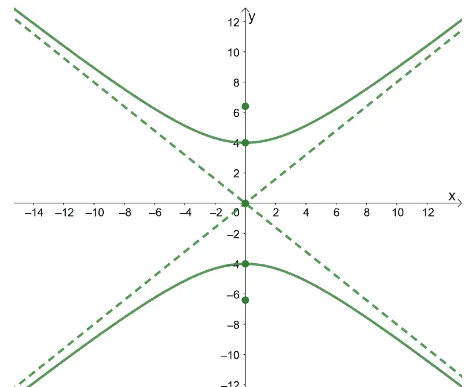
Determine the equation representing the graphs of the hyperbolas shown below.
a.
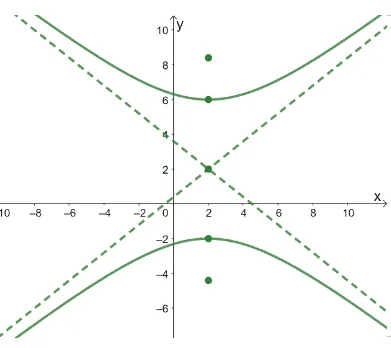
b.
Solution
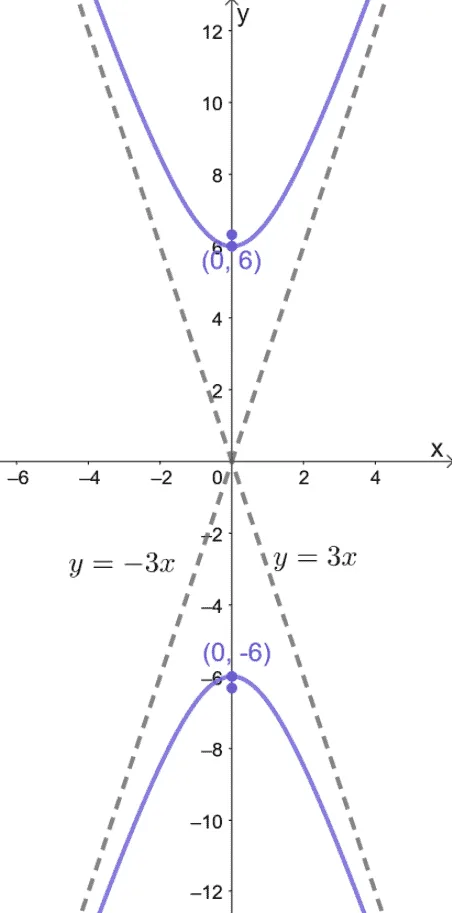
Just by inspection, we can see that the hyperbola is centered at the origin, $(0, 0)$. Since the hyperbola’s branches are opening upward and downward, the standard form of the hyperbola will be $\dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1$.
From the vertices, we can see that $a = 4$ and $a^2 = 16$. For this form, we can see that the asymptotes will have a standard form of $y = \pm \dfrac{a}{b}x $.
We can see that one of the asymptotes passes through the points $(-10, -8)$ and $(10,8)$.
Using this, we can see that the slope of the line is $\dfrac{8- (-8)}{10 – (-10)} = \dfrac{4}{5}$. Equating $\dfrac{4}{5}$ with the slope of the general form, $\dfrac{a}{b}$.
\begin{aligned} \dfrac{4}{5} &= \dfrac{a}{b}\\ \dfrac{4}{5} &= \dfrac{4}{b}\\b&= 5\end{aligned}
This means that $b = 5$ and $b^2 = 25$.
a. We now have $a^2$ and $b^2$, so the equation of the hyperbola is $\dfrac{y^2}{16} – \dfrac{x^2}{25} = 1$.
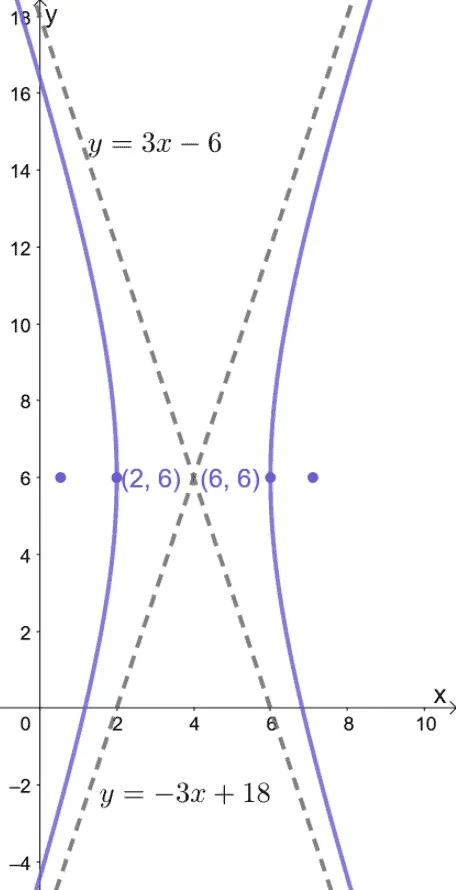
Working on the second graph, we can see that the hyperbola is a translated counterpart of the first hyperbola.
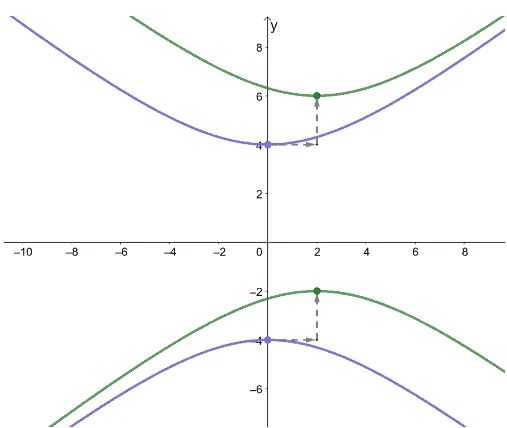
This means that we can use the first hyperbola’s standard form and modify it to highlight the translations.
- The second hyperbola is the result of the hyperbola being translated $2$ units to the left.
- Also, it’s translated $2$ units upward.
Hence, the center is located at $(2, 2)$ and the hyperbola’s standard form will be $\dfrac{(y – k)^2}{a^2} – \dfrac{(x – h)^2}{b^2} = 1$.
b. Using the value of $(h, k)$ as $(2, 2)$, the equation of the translated hyperbola is $\dfrac{(y – 2)^2}{a^2} – \dfrac{(x – 2)^2}{b^2} = 1$.
Another way of answering the second problem is to start from scratch and use a similar approach to the first one – you can try doing this method, but translating when possible, is a much faster approach.
These two examples show that we can work backward and find a hyperbola equation based on its graph.
Practice Questions
![]()
Open Problems
1. Identify the center, vertices, and foci of the following hyperbolas.
a. $\dfrac{y^2}{49} – \dfrac{x^2}{32} = 1$
b. $\dfrac{x^2}{25} – \dfrac{y^2}{144} = 1$
c. $\dfrac{(x – 8)^2}{4} – \dfrac{(y + 6)^2}{5} = 1$
d. $\dfrac{(y + 3)^2}{81} – \dfrac{(x – 2)^2}{63} = 1$
2. Graph the hyperbola represented by the following equations. Make sure to include the foci, vertices, and asymptotes of the hyperbola as well.
a. $\dfrac{(y + 5)^2}{36} – \dfrac{(x – 5)^2}{64} = 1$
b. $36(x – 4)^2 – 4(y – 6)^2 = 144$
Open Problem Solutions
1.
Center | Vertices | Foci | |
a. | $(0, 0)$ | $(0, -7)$, $(0, 7)$ | $(0, -9)$, $(0, 9)$ |
b. | $(0, 0)$ | $(-5, 0)$, $(5, 0)$ | $(-13, 0)$, $(13, 0)$ |
c. | $(8, -6)$ | $(6, -6)$, $(10, -6)$ | $(5, -6)$, $(11, -6)$ |
d. | $(2, -3)$ | $(2, -12)$, $(2, 6)$ | $(2, -15)$, $(2, 9)$ |
2.
a.
b.
Images/mathematical drawings are created with GeoGebra.
