- Home
- >
- Vector multiplication – Types, Process, and Examples
Vector multiplication – Types, Process, and Examples
 Vector multiplication helps us understand how two vectors behave when combined. This vector operation has an extensive application in physics, engineering, and astronomy, so we need to learn about these techniques, especially if we study higher maths.
Vector multiplication helps us understand how two vectors behave when combined. This vector operation has an extensive application in physics, engineering, and astronomy, so we need to learn about these techniques, especially if we study higher maths.
Vector multiplication covers two important techniques in vector operations: scalar product and cross product.
Learning about vector multiplication can also help us refresh our knowledge of vectors and vector application topics.
This article will discuss the two types of vector multiplication and learn the difference between the two. Make sure to keep your notes on the following concepts handy since we may have to brush up on them while learning about vector multiplication.
- Understand the different components that make up a vector.
- Review how we add and subtract vectors.
- Understand how a scalar factor affects a given vector.
For now, let’s go ahead and learn the two important techniques of vector multiplication.
How to multiply vectors?
When we multiply two or more vectors, it is important to determine whether we want a product that has a scalar quantity or vector quantity. The technique we’ll need to apply depends on our answer to that question.
There are actually three possible products in vector multiplication: vector multiplied by a scalar factor, the dot (or scalar) product, and the cross (or vector) product.
- At this point, we should have learned about distributing scalar factors to a vector, and that’s the first procedure. Make sure the check the links we’ve included in the first section.
- The dot product or known as the scalar product, as you have guessed, returns a scalar quantity.
- Similarly, the cross product returns a vector quantity.
Our discussion will focus on the latter two techniques: dot and cross products. These names will help you identify the operation that needs to be done since their operators represent a dot ($\cdot$) and a cross symbol($\times$), respectively.
What are the vector multiplication rules?
The two products will have different results and processes. This is why we need to understand what the dot and cross products represent.
Dot Product and Its Rules
The dot product represents the projection of one vector onto another vector. Let’s say we have $\overrightarrow{A}$ and $\overrightarrow{B}$, the dot product of $\overrightarrow{A}$ and $\overrightarrow{B}$ is simply the projection of $\overrightarrow{A}$ onto the vector $\overrightarrow{B}$.
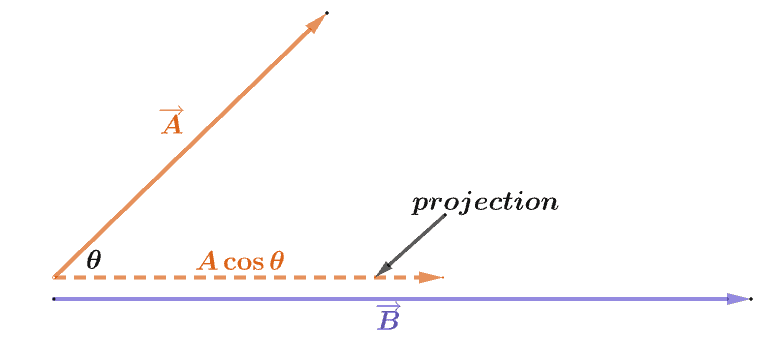
Here’s a visualization of what happens when we find the dot product of $\overrightarrow{A}$ and $\overrightarrow{B}$. What happens is we use the vector component of $\overrightarrow{A}$ along the direction of $\overrightarrow{B}$ and multiply that component with the magnitude of $\overrightarrow{B}$.
\begin{aligned}\overrightarrow{A} \cdot \overrightarrow{B} &= (A \cos \theta)(B)\\&= AB\cos \theta\end{aligned}
This means that the dot product of $\overrightarrow{A}$ and $\overrightarrow{B}$ ($\overrightarrow{A} \cdot \overrightarrow{B})$ is simply the product of the two vectors’ magnitudes and the cosine of the angle between them.
The resulting product is scalar, so the dot product is also known as the scalar product. Here are some important properties to keep in mind about the scalar product:
- The scalar product is commutative: $\overrightarrow{A} \cdot \overrightarrow{B} = \overrightarrow{B} \cdot \overrightarrow{A}$.
- The scalar product is distributive: $\overrightarrow{A} \cdot (\overrightarrow{B} +\overrightarrow{C}) = \overrightarrow{B} \cdot (\overrightarrow{A} +\overrightarrow{C})$.
- The scalar product of two perpendicular vectors will always be equal to $0$ (that’s because $\cos 90^{\circ}$ is equal to $0$).
There’s another way to calculate the two vectors’ dot product: we multiply their respective Cartesian components. Let’s say $\mathbf{i}$, $\mathbf{j}$, and $\mathbf{k}$ are the unit vectors along the $x$, $y$, and $z$ axes, respectively, we can find the product of $\overrightarrow{A}$ and $\overrightarrow{B}$ as shown below.
\begin{aligned}\overrightarrow{A} &= A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}\\\overrightarrow{B} &= B_1\mathbf{i} + B_2\mathbf{j}+ B_3\mathbf{k}\\\\\overrightarrow{A} \cdot \overrightarrow{B}&=A_1B_1 + A_2B_2 +A_3B_3 \end{aligned}
We can calculate these two ways for the dot product (or scalar product) of two vectors. Now, let’s move on to the second important result of vector multiplication: the cross or vector product.
Cross Product and Its Rules
You might already see a pattern here- for cross products, we use the operator $\times$, and the resulting product is a vector. Because of this, the cross or vector product expects us to consider the direction.
A great way to visualize two vectors’ cross product is by determining the area of the parallelogram by the vectors.
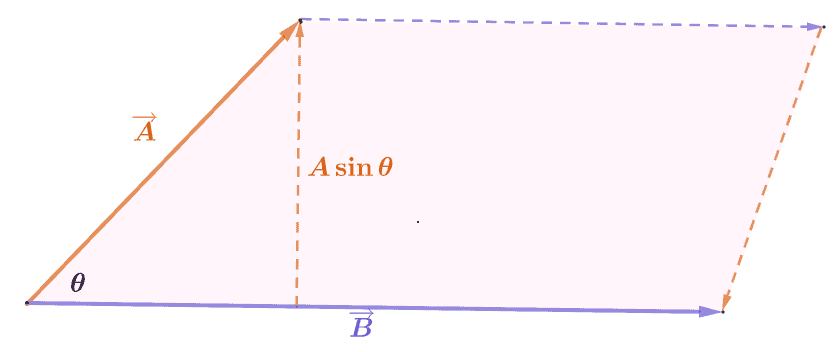
From this, we can see that the cross product of $\overrightarrow{A}$ and $\overrightarrow{B}$ is equal to the product of $A\sin \theta$ and $\overrightarrow{B}$.
\begin{aligned}\overrightarrow{A} \times \overrightarrow{B} &= (A \sin \theta)(B)\\&= AB \sin \theta \mathbf{n} \end{aligned}
Keep in mind that $\mathbf{n}$ is simply the unit vector that is perpendicular to both $\overrightarrow{A}$ and $\overrightarrow{B}$. This means that we can find the cross product by multiplying the two vectors’ magnitudes when given two vectors and the angle between them. We can then multiply the result by the sine of the angle between the two vectors.
Here are some important properties of vector or cross products that may come in handy:
- Vector or cross products are anti-commutative: $\overrightarrow{A} \times \overrightarrow{B} = -\overrightarrow{B} \times \overrightarrow{A}$.
- Vector product is distributive over addition: $\overrightarrow{A} \times (\overrightarrow{B}\times \overrightarrow{C}) = \overrightarrow{A} \times \overrightarrow{B} + \overrightarrow{A} \times \overrightarrow{C}$.
- The cross product of two parallel vectors will always be equal to $0$.
As with dot products, we can also find the vector product of two vectors given their Cartesian forms. Using the same unit vectors, we have $\overrightarrow{A} = A_1\mathbf{i} + A_2\mathbf{j}+ A_3\mathbf{k}$ and $\overrightarrow{B} = B_1\mathbf{i} + B_2\mathbf{j}+ B_3\mathbf{k}$.
An important property to observe is the vector products of the three-unit vectors. We’ve summarized the products for you here:
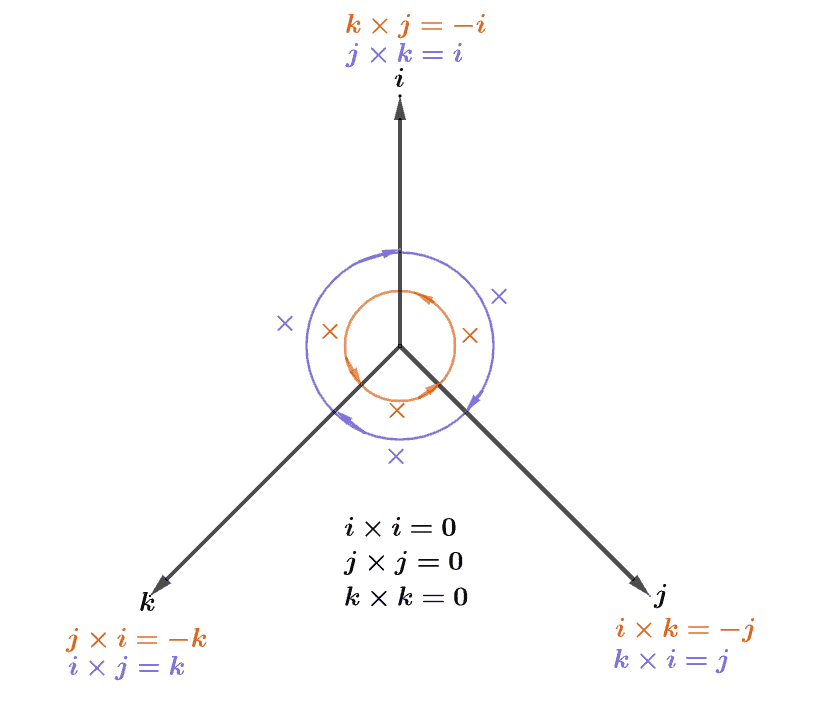
We can develop the cross-product formula by distributing the two vectors over addition and using the cross-products of the unit vectors. However, to keep this discussion straightforward, here’s how we can calculate for the vector product of $\overrightarrow{A}$ and $\overrightarrow{B}$.
\begin{aligned}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k}\end{aligned}
If you have already studied determinants in the past, there’s another way of understanding the vector product, and you may help you remember the operation as well.
- We can write the unit vectors on the first array.
- The two vectors’ components in the next two arrays.
- To find the coefficient before $\mathbf{i}$, we find the determinant of the remaining $2\times2$ matrix once we cover the row and column that contains $\mathbf{i}$.
- Apply a similar process to find the components for $\mathbf{j}$and $\mathbf{k}$.
\begin{aligned}\overrightarrow{A} \times \overrightarrow{B}&=\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ A_1 & A_2 & A_3\\B_1 & B_2 & B_3\end{vmatrix}\\&=\begin{vmatrix} A_2 & A_3\\B_2 & B_3\end{vmatrix}\mathbf{i}- \begin{vmatrix} A_1 & A_3\\B_1 & B_3\end{vmatrix}\mathbf{j}+\begin{vmatrix} A_1 & A_2\\B_1 & B_2\end{vmatrix}\mathbf{k}\\&=(A_2B_3 – A_3B_2)\mathbf{i} -(A_1B_3 – A_3B_1)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k}\end{aligned}
Regardless of the approach, it should still return the same results. That’s all we need to learn so far about vector multiplication, so why don’t we go ahead and try out these problems below to better understand cross-products and dot products?
Example 1
In Physics, the work done on an object can be calculated using the formula, $\overrightarrow{F} \cdot \overrightarrow{s}$, where the $\overrightarrow{F}$ represents the Force (in Newtons, N) and $s$ represents the resulting displacement (its magnitude is in meters, m).
What is the work done on the object with the following components?
a. $|\overrightarrow{F}| = 2$ N, $|\overrightarrow{s}| = 6$ m, and $\theta = 30^{\circ}$
b. $|\overrightarrow{F}| = 12$ N, $|\overrightarrow{s}| = 2.5$ m, and $\theta = 0^{\circ}$
c.$|\overrightarrow{F}| = 200$ N, $|\overrightarrow{s}| = 3$ m, and $\theta = 60^{\circ}$
Solution
This problem requires us to multiply the magnitudes of $\overrightarrow{F}$ and $\overrightarrow{s}$ and the cosine of the angle formed, $\theta$. In short, we need the dot product of $|\overrightarrow{F}| $ and $|\overrightarrow{s}| .
\begin{aligned}\overrightarrow{F} \cdot \overrightarrow{s} &= |\overrightarrow{F}||\overrightarrow{s}|\cos \theta \end{aligned}
We’ll use the same formula for all three values so, we’ll go ahead and summarize the calculations in one table.
| a. | \begin{aligned}\overrightarrow{F} \cdot \overrightarrow{s} &=(2)(6)\cos 30^{\circ}\\&= 12 \cdot \dfrac{\sqrt{3}}{2}\\&=6\sqrt{3} \end{aligned} | \begin{aligned}\overrightarrow{F} \cdot \overrightarrow{s} &=6\sqrt{3} \text{N}\cdot\text{m}\\\approx10.39\text{N}\cdot\text{m} \end{aligned} |
| b. | \begin{aligned}\overrightarrow{F} \cdot \overrightarrow{s} &=(12)(2.5)\cos 0^{\circ}\\&= 30 \cdot 1\\&= 30 \end{aligned} | \begin{aligned}\overrightarrow{F} \cdot \overrightarrow{s} &=30 \text{N}\cdot\text{m}\end{aligned} |
| c. | \begin{aligned}\overrightarrow{F} \cdot \overrightarrow{s} &=(200)(3)\cos 60^{\circ}\\&= 600 \cdot \dfrac{1}{2}\\&=300 \end{aligned} | \begin{aligned}\overrightarrow{F} \cdot \overrightarrow{s} &=300 \text{N}\cdot\text{m}\end{aligned} |
This is a great way to apply our dot product formula and also get a glimpse of one of the many applications of vector multiplication.
Example 2
Find the expressions for $\overrightarrow{A} \cdot \overrightarrow{B}$ and $\overrightarrow{A} \times \overrightarrow{B}$ given the following vectors:
\begin{aligned} \overrightarrow{A} &= 2\mathbf{i} – 3\mathbf{j}\\\overrightarrow{B} &=3\mathbf{i}+ 2\mathbf{j}\end{aligned}
Solution
When given the Cartesian forms of the vectors, we can still find their dot and cross products.
- We can multiply the corresponding components’ coefficients then add the products to find the dot product.
- For the cross product with the form,$a\mathbf{i} + b\mathbf{j}$, we distribute the terms algebraically and cancel out cross products of the same unit vectors.
Why don’t we work with $\overrightarrow{A} = 2\mathbf{i} – 3\mathbf{j}$ and $\overrightarrow{B} =3\mathbf{i} + 2\mathbf{j}$ first to understand the process better?
The dot product will be straightforward – we multiply the coefficients before $\mathbf{i}$ and $\mathbf{j}$.
\begin{aligned}\overrightarrow{A} \cdot\overrightarrow{B}&= ({\color{blue}2}\mathbf{i} – {\color{red}3}\mathbf{j}) \cdot ({\color{blue}3}\mathbf{i} + {\color{red}2}\mathbf{j})\\&= ({\color{blue}2})({\color{blue}3}) + ({\color{red}-3})({\color{red}2})\\&= 6 – 6\\&= 0\end{aligned}
This means that the dot product of $\overrightarrow{A}$ and $\overrightarrow{B}$ is equal to $0$.
Since the vector product is distributive over addition, what we can do is distribute the terms algebraically and cancel out $\mathbf{i}\times\mathbf{i}$ or $\mathbf{j}\times\mathbf{j}$.
\begin{aligned}\overrightarrow{A} \times\overrightarrow{B}&= (2\mathbf{i} – 3\mathbf{j}) \times (3\mathbf{i} + 2\mathbf{j})\\&= (2\mathbf{i})\times (3\mathbf{i} + 2\mathbf{j}) – 3\mathbf{j}\times (3\mathbf{i} + 2\mathbf{j})\\&= [(2)(3) \mathbf{i}\times\mathbf{i} +(2)(2) \mathbf{i}\times\mathbf{j}]+[(-3)(3) \mathbf{j}\times\mathbf{i} + (-3)(2)\mathbf{j}\times\mathbf{j}]\end{aligned}
Recall that identical vectors’ cross product will be equal to zero, so let’s use this to cancel out terms. Also, review the guide we provided for the cross-products of other unit vectors.
\begin{aligned}\overrightarrow{A} \times\overrightarrow{B}&= (0 + 4\mathbf{k})+(-9(\mathbf{-k} )+ 0) \\&= (4 + 9)\mathbf{k}\\&= 13\mathbf{k}\end{aligned}
Hence, we’ve shown how we can find the cross and dot products of two vectors of the form, $a\mathbf{i} + b\mathbf{j}$.
Example 3
Evaluate the following expressions given the Cartesian forms of the three vectors shown below.
\begin{aligned} \overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4\mathbf{j}- 3\mathbf{k}\\\overrightarrow{C} &=3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k}\end{aligned}
a. $\overrightarrow{A} \times\overrightarrow{B}$
b.$\overrightarrow{B}\cdot (\overrightarrow{A}\times\overrightarrow{B})$
c. $(\overrightarrow{A} \times \overrightarrow{B})\times \overrightarrow{C}$
Solution
There are two ways for us to find the cross product of $\overrightarrow{A}$ and $\overrightarrow{B}$: by using the formula derived from distributing the two vectors or using our knowledge on determinants. We’ll use the first option for now:
\begin{aligned}\overrightarrow{A} \times \overrightarrow{B}&=(A_2B_3 – A_3B_2)\mathbf{i} +(A_3B_1 – A_1B_3)\mathbf{j}+(A_1B_2 – A_2B_1)\mathbf{k}\end{aligned}
Hence, we have the cross product of the two vectors:
\begin{aligned}\overrightarrow{A} &= 4\mathbf{i} – 5\mathbf{j} + 6\mathbf{k}\\\overrightarrow{B} &=-2\mathbf{i}+ 4\mathbf{j}- 3\mathbf{k}\\\overrightarrow{A} \times \overrightarrow{B}&=(-5\cdot -3 – 6\cdot 4)\mathbf{i} +(-3\cdot 4 – 4\cdot -3)\mathbf{j}+(4\cdot 4 – -5\cdot -2)\mathbf{k}\\&=-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}\\&=-9\mathbf{i} +6\mathbf{k}\end{aligned}
We’ll be using this result for the next two problems, so let’s assign $\overrightarrow{M}$ to represent $-9\mathbf{i}+0\mathbf{j}+6\mathbf{k}$ or $-9\mathbf{i} +6\mathbf{k}$.
To find $\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B})$, we simply multiply the coefficients of the corresponding unit vectors of both $\overrightarrow{A}$ and that of the resulting vector,$\overrightarrow{M}$.
\begin{aligned}\overrightarrow{B} \cdot(\overrightarrow{A}\times\overrightarrow{B}) &=\overrightarrow{B}\cdot\overrightarrow{M}\\&=(-2\mathbf{i}+ 4\mathbf{j}- 3\mathbf{k})\cdot(-9\mathbf{i}+0\mathbf{j}+6\mathbf{k})\\&= (-2)(-9)+ (4)(0) +(-3)(6)\\&=18-18\\&=0\end{aligned}
For the third problem, let’s find the cross product of $(\overrightarrow{A} \times \overrightarrow{B}) = \overrightarrow{M}$ and $\overrightarrow{C}$ by taking the determinants of the coefficients.
\begin{aligned}(\overrightarrow{A}\times\overrightarrow{B}) \times \overrightarrow{C} &=\overrightarrow{M}\times\overrightarrow{C}\\&=(-9\mathbf{i}+0\mathbf{j}+6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})\end{aligned}
Let’s rewrite these in matrix form and start calculating the determinants of the resulting $2\times2$ matrices as shown below.
\begin{aligned}(-9\mathbf{i}+ 0\mathbf{j} +6\mathbf{k})\times(3\mathbf{i}+ 2\mathbf{j}- 6\mathbf{k})&=\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ -9 & 0 & 6\\3 & 2 & -6\end{vmatrix}\\&=\begin{vmatrix} 0 & 6\\2 & -6\end{vmatrix}\mathbf{i}-\begin{vmatrix} -9 & 6\\3 & -6\end{vmatrix}\mathbf{j}+\begin{vmatrix} -9 & 0\\3 & 2\end{vmatrix}\mathbf{k}\\&=(0 – 12)\mathbf{i} -(54 – 18)\mathbf{j}+(-18- 0)\mathbf{k}\\&=-12\mathbf{i} -36\mathbf{j}-18\mathbf{k}\end{aligned}
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
