Intersecting Lines – Explanations & Examples

Now that you’re taking geometry or precalculus classes, you’ll be bumping into the concepts of intersecting lines multiple times. This is why we need to understand the concepts related to intersecting lines.

For now, let’s dive into a quick definition of intersecting lines:

                                   Intersecting lines are lines that meet each other at one point.

It’s amazing how a simple definition can lead us to know important properties about linear equations’ angles and systems. This article will help us understand the definition, properties, and applications of intersecting lines.

Intersecting lines definition

Intersecting lines are two or more lines that are coplanar to each other and meet at a common point.

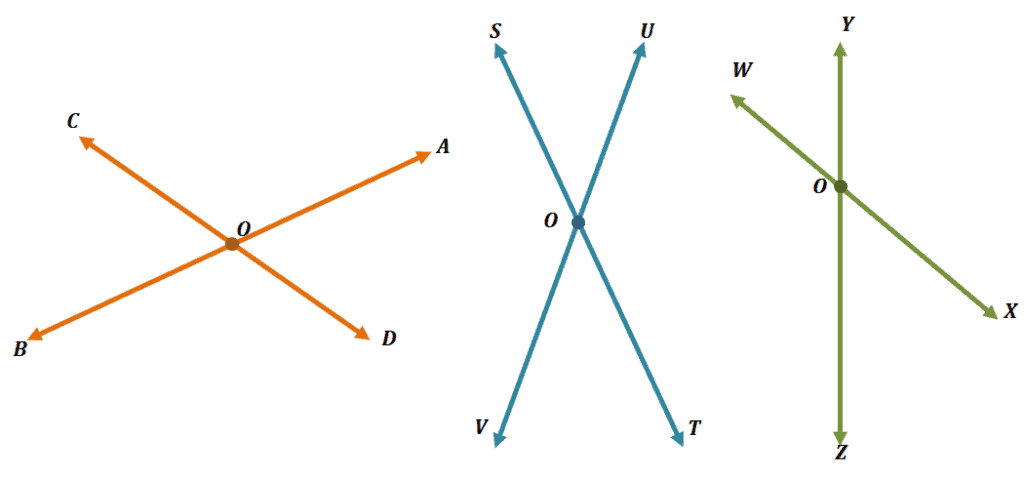
The three pairs of lines shown above are examples of intersecting lines. See how each pair intersects at Point $\boldsymbol{O}$? We call this the point of intersection. Line segments can also intersect and have a point of intersection.

Keep in mind that three or more lines can share more than one point of intersection.

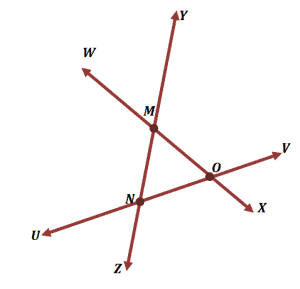
Lines $\overline{WX}$,$\overline{YZ}$, and $\overline{UV}$  intersect each other, and as can be seen, there are three points of intersection shared by the lines.

• Lines $\overline{WX}$ and $\overline{UV}$ intersect at Point $\boldsymbol{O}$.
• Lines $\overline{YZ}$and $\overline{UV}$ intersect at Point $\boldsymbol{N}$.
• Lines $\overline{WX}$ and $\overline{YZ}$ intersect at Point $\boldsymbol{M}$.

The angles formed by these intersecting lines (and line segments) have interesting properties that we’ll soon learn in the next few sections.

What are some real-world examples of intersecting lines?

One way to test our understanding of intersecting lines’ definition is to think of real-world examples representing intersecting lines. Can you think of any? Here are three that can help you list down more examples:

• Our scissors are great examples of objects that are intersecting each other and sharing a common point.
• Crossroads also represent intersecting lines as well since they meet at intersecting points.
• The lines of floors intersect each other as well and share points of intersection.

How do we use intersecting lines in coordinate geometry?

Want to learn what it means when two lines or curves intersect in coordinate geometry? Below are just some of the properties that we’ll learn about intersecting lines on an xy-coordinate system.

• When two graphs of two functions intersect each other, the intersection point represents the solution when both functions are equated to each other.
• This also means that when two lines or graphs intersection, then their equation will have a solution.
• Lines that intersect with the $x$ and $y$-axis contain point/s of intersection, and these represent the graph’s $x$ and $y$-intercepts, respectively.

We’ll learn more about all these essentials concepts when we dive deeper into functions and solve functions by using graphs.

For now, let’s observe the properties shared by angles found at the point of intersection. In the next sections, we’ll also learn how to apply them in solving word problems that involve angles and intersecting lines.

Properties of the angles formed by intersecting lines

When two or more lines intersect, they form different angles at the point of intersection.

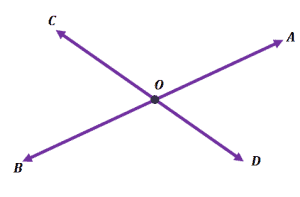
Lines $\overline{AB}$ and $\overline{CD}$, for example, meet at Point $\boldsymbol{O}$. They also form four angles at the point of intersection: $\angle COA$, $\angle COB$, $\angle BOD$, and $\angle AOD$.

Have you also noticed two pairs of vertical angles? If you need a refresher on what vertical angles are, you can check out this article we wrote before on vertical angles. For the case of the two intersecting lines shown above, we have the following vertical angles:

• $\angle COA$ and$\angle BOD$
• $\angle COB$ and $\angle AOD$

The properties of vertical and linear angles still apply to the angles formed by two intersecting lines.

What happens with the angles when a third line intersects the two intersecting lines in the middle?

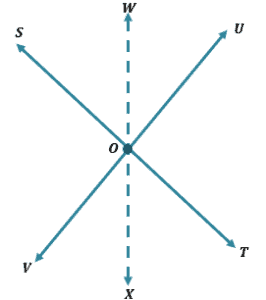
The same properties apply, and by the angle addition postulate, the angle intersected by the third intersecting line will create two angles that will add up to the measure of the intersected angle.

• This means that the sum of $\boldsymbol{\angle SOW}$ and $\boldsymbol{\angle WOU}$ is equal to $\boldsymbol{\angle SOU}$.
• Similarly, $\boldsymbol{\angle VOX + \angle XOT = \angle VOT}$.

Want to test these concepts out? You can try constructing four intersecting lines and test out how the angles behave.

Now that we’ve learned about intersecting lines’ definitions and properties, it’s time for us to work on some questions to check our knowledge.

Example 1

Complete the following statements with either sometimes, never, and always.

1. Parallel lines can ____________ be intersecting lines.
2. Perpendicular lines can ____________ be intersecting lines.
3. The hands of a clock can ____________ represent two intersecting lines.
4. Intersecting lines will ______________ have more than one point of intersection.

Solution

When working with questions like this, it’s always helpful to go back to defining the terms that are involved.

• Parallel lines are lines that will never meet, so they will never.
• Perpendicular lines, on the other hand, form 90° together, so they will always.
• The hands of a clock intersect at a common point will always represent two intersecting lines.
• For three or more intersecting lines, they may sometimes share two or more intersecting points.

Example 2

Which of the following statements is not true?

1. Three intersecting lines can share a common point of intersection.
2. Two intersecting lines form two pairs of vertical angles.
3. Two intersecting lines form four pairs of vertical angles.
4. Three intersecting lines can never share four common points of intersection.

Solution

Let’s go ahead and look into each of the given statements.

• It is possible for three intersecting lines to only intersect at one common point, so the statement is true.
• When two lines intersect, they form four angles. Each pair of angles opposite each other are vertical angles, so this statement is true.
• Two intersecting lines form four angles and two pairs of vertical angles only. This statement is false.
• The maximum number of intersecting points present between the three intersecting lines is three, so it’s impossible to have four common points. Hence, the fourth statement is true.

Example 3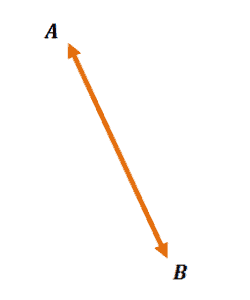

Construct a line that will intersect Line $\overline{AB}$. Label the line and intersection point, then name four angles formed by the two intersecting lines.

Solution

Construct a second line that intersects Line $\overline{AB}$. Below are three pairs of intersecting lines to guide you in creating your own pair of intersecting lines.

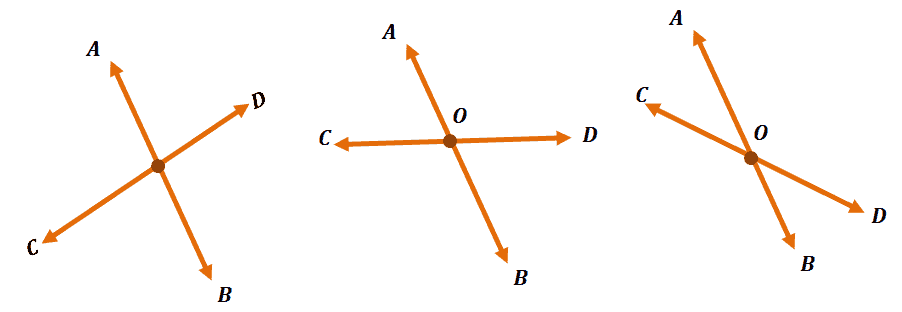
In the three examples, we named the intersecting line $\overline{CD}$ and the point of intersection Point $O$. Your solution may look different from the ones shown above, but no worries, they are all good as long as the two lines intersect.

The four angles formed for the intersecting lines are $\angle AOC$, $\angle AOD$, $\angle COB$, and $\angle BOD$. If you labeled your lines differently, you’d have a different answer than what we’ve shown.

How do you know if your answer is correct? Check if the names of all the angles have the same letter in the middle.

Example 4

It will be impossible to create four intersecting lines that only share one point of intersection.

Prove the statement wrong by constructing a counterexample.

Solution

Construct four intersecting lines where all meet at one common point.

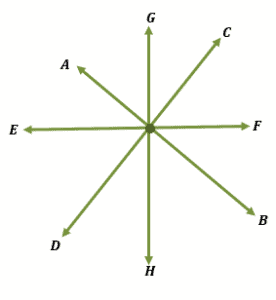
The example above is one possible counterexample for the statement. Feel free to construct your own to show that the statement is not true.

Use the image shown below to answer questions 5 – 7.

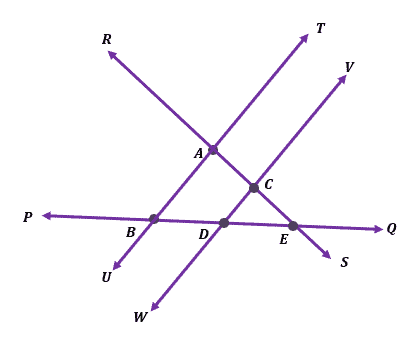
Example 5

Name two pairs of intersecting lines and their corresponding points of intersection.

Solution

Here are some pairs of lines that you may discover from the image, and we’ve included their points of intersection.

• Lines $\overline{RS}$ and $\overline{TU}$ intersecting at Point $\boldsymbol{A}$.
• Lines $\overline{PQ}$ and $\overline{VW}$ intersecting at Point $\boldsymbol{D}$.
• Lines $\overline{PQ}$ and $\overline{TU}$ intersecting at Point $\boldsymbol{B}$.
• Lines $\overline{PQ}$ and $\overline{RS}$ intersecting at Point $\boldsymbol{E}$.
• Lines $\overline{VW}$ and $\overline{RS}$ intersecting at Point $\boldsymbol{C}$.

Were you able to find two pairs from the list we have? Try to locate the remaining three to help you master this concept!

Example 6

Name three line segments that share a common point of intersection.

Solution

Remember that line segments can also intersect. Here are two examples of three line segments sharing a common intersection point.

• Line segments $\overline{AC}$, $\overline{DC}$, and $\overline{EC}$ intersecting at Point $\boldsymbol{C}$.
• Line segments $\overline{BD}$, $\overline{CD}$, and $\overline{ED}$ intersecting at Point $\boldsymbol{D}$.

When dealing with problems like this, start by finding three line segments within the intersecting lines. Make sure that they share a common intersecting point.

Example 7

What are the two intersecting lines that form $\angle UAS$ and $\angle RAT$? If $\angle UAS$ is equal to $68^{\circ}$, what would the value of $\angle RAT$ be?

Solution

A trick to remember is that the two vertical angles formed by a pair of intersecting lines will meet at their common point of intersection. This means that the angles’ intersection is found at Point $\boldsymbol{A}$.

This will help you find the two lines that intersect at Point $\boldsymbol{A}$. Hence, we have lines $\overline{RS}$ and $\overline{TU}$.

Since vertical angles will always be equal, by definition, $\angle UAS = \angle RAT = 68^{\circ}$.

Example 8

Lines $\overline{AD}$ and $\overline{BC}$ are two intersecting lines that meet at Point $\overline{O}$.

1. What are the four angles formed by the intersecting lines?
2. List down two pairs of vertical angles formed by the two vertical lines?
3. If $\angle AOC = (2x + 10)^{\circ}$ and $\angle BOD = (3x – 40)^{\circ}$, what is the angle measure of $\angle BOA$?

Solution

Construct the two intersecting lines with $\boldsymbol{O}$ as its point of intersection.

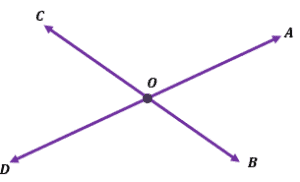
You can see four angles formed at the point of intersection. These angles are: $\angle AOC$, $\angle BOD$, $\angle AOB$, and $\angle COD$.

Observe the two pairs of vertical angles – each pair facing opposite each other.

This means that the two pairs of vertical angles are:

• $\angle AOC$ and $\angle BOD$
• $\angle AOB$ and $\angle COD$

Since $\angle AOC$ and $\angle BOD$ are vertical angles, their angle measures are equal. We can equate both expressions to solve for $x$.

$\begin{aligned} 2x + 10 &= 3x – 40\\ -x &= -50\\ x &= 50\end{aligned}$

Let’s now find the measure of $\angle AOC = 2(50) + 10 = 110^{\circ}$. Since we’re being asked to find $\angle BOA$, we can subtract the value of $\angle AOC$ from $180 ^{\circ}$. Hence, $\angle BOA = 70^{\circ}$.

When working with intersecting lines and word problems involving them, always go back to its fundamental definition and properties. Try out some more practice problems below to further harness your knowledge on intersecting lines.