- Home
- >
- Negative reciprocal – Explanation and Examples
JUMP TO TOPIC
Negative reciprocal – Explanation and Examples
 Negative reciprocal may sound complicated, but once we’ve understood its concept, you’ll see how easy it is to apply and find a number’s negative reciprocal. Why don’t we dissect the two words?
Negative reciprocal may sound complicated, but once we’ve understood its concept, you’ll see how easy it is to apply and find a number’s negative reciprocal. Why don’t we dissect the two words?
Negative and reciprocal – this means that a number’s negative reciprocal is the result of multiplying the number’s reciprocal by $\mathbf{-1}$.
As straightforward as its definition, negative reciprocals have a wide range of applications that include finding perpendicular slopes and modeling real-world applications that make use of inverse relationships.
What is a negative reciprocal?
When dealing with negative reciprocals, we’ll first recall what these two words represent in math: negative and reciprocal.
$ \boldsymbol{\dfrac{a}{b} \rightarrow – \dfrac{b}{a} }$
We’ll slowly break down this form, and by the end of this article, you’ll definitely be able to understand what this represents.
Reciprocal
The reciprocal of a number or a function is the value or expression that results from reversing the numerator and denominator’s places.
$ \boldsymbol{\dfrac{a}{b}\rightarrow \dfrac{b}{a} }$
Reciprocals are considered multiplicative inverses since they will always be 1 when we multiply a number by its reciprocal.
$ \dfrac{a}{b} \cdot \dfrac{b}{a}=1$
Master your knowledge on reciprocals here.
Negative of a Number (or a Function)
The negative of a number or a function is the result of a number being multiplied by -1. Let’s say we have a fraction, $\dfrac{b}{a}$, its negative counterpart will be $-\dfrac{b}{a}$.
$ \boldsymbol{-1 \cdot \dfrac{b}{a} = -\dfrac{b}{a}}$
Learn more about negative numbers here.
When we combine these two concepts, we’ll have the negative reciprocal of a number. This means that negative reciprocals result from us taking the reciprocal of a number then find the negative value of the result.
Hence, we have $ \boldsymbol{\dfrac{a}{b} \rightarrow – \dfrac{b}{a} }$.
How to find negative reciprocal?
Now that we understand what negative reciprocals represent, how do we manipulate different forms of expressions to have their negative reciprocals?
- Always begin by switching the places of the numerator and the denominator of the fraction.
- Once we have the reciprocal, multiply the result by $\mathbf{-1}$.
We’ve created quick guides you can note when working with different types of numbers and expressions.
Let’s start by learning to find the negative reciprocal of a fraction, $\dfrac{a}{b}$, where $b \neq 0$.

What if we’re working with rational functions such as $\dfrac{p(x)}{q(x)}$? We apply the same process as we did with fractions.
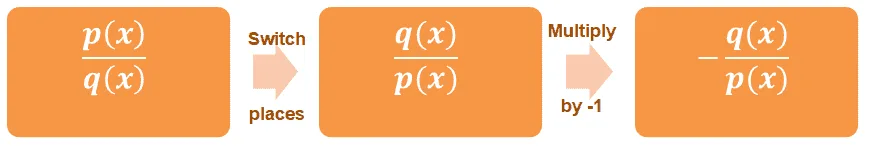
The rational function and its negative reciprocal will only be valid when $p(x) \neq 0$ and $q(x) \neq 0$.
What if we’re working with whole numbers then? We begin by expressing the whole number as a fraction with $1$ as its denominator. Let’s say we have $m$ as the whole number, we start by expressing it as $\dfrac{m}{1}$ and follow the same process.

A similar process applies for functions such as $f(x)$ that are not rational functions.
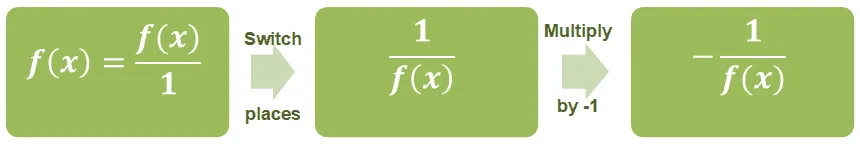
Take note that for the negative reciprocals to exist, both $m$ and $f(x)$ must not be equal to $0$.
Excited to try out problems involving negative reciprocals? First, let’s go ahead and summarize what we’ve learned so far about negative reciprocals.
Summary of reciprocal definition and properties
- This expression represents what occurs in finding the negative reciprocals: $ \boldsymbol{\dfrac{a}{b} \rightarrow – \dfrac{b}{a} }$.
- When given a whole number or a function that is not rational, begin by expressing the given as a fraction of 1.
- It is only possible for a constant or a function to have a negative reciprocal when both its numerator and denominator are not equal to $0$.
- A slope of a perpendicular line makes use of negative reciprocals.
That’s it. Make sure to keep these pointers in mind when solving the problems below.
Example 1
Complete the table below by finding the respective negative reciprocals of the following.
| Original Value | Negative Reciprocal |
| $\dfrac{1}{2}$ | |
| $-\dfrac{2}{3}$ | |
| $9$ | |
| $- 4\dfrac{1}{7}$ |
Solution
When finding the negative reciprocal, we begin by switching the fraction’s numerator and denominator places. Let’s work on the first two items first: $\dfrac{1}{2}$ and $-\dfrac{2}{3}$.
Hence, their reciprocals are $\dfrac{2}{1}$ and $-\dfrac{3}{2}$.
For each value, multiply $-1$ to find the corresponding negative reciprocal.
- $-1 \cdot \dfrac{2}{1} = -2$
- $-1 \cdot -\dfrac{3}{2}=\dfrac{3}{2}$.
We’ll actually apply the same process for the last two rows, but let’s first make sure we rewrite them in fraction form. The whole number $9$ can be written as $\dfrac{9}{1}$ and the mixed number $- 4\dfrac{1}{7}$ can be written as $-\dfrac{29}{7}$.
Once we have them in fraction forms, we can now switch the places of their corresponding numerators and denominators then multiplying the respective result by $-1$.
- $\begin{aligned}\dfrac{9}{1} \rightarrow \dfrac{1}{9} \rightarrow -\dfrac{1}{9} \end{aligned}$
- $\begin{aligned} -\dfrac{29}{7} \rightarrow \dfrac{-7}{29} \rightarrow \dfrac{7}{29} \end{aligned}$
Hence, we have the completed table as shown below.
| Original Value | Negative Reciprocal |
| $\dfrac{1}{2}$ | $-2$ |
| $-\dfrac{2}{3}$ | $\dfrac{3}{2}$ |
| $9$ | $-\dfrac{1}{9}$ |
| $- 4\dfrac{1}{7}$ | $-\dfrac{7}{29}$ |
Example 2
Let $h(x)$ be the negative reciprocal of $f(x)$ for each of the following functions. Find the $h(x)$. What are the restrictions for $x$ in each case?
a. $f(x) = \dfrac{1}{x – 1}$
b. $f(x) = \dfrac{2}{3(x +2)}$
c. $f(x) = x^2 – 3x – 54$
Solution
We apply the same process when finding the negative reciprocals of functions.
a. This means that we begin by switching the places of $1$ and $x – 1$ to find the reciprocal of $f(x)$. We then multiply the result by $-1$.
$\begin{aligned}h(x)&=-1\cdot \dfrac{x-1}{1}\\&=-1\cdot x – 1\\&\mathbf{-x + 1} \end{aligned}$
Since $h(x)$ is a linear expression, it has not restrictions. The function $f(x)$, however, must not have $x – 1 = 0$, so $\mathbf{x \neq 0}$.
b. We apply the same process from a. Hence, we have $h(x)$ as shown below.
$\begin{aligned}h(x)&=-1\cdot \dfrac{3(x+2)}{2}\\&=-1\cdot \dfrac{3x+6}{2}\\&=\mathbf{-\dfrac{3x+6}{2}} \end{aligned}$
The function $h(x)$ has a constant as its denominator, so it has no restrictions for $x$. The function $f(x)$, however, can’t have $3(x + 2) = 0$, so $\mathbf{x \neq -2}$.
c. Express $f(x)$ as a fraction by having $1$ as its denominator, so $f(x) = \dfrac{ x^2 – 3x – 54}{1}$. Now, apply the same process to find the negative reciprocal, $h(x)$.
$\begin{aligned}h(x)&=-1\cdot \dfrac{1}{x^2-3x-54}\\&=\mathbf{-\dfrac{1}{x^2-3x-54}}\\ \end{aligned}$
Since $f(x)$ is a polynomial, it has no restrictions for $x$. Its negative reciprocal, however, can’t have zero in its denominator. We can find the restrictions for $h(x)$ by finding the values where $ x^2 – 3x – 54$ is zero.
$ \begin{aligned} x^2 -3x – 54&=0\\(x – 9)(x + 6)&=0\\x&=9\\x&-6\end{aligned}$
This means that for $h(x)$ to be valid, $\mathbf{x \neq \{-6,9\}}$.
Example 3
The graph of the linear function, $f(x)$, is perpendicular to the graph of $h(x)$, which is also linear function. If $f(x)$ has a slope of $-\dfrac{2}{3}$, what is the slope of $h(x)$?
Solution
As we have mentioned in the discussion, finding negative reciprocals is crucial when finding the slopes of perpendicular lines.
Since we have the slope of $f(x)$, we can find the slope of $h(x)$ by finding the negative reciprocal of $-\dfrac{2}{3}$.
$\begin{aligned}m_\perp &= -1 \cdot-\dfrac{3}{2}\\&=\dfrac{3}{2} \end{aligned}$
This means that the slope of $h(x)$ is $\dfrac{3}{2}$ for it to be perpendicular to $f(x)$.
Example 4
The negative reciprocal of $f(x)$ is $\dfrac{x^2 – 2}{x – 5}$. What is the expression for $f(x)$?
Solution
This time, we’re given the negative reciprocal. We need to find the expression for $f(x)$ by reversing the steps:
- We start by multiplying $-1$ back on the negative reciprocal to reverse the changes in the sign.
- Switch the places of the negative reciprocal’s numerator and denominator.
$\begin{aligned}f(x)&=-1\cdot \dfrac{x-5}{x^2-2}\\&=\dfrac{-x+5}{x^2-2} \end{aligned}$
This means that $\mathbf{f(x) =\dfrac{-x+5}{x^2-2}}$.
Notice something about the steps? They are actually the same process because the negative reciprocal of a function’s negative reciprocal will be $\mathbf{f(x)}$.
Example 6
If a given number is twenty-seven times larger than its negative reciprocal’s square, find the number.
Solution
Let $n$ be the number we’re looking for, so its negative can be expressed as $-\dfrac{1}{n}$. Set up the equation representing the situation.
$n=27\cdot\left(-\dfrac{1}{n} \right )^2 $
Simplify this equation by multiplying both sides of the equation by $n^2$ and taking the cube root of both sides of the equation.
$\begin{aligned}n&=\dfrac{27}{n^2}\\n^3&=27\\\sqrt[3]{n^3} &=\sqrt[3]{27}\\n&=3 \end{aligned}$
This means that for the number to satisfy the condition, it must be equal to 3.
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
