Telescoping series – Components, Formula, and Technique

One of the most unique and interesting series we’ll learn in precalculus is the telescoping series. Telescoping series exhibit a unique behavior that will test our knowledge of algebraic manipulation, series, and partial sums.Telescoping series is a series that can be rewritten so that most (if not all) of the terms are canceled by a preceding or following term. This series has an extensive application in higher mathematics, computational theory and a fun series to explore while testing our algebraic skills. One of the most applied algebraic techniques in manipulating telescoping series is the use of partial fraction decomposition. Make sure to review and refresh your knowledge on this particular topic since we’ll be applying it extensively in this article.We’ll also be applying our knowledge on limits, so make sure to do a quick refresher on how we evaluate limits. Let’s begin by understanding the telescoping series’s components and eventually learn how the series got its name.

What is a telescoping series?

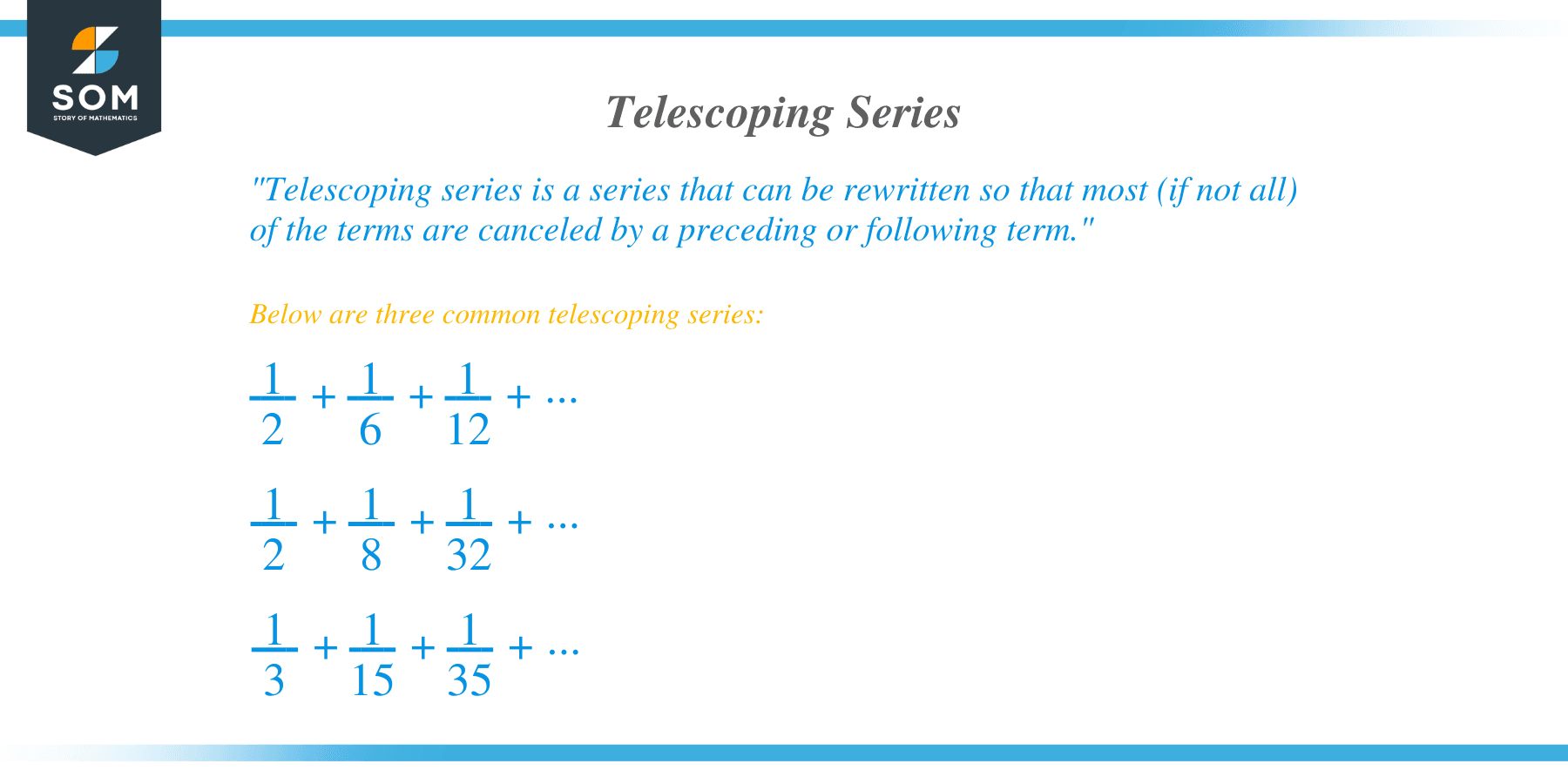
Identifying telescoping series can appear trickier than identifying simpler series such as arithmetic and geometric series. That’s because a telescoping series requires us to think creatively on how we can manipulate the terms to expand then simplify them later on.Below are three common telescoping series:

$\dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{12} + …$
$\dfrac{1}{2} + \dfrac{1}{8}+ \dfrac{1}{32} + …$
$\dfrac{1}{3} + \dfrac{1}{15} + \dfrac{1}{35} + …$

In the sections, we’ll learn how we can simplify series like these and why they’re each considered a telescoping series.

When we talk about telescoping series, it’s inevitable for us to talk about telescoping sums – this is the process of simplifying a series or an expression by expanding them first then canceling out the consecutive terms of the new expression.This is also why we call this technique telescoping sums and the series itself a telescoping series. Just like a telescope, for us to make sense of the value, we’ll need to expand the view first before we can focus on the values that matter.To better understand what the telescoping series is, let’s take a look at its algebraic form.

Telescoping series formula and definition

Let’s say we have $\sum_{n=1}^{\infty} b_n$, an infinite telescoping series, we can rewrite this as $b_n$ as $a_n – a_{n+1}$, where $a_n$ is a term from a properly constructed sequence.A series is said to be telescoping when we express it as $\sum_{n=1}^{\infty} b_n = \sum_{n=1}^{\infty} (a_n – a_{n+1})$\begin{aligned}\sum_{n=1}^{\infty} b_n &= (a_1 – a_2) + (a_2 – a_3) + (a_3 – a_4) + … + (a_{n-1} – a_n) \\&= a_1 + (-a_2 + a_2) + (-a_3 + a_3) + … + (-a_{n – 1} + a_{n – 1}) – a_n\\&= a_1 – a_n\end{aligned}When this happens, we simply cancel out the terms and retain the remaining values and we’ll have the most simplified form of the telescoping series as shown by the general form above.

How to find the sum of a telescoping series?

The best way to understand what makes a telescoping series unique is by simplifying the series and finding out its sum. Here are some helpful pointers when finding the sum of a telescoping series:

If it’s not yet given, find the expression for $a_n$ and $S_n$.
Use partial fraction decomposition to rewrite the rational expression as a sum of two simpler fractions.
Rewrite $a_n$ using as sum of these two fractions then find the value of $\lim_{n\rightarrow \infty} \sum_{n=1}^{\infty} S_n$.

Let’s take a look at one of the most common telescoping series we’ll probably encounter: $\sum_{n=1}^{\infty} \dfrac{1}{n(n + 1)}$.\begin{aligned}\sum_{n=1}^{\infty} \dfrac{1}{n(n + 1)} &= \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{12} + … + \dfrac{1}{n(n + 1)} \end{aligned}Finding the sum of this series may appear challenging at first, but with the steps we’ve mentioned, we’ll be able to find the sum of this telescoping series.We have the rational expression, $\dfrac{1}{n(n + 1)}$, we can rewrite this expression as $\dfrac{A}{n}$ and $\dfrac{B}{n + 1}$. Apply what we’ve learned in decomposing fractions to find $A$ and $B$.\begin{aligned}\dfrac{1}{n(n + 1)} &= \dfrac{A}{n} + \dfrac{B}{n + 1}\\1 &= A(n + 1) + B(n)\\0n + 1&= (A + B)n + A\\\\A+ B &= 0\\A&=1\\B&=-1\end{aligned}This means that we can rewrite $\dfrac{1}{n(n + 1)}$ as $\dfrac{1}{n} – \dfrac{1}{n + 1}$. Replace our rational expression with this decomposed form.\begin{aligned}\sum_{n=1}^{\infty} \dfrac{1}{n(n + 1)} &= \sum_{n=1}^{\infty} \left(\dfrac{1}{n} – \dfrac{1}{n + 1}\right) \\&= \left(1 -\dfrac{1}{2} \right) + \left(\dfrac{1}{2} – \dfrac{1}{3}\right) + \left(\dfrac{1}{3} – \dfrac{1}{4}\right) + … +\left(\dfrac{1}{n – 1} – \dfrac{1}{n}\right) + \left(\dfrac{1}{n} – \dfrac{1}{n + 1}\right) \end{aligned}We can rewrite this series by grouping the terms as shown below. \begin{aligned}\sum_{n=1}^{\infty} \dfrac{1}{n(n + 1)} &= 1 + \left(-\dfrac{1}{2} +\dfrac{1}{2} \right) + \left(-\dfrac{1}{3} +\dfrac{1}{3} \right) + … +\left(-\dfrac{1}{n – 1} + \dfrac{1}{n-1}\right) + \left(-\dfrac{1}{n} +\dfrac{1}{n}\right) – \dfrac{1}{n + 1}\\&=1 + \cancel{\left(-\dfrac{1}{2} +\dfrac{1}{2} \right)} + \cancel{\left(-\dfrac{1}{3} +\dfrac{1}{3} \right)} + … +\cancel{\left(-\dfrac{1}{n – 1} + \dfrac{1}{n-1}\right)} + \cancel{\left(-\dfrac{1}{n} +\dfrac{1}{n}\right)} – \dfrac{1}{n + 1}\\&= 1- \dfrac{1}{n +1} \end{aligned}Notice how the pairs now cancel each other and leaving the first and last terms behind? That’s the beauty of telescoping series. Now that we have a sum of $1 – \dfrac{1}{n + 1}$, we can simply find the limit of the sum as $n$ approaches infinity to find the \begin{aligned}\lim_{n \rightarrow \infty}\sum_{n=1}^{\infty} \dfrac{1}{n(n + 1)} &= \lim_{n \rightarrow \infty} \left(1 – \dfrac{1}{n +1}\right) \\&= 1 – 0\\&=0\end{aligned}Hence, the sum of the infinite telescoping series is $1$. More importantly, we’ve shown how we can apply partial fraction decomposition and limit laws to find the sum of an infinite telescoping series.Are you ready to try out more problems? Check out the sample problems we’ve provided for you.Example 1Find the sum of the telescoping series, $\sum_{n=1}^{\infty} \dfrac{1}{(2n – 1)(2n + 1)}$.SolutionWe already have the expression for $a_n = \dfrac{1}{(2n – 1)(2n + 1)}$, so we can proceed with rewriting $\dfrac{1}{(2n – 1)(2n + 1)}$ as a sum of two “simpler” fractions.\begin{aligned}\dfrac{1}{(2n – 1)(n + 1)} &= \dfrac{A}{2n – 1} + \dfrac{B}{2n + 1}\\ 1 &= A(2n + 1) + B (2n – 1)\\0n + 1 &= (2A + 2B)n + (A- B)\\\\2A + 2B &= 0\\ A – B &= 1\end{aligned}Since $A + B = 0$, we can substitute $A = -B$ into the second equation, $A – B = 1$.\begin{aligned}A – B &= 1\\ -B – B&= 1\\-2B &= 1\\B & = -\dfrac{1}{2}\end{aligned}This means that $A$ is equal to $\dfrac{1}{2}$. Let’s use these values to rewrite the original rational expression.\begin{aligned}\dfrac{1}{(2n – 1)(n + 1)} &= \dfrac{A}{2n – 1} + \dfrac{B}{2n + 1}\\&=\dfrac{\dfrac{1}{2}}{2n – 1} – \dfrac{\dfrac{1}{2}}{2n + 1}\\&= \dfrac{1}{4n – 2} -\dfrac{1}{4n + 2}\end{aligned}Using the new expression for $a_n$, we can expand the telescoping series as shown below.\begin{aligned}\sum_{n=1}^{\infty} \dfrac{1}{(2n – 1)(n + 1)} &=\sum_{n=1}^{\infty}\left( \dfrac{1}{4n – 2} -\dfrac{1}{4n + 2}\right)\\&= \left(\dfrac{1}{2} – \dfrac{1}{6} \right ) + \left(\dfrac{1}{6} – \dfrac{1}{10} \right ) + \left(\dfrac{1}{10} – \dfrac{1}{14} \right ) + … + \left[\dfrac{1}{4(n – 1) – 2} – \dfrac{1}{4(n – 1) + 2} \right ]+ \left(\dfrac{1}{4n – 2} – \dfrac{1}{4n + 2} \right )\end{aligned}Rearrange the terms and see how we can reduce the telescoping series into two terms.\begin{aligned}\sum_{n=1}^{\infty} \dfrac{1}{(2n – 1)(n + 1)} &= \dfrac{1}{2} + \cancel{\left( – \dfrac{1}{6} + \dfrac{1}{6} \right )}+ \cancel{\left( – \dfrac{1}{10} + \dfrac{1}{10} \right )} + \cancel{\left( – \dfrac{1}{14} + \dfrac{1}{14} \right )}+…+ \cancel{\left(-\dfrac{1}{4n – 2} + \dfrac{1}{4n – 2}\right)} – \dfrac{1}{4n + 2} \\&= \dfrac{1}{2} – \dfrac{1}{4n + 2}\end{aligned}We can now find the sum of the telescoping series by taking the limit of the $S_n =\dfrac{1}{2} – \dfrac{1}{4n + 2}$ as $n$ approaches $\infty$.\begin{aligned}S_n &=\dfrac{1}{2} – \dfrac{1}{4n + 2}\\\lim_{n \rightarrow \infty} S_n &= \lim_{n\rightarrow \infty} \left( \dfrac{1}{2} – \dfrac{1}{4n + 2}\right )\\&= \dfrac{1}{2}- 0\\&= \dfrac{1}{2}\end{aligned}This shows that the sum of $\sum_{n=1}^{\infty} \dfrac{1}{(2n – 1)(2n + 1)}$ is equal to $\dfrac{1}{2}$.Example 2Find the sum of the telescoping series, $\sum_{n=1}^{\infty} \dfrac{3}{n^2 + 4n + 3}$.SolutionWe can apply a similar process to rewrite $\dfrac{3}{n^2 + 4n + 3}$ as a sum of two simpler fractions.\begin{aligned}\dfrac{3}{n^2 + 4n + 3} &= \dfrac{3}{(n + 1)(n + 3)}\\&= \dfrac{A}{n + 3} + \dfrac{B}{n + 1}\\\\A(n + 3) + B(n + 1) &=3\\(A + B)n + (3A + B)&= 0n + 3\\A+B &=0\\3A+ B &= 3\end{aligned}Since $A + B = 0$, we can substitute $A = -B$ into the second equation, $3A + B = 3$.\begin{aligned}-3B + B &= 3\\ -2B &= 3\\B &= -\dfrac{3}{2}\end{aligned}Using $A = \dfrac{3}{2}$ and $B = -\dfrac{3}{2}$, we have $\sum_{n=1}^{\infty} \dfrac{3}{n^2 + 4n + 3} = \sum_{n=1}^{\infty} \left(\dfrac{3}{2(n + 1)} – \dfrac{3}{2(n + 3)}\right)$. Let’s use this to expand the telescoping series and reduce the series into fewer terms.\begin{aligned}\sum_{n=1}^{\infty} \left[\dfrac{3}{2(n + 1)} – \dfrac{3}{2(n + 1)}\right] &=\sum_{n=1}^{\infty} \left(\dfrac{3}{2(n + 1)}- \dfrac{3}{2(n + 3)}\right) \\&=\dfrac{3}{2}\sum_{n=1}^{\infty} \left[\dfrac{1}{(n + 1)}- \dfrac{1}{(n + 3)}\right]\\&=\dfrac{3}{2}\left[\left(\dfrac{1}{2} – \dfrac{1}{4} \right ) + \left(\dfrac{1}{3} – \dfrac{1}{5} \right )+ \left(\dfrac{1}{4} – \dfrac{1}{6} \right )+ \left(\dfrac{1}{5} – \dfrac{1}{7} \right ) + …+ \left(\dfrac{1}{n} – \dfrac{1}{n+2} \right )+ \left(\dfrac{1}{n+1} – \dfrac{1}{n+3} \right )\right ]\end{aligned}Group the terms with odd denominators and those with even denominators. Cancel the terms out whenever possible, then simplified the expression in terms of $n$.\begin{aligned}\sum_{n=1}^{\infty} \left[\dfrac{3}{2(n + 1)} – \dfrac{3}{2(n + 1)}\right] &= \dfrac{3}{2}\left[\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6} + …- \dfrac{1}{n} + \dfrac{1}{n}-\dfrac{1}{n +2}\right ) \right ]\\&\phantom{xxx} +\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{8} + …- \dfrac{1}{n+1} + \dfrac{1}{n+1}-\dfrac{1}{n +3}\right )\\&=\dfrac{3}{2}\left[\left(\dfrac{1}{2} – \dfrac{1}{n + 2} \right ) + \left(\dfrac{1}{3} – \dfrac{1}{n + 3} \right )\right] \end{aligned}We can now find the sum of the telescoping series by evaluating the limit of the sum’s simplified expression when $n$ approaches infinity.\begin{aligned}\sum_{n=1}^{\infty} \dfrac{3}{n^2 + 4n + 3} &= \lim_{n \rightarrow \infty}\dfrac{3}{2}\left[\left(\dfrac{1}{2} – \dfrac{1}{n + 2} \right ) + \left(\dfrac{1}{3} – \dfrac{1}{n + 3} \right )\right]\\&=\dfrac{3}{2}\lim_{n \rightarrow \infty}\left[\left(\dfrac{1}{2} – \dfrac{1}{n + 2} \right ) + \left(\dfrac{1}{3} – \dfrac{1}{n + 3} \right )\right] \\&= \dfrac{3}{2}\left[\left(\dfrac{1}{2} – 0\right)+ \left(\dfrac{1}{3} – 0\right)\right]\\&=\dfrac{3}{2}\left(\dfrac{1}{2} + \dfrac{1}{3}\right)\\&=\dfrac{3}{2} \cdot \dfrac{5}{6}\\&= \dfrac{5}{4}\end{aligned}From this, we can see that $\sum_{n=1}^{\infty} \dfrac{3}{n^2 + 4n + 3}$ is equal to $\dfrac{5}{4}$ or $1.15$.These are two great examples of how we can find the sum of a telescoping series. They show how knowing how to manipulate expressions is crucial in simplifying and evaluating these series.Try out the problems shown below if you want to work on more telescoping series.

Telescoping series – Components, Formula, and Technique

What is a telescoping series?

Telescoping series formula and definition

How to find the sum of a telescoping series?

Practice Questions

Previous Lesson | Main Page | Next Lesson