- Home
- >
- Parametrize a line – Equations, Graphs, and Examples
JUMP TO TOPIC
Parametrize a line – Equations, Graphs, and Examples
 We can parametrize lines and line segments to understand the initial and ending positions of objects that we are observing. Learning about the steps of parametrizing a line can help describe the motion of an object or the behavior of the object given the third parameter.
We can parametrize lines and line segments to understand the initial and ending positions of objects that we are observing. Learning about the steps of parametrizing a line can help describe the motion of an object or the behavior of the object given the third parameter.
We can parametrize a line by rewriting the values of $\boldsymbol{x}$ and $\boldsymbol{y}$ in terms of a third parameter but still satisfy the original equation.
This topic will be most helpful when you’ve already been introduced to the idea behind parametric equations and, of course, the equation of a line.
In this article, we’ll focus on rewriting equations of lines in parametric forms, learn how to graph lines from parametric equations, and explore problems that involve parametrizing linear equations.
How to parametrize a line?
It’s important to remember that any function can be expressed as a parametric curve. Let’s say we have $y = f(x)$, we can find a way to express $x$ and $y$ in terms of another parameter, $t$.
When parametrizing linear equations, we can begin by letting $x = f(t)$ and rewrite $y$ wit h this parametrization: $y = g(t)$. Remember that the standard form of a linear equation is $y = mx + b$, so if we parametrize $x$ to be equal to $t$, we’ll have the following resulting parametric forms:
\begin{aligned} x&= f(t)\\y &= g(t)\\\\x &= t\\y&= mt + b\end{aligned}
Let’s say we have $y = -3x + 5$, if we want to paramaterize this equation, we simply let $x $ be $t$ and rewrite $y$ accordingly as shown below.
\begin{aligned}x &= t\\y&= -3t + 5\end{aligned}
This set of equations looks just like the original forms, so why do we need to parametrize the equations? That’s because there are instance where we want to find the position, $(x, y)$, of the data or object we’re observing at a given value of $t$.
Let’s say the equation $y = -3x + 5$ models the vertical position of an object given its horizontal position. If we want to know the object’s vertical and horizontal coordinates at the time, $t$, parametric, this equation will come in handy.
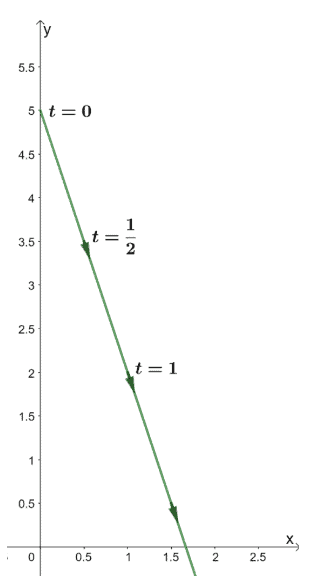
Here’s the actual graph of the parametric equations, $\left\{\begin{matrix}x=t\phantom{xxxxx}\\ y= -3t + 5\end{matrix}\right.$, so as you can see, by parametrizing the rectangular equation, we have a better understanding of the object’s positions at different values of $t$.
There are instances where we’ll have to use a different expression for $x$, affecting the expression for $y$ and the graph of the parametric line. For example, if we have $x = 2t$ instead, we’ll have the following parametric equations.
\begin{aligned}x &= 2t\\y&= -3(2t) + 5\\y&= -6t + 5\end{aligned}
The graph of these parametric equations will be much steeper and will be progressing faster.
When two points are given to represent the parametric line, make sure to change the rate of change between the two coordinates of $x$ and $y$. We can then express the parametric equations in terms of $x(t) = m_1t + b_1$ and $y(t) = m_2t + b_2$.
Graphing parametric equations of a line
We’ve shown you an example of a graph representing a set of parametric equations. In this section, we’ll learn how to graph parametric equations that represent a line. As with graphing parametric equations, in general, we can use the following pointers as a guide:
- Make sure that the linear equation is in its point-slope form.
- Assign key values for $t$. For example, if the slope of the equation is $\dfrac{1}{3}$, it will be helpful to use values of $t$ that are multiples of $3$.
- Find the values of $x$ and $y$ using the assigned values for $t$.
- Plot these points and graph the line. Make sure to take note of the direction.
For example, if we want to graph the parametric equations, $\left\{\begin{matrix}x=t\phantom{xxxxx}\\ y= \dfrac{1}{2}t + 2\end{matrix}\right.$, we can begin by assigning key values for $t$. (First step was skipped since $y$ is already in point-slope form)
$\boldsymbol{t}$ | $\boldsymbol{x = t}$ | $\boldsymbol{y = \dfrac{1}{2}t + 2}$ | $\boldsymbol{(x, y)}$ |
$0$ | \begin{aligned}x &= 0\end{aligned} | \begin{aligned}y &= \dfrac{1}{2}(0) + 2\\&= 2\end{aligned} | \begin{aligned}(0, 2)\end{aligned} |
$2$ | \begin{aligned}x &= 2\end{aligned} | \begin{aligned}y &= \dfrac{1}{2}(2) + 2\\&= 3\end{aligned} | \begin{aligned}(2, 3)\end{aligned} |
$4$ | \begin{aligned}x &= 4\end{aligned} | \begin{aligned}y &= \dfrac{1}{2}(4) + 2\\&= 4\end{aligned} | \begin{aligned}(4, 4)\end{aligned} |
$6$ | \begin{aligned}x &= 6\end{aligned} | \begin{aligned}y &= \dfrac{1}{2}(6) + 2\\&= 5\end{aligned} | \begin{aligned}(6, 5)\end{aligned} |
$8$ | \begin{aligned}x &= 8\end{aligned} | \begin{aligned}y &= \dfrac{1}{2}(8) + 2\\&= 6\end{aligned} | \begin{aligned}(8, 6)\end{aligned} |
Let’s go ahead and plot these coordinates and include the values of $t$. Connect these coordinates to graph the parametric curve (or line for our case).
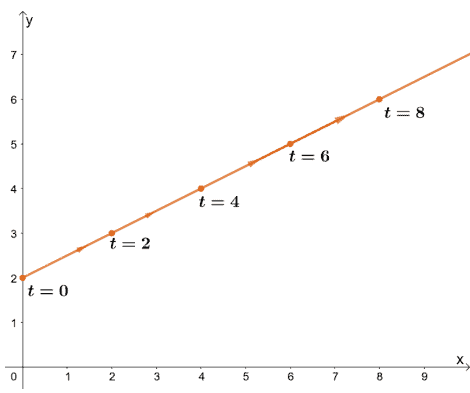
The parametric equations graph shows the direction and tells us how the graph progresses as the value of $t$ increases.
We can apply a similar process when parametrizing equations with a given interval for $t$. Make sure to keep in mind if the direction of the segment is given.
These are all the general concepts that you need to learn when parametrizing a line. In the next section, we’ll explore more examples to help you master this topic.
Example 1
Parametrize the equation the following equations:
a. $y = -3x + 5$
b. $2y = 6x – 8$
c. $-6x + 4y = 96$
Solution
When parametrizing a linear equation, we begin by assuming $x = t$, then use this parametrization to express $y$ in terms of $t$.
\begin{aligned}x = t\\y &= -3t + 5\end{aligned}
For the second item, let’s divide both sides of the equation by $2$ first.
\begin{aligned}2y &= 6x – 8\\ y&= 3x -4\end{aligned}
Once we have the simplified equation, we can now substitute $x = t$ to parametrize the linear equation.
\begin{aligned}x = t\\y &= 3t – 4\end{aligned}
For the third equation, let’s rewrite $-6x + 4y = 96$ in its point-slope form, as shown below.
\begin{aligned}-6x + 4y &= 96\\4y &= 6x + 96\\y &= \dfrac{3}{2}x + 24\end{aligned}
Now that the equation is in its point-slope form, we can now substitute $x = t$.
\begin{aligned}x = t\\y &= \dfrac{3}{2}t +24\end{aligned}
Example 2
Parametrize the equation, $y = 2x + 1$, in terms of $-2 \leq t\leq 2$. Graph the resulting line segment if the segment’s direction is moving from right to left.
Solution
The equation, $y = 2x + 1$, is already in point-slope form, so we can go ahead and substitute $x = t$ to parametrize the equation.
\begin{aligned}x = t\\y &= 2t +1\end{aligned}
With the parametric equation, we can assign values of $t$ between $-2$ and $2$.
$\boldsymbol{t}$ | $\boldsymbol{x = t}$ | $\boldsymbol{y = 2t + 1}$ | $\boldsymbol{(x, y)}$ |
$-2$ | \begin{aligned}x &= -2\end{aligned} | \begin{aligned}y &= 2(-2) + 1\\&= -3\end{aligned} | \begin{aligned}(-2, -3)\end{aligned} |
$0$ | \begin{aligned}x &= 0\end{aligned} | \begin{aligned}y &= 2(0) + 1\\&=1\end{aligned} | \begin{aligned}(0, 1)\end{aligned} |
$2$ | \begin{aligned}x &= 2\end{aligned} | \begin{aligned}y &= 2(2) + 1\\&= 5\end{aligned} | \begin{aligned}(2, 5)\end{aligned} |
Since the line segment is expected to progress from right to left, we begin plotting the coordinates of $t = 2 \rightarrow t = 0 \rightarrow t = -2$.
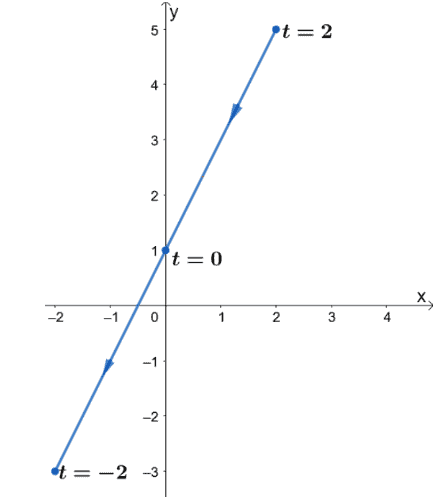
This graph shows how the direction may vary depending on what’s given. Be careful with problems like and double-check if you’re asked to graph a parametric line from left to right or right to left.
Example 3
An object travels at a constant rate along a straight path from $(-8, 2)$ to $(4,-4)$ in six seconds. The coordinates are measured in meters. Find parametric equations that represent the position of the object.
Solution
This problem is an application of parametrizing linear equations. However, this time, we can see that the object moves from $(-8, 2)$ to $(4,-4)$ in just six seconds.
We can’t assume that the parametric equation of $x$ is $t$, so let’s assume that both $x$ and $y$ are of the form $y = mt + b$. The value of $m$ for $x$ and $y$ will depend on the change in $x$ and $y$, respectively, within $6$ seconds.
Since we have the starting values for $x$ and $y$ ($x = -8$ and $y = 2$), we can use this to act as $b$. Once we have the values of the $m$ and $b$ for each parametric equation, we can now express $x(t)$ and $y(t)$ as $m_1 t + b_1$ and $m_2 t + b_2$, respectively.
Parametric Equation | $\boldsymbol{m}$ | $\boldsymbol{b}$ | $\boldsymbol{mt + b}$ |
$x(t)$ | $\dfrac{-8 – 4}{6} = -2$ | $-8$ | $x(t) = -2t – 8$ |
$y(t)$ | $\dfrac{2 – -4}{6} = 1$ | $2$ | $y(t) = t + 2$ |
This means that the parametrized equations representing the position of the object are $\left\{\begin{matrix}x=-2t -8\\ y= t + 2\phantom{xxx}\end{matrix}\right.$.
This shows that there are instances where both $x(t)$ and $y(t)$ will be in point-slope forms, so be careful in assuming right away that $x = t$ is the parametrized equation for $x$.
Practice Question
![]()
Open Problem
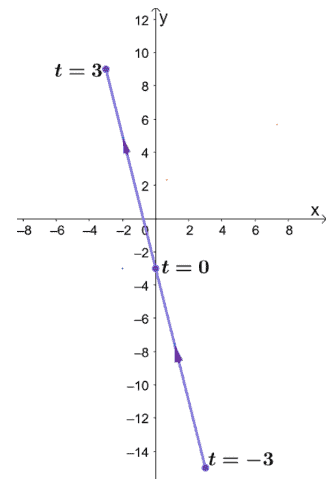
Use your answer from Problem Question 4 to parametrize the equation, $y = -4x – 3$, in terms of $-3 \leq t\leq 3$.
Graph the resulting line segment if the segment’s direction is moving from right to left.
Open Problem Solution
Images/mathematical drawings are created with GeoGebra.
