Divergent series math- Definition, Divergence Test, and Examples

A divergent series is an important group of series that we study in our precalculus and even calculus classes. In algorithms and computations where we need accuracy is an essential component; knowing whether a given series is divergent or not can help us return the best result.

The divergent series is a type of series that contains terms that do not approach zero. This means that the sum of this series approaches infinity.

The creativity needed to manipulate divergent (and convergent) series has inspired contemporary mathematicians. It will also help us learn about divergent series to appreciate our knowledge of algebraic manipulation and evaluating limits.

In this article, we’ll learn about the special components of divergent series, what makes a series divergent, and predict the sum of a given divergent series. With these core topics, make sure to refresh your knowledge on:

• Evaluating limits, especially when the given variable approaches $\infty$.

• The common infinite series and sequences including the arithmetic, geometric, alternating, and harmonic series.

• Knowing why the nth term test is important for divergent series.

Let’s go ahead and begin by visualizing how a divergent series behaves and understand what makes this series unique.

What is a divergent series?                

The most fundamental idea of a divergent series is that the values of the term increase as we progress with the terms’ order.

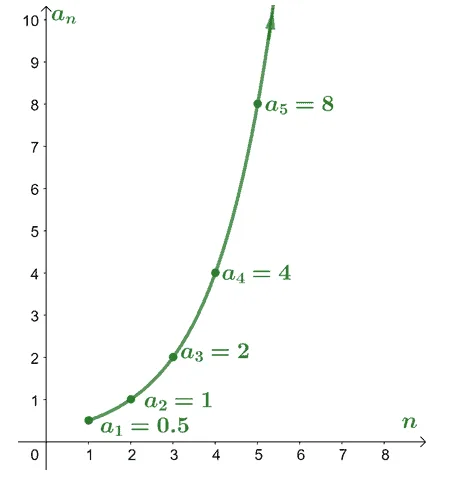
Here’s how the first five terms of the divergent series, $\sum_{n=1}^{\infty} \dfrac{1}{2} (2^{n-1})$, would appear when we plot $a_n$ with respect to $n$. This shows that as we progress through the series, the value of the terms does not approach a fixed value. Instead, the values are expanding and are approaching infinity.

This is a great visualization of how the terms of a given divergent series approach infinity. Another possible result for a divergent series’ sum is a sum that goes up and down.

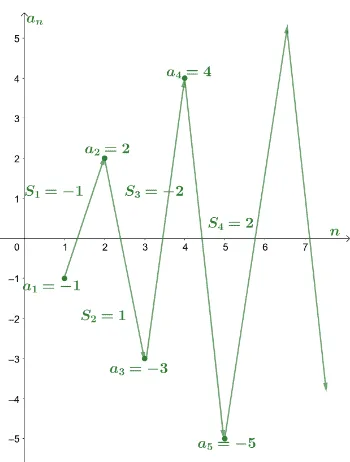
Here’s an example of a divergent series where its partial sums’ values go up and down. Many alternating series examples are divergent as well, so knowing how they behave is essential.

Now that we understand the concept behind divergence, why don’t we define what makes a divergent series unique through limits?

Divergent series definition

A divergent series is a series that contain terms in which their partial sum, $S_n$, does not approach a certain limit.

Let’s go back to our example, $\sum_{n=1}^{\infty} \dfrac{1}{2} (2^{n-1})$, and observe how $a_n$ behaves as it approaches infinity.

\begin{aligned}\sum_{n=1}^{\infty} \dfrac{1}{2} (2^{n-1}) &= \dfrac{1}{2} + 1 + 2+ 4 + 8 + …\end{aligned}

From this, we can see that as we add in more terms, the partial sum blows up and will not approach any value. This behavior is what makes a divergent series unique and is the basis of its definition.

How to tell if a series is divergent?              

Now that we understand what makes a series divergent let’s focus on understanding how we can identify divergent series given their terms and summation forms.

Let’s say we’re given a series in summation form, $\sum_{n=1}^{\infty} a_n$, we can determine whether it is divergent or not using the nth term test.

We can tell if the series is divergent by taking the limit of $a_n$ as $n$ approaches infinity. When the result is not equal to zero or does not exist, the series diverges.

\begin{aligned}\sum_{n=1}^{\infty} a_n\\\lim_{n \rightarrow \infty} a_n &\neq 0\\\lim_{n \rightarrow \infty} a_n &= \text{DNE} \\\Rightarrow \boldsymbol{\text{Divergent}}\end{aligned}

What if we’re given the terms of the series? Make sure to express the series in terms of $n$, then perform the nth term test.

For example, if we want to test $2 + 4 + 6 + 8 + 10 + …$ for divergence, we’ll have to express this first in summation form by first observing how each term progresses.

\begin{aligned}2 &= 2(1)\\4&= 2(2)\\ 6 &= 2(3) \\8 &= 2(4)\\.\\.\\.\\a_n &= 2n\end{aligned}

This means that the series is equivalent to $\sum_{n=1}^{\infty} 2n$. We can now apply the nth term test by taking the limit of $a_n$.

\begin{aligned}\lim_{n \rightarrow \infty} a_n &= \lim_{n \rightarrow \infty} 2n\\&= \infty\\&\neq 0 \end{aligned}

This shows that the series is indeed divergent. Also, we can intuitively determine how the partial sums behave, and we can see that for our example, the partial sums will continue to increase as more terms are accounted for.

Now that we know the important components and conditions of the divergent series let’s familiarize ourselves with the process by answering the problems shown below.

Example 1

Let’s say we have the series, $S_n = 3 + 6 + 9 + 12 + …$, find the next two terms of this series. Make sure to answer the follow-up questions shown below.

    a. Complete the table shown below.

    b. What can you say about the series based on its partial sums?
    c. Express the series in summation form.

    d. Use the expression from 1c to confirm whether the series is divergent or not.

Solution

We can see that to find the next term, and we’ll need to add $3$ on the previous term. This means that the next two terms are $12 + 3= 15$ and $15 + 3 =18$.

Using these terms, let’s observe how their partial sums behave.

From this, we can see that as we add more terms, the partial sums will continue to increase. This tells us that the series may be divergent.

In terms of $n$, we can see that to find the $n$th term; we multiply $n$ by $3$.

\begin{aligned}3&= 3(1)\\6&= 3(2)\\9 &= 3(3)\\ 12&=3(4)\\.\\.\\.\\ a_n &= 3n\end{aligned}

Hence, in summation form, the series is equal to $\sum_{n=1}^{\infty} 3n$.

Let’s observe what happens if we take the limit of $a_n$ as $n$ approaches infinity.

\begin{aligned}\lim_{n \rightarrow \infty} a_n &= \lim_{n \rightarrow \infty} 3n \\&= \infty \\&\neq 0\end{aligned}

Since $\lim_{n \rightarrow \infty} a_n \neq 0$, we can confirm that the series is indeed divergent.

Example 2

Rewrite the following series in summation notation, then determine whether the given series is divergent.

a. $-3+ 6 -9 + 12- …$

b. $\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{9} + …$

c. $\dfrac{2}{6} + \dfrac{3}{7}+ \dfrac{4}{8} + \dfrac{5}{9}…$

d. $\dfrac{1}{2} + \dfrac{4}{5} + \dfrac{9}{10} + …$

Solution

Let’s observe the first few terms of the first series we’re working on. Once we see a pattern, we can then find an expression of the $n$th term.

\begin{aligned}-3 &= (-1)^1(3\cdot 1)\\6 &= (-1)^2(3\cdot 2)\\-9 &= (-1)^3(3\cdot 3)\\12 &= (-1)^4(3\cdot 4)\\.\\.\\.\\a_n &= (-1)^n(3n)\end{aligned}

This means that $-3+ 6 -9 + 12- … = \sum_{n=1}^{\infty} (-1)^n(3n)$ .

Now that we have the expression for $a_n$, we can test the series for divergence by taking the limit of $a_n$ as $n$ approaches infinity.

\begin{aligned}\lim_{n\rightarrow \infty} a_n &= \lim_{n\rightarrow \infty} (-1)^{n} 3n \\ &= \text{DNE}\\ &\neq 0\end{aligned}

Since the limit does not exist for this series (that makes sense since the values would go up and down for alternating series), the series is divergent.

We’ll apply a similar approach for the next series: observe the first few terms to find $a_n$.

\begin{aligned}\dfrac{1}{3} &= \dfrac{1}{3 \cdot 1}\\\dfrac{1}{6} &= \dfrac{1}{3\cdot 2}\\\dfrac{1}{9} &= \dfrac{1}{3\cdot 3} \\.\\.\\.\\a_n &= \dfrac{1}{3n}\end{aligned}

From this, we can see that the series is equivalent to $\sum_{n=1}^{\infty} \dfrac{1}{3n}$ and consequently, $a_n = \dfrac{1}{3n}$. Let’s go ahead and find the limit of $a_n$ as $n$ approaches infinity to see if the series is divergent.

\begin{aligned}\lim_{n\rightarrow \infty} a_n &= \lim_{n\rightarrow \infty} \dfrac{1}{3n} \\&= 0\end{aligned}

Since the value of $\lim_{n\rightarrow \infty} a_n = 0$ , the series is not divergent. We may use other tests to see if the series is convergent, but that’s beyond this article’s scope. In case you’re interested, check out the article we wrote about the different tests for convergence.

Moving on to the third series, we’ll once again observe the first four terms. This may be a bit tricky since both the numerator and denominator change for each term.

\begin{aligned}\dfrac{2}{6} &= \dfrac{1+1}{1+5}\\\dfrac{3}{7} &= \dfrac{2+1}{2+5}\\\dfrac{4}{8} &= \dfrac{3+1}{3+5}\\\dfrac{5}{9} &= \dfrac{4+1}{4+5}\\.\\.\\.\\a_n &= \dfrac{n + 1}{n + 5}\end{aligned}

This means that the summation form of the series is equivalent to $\sum_{n=1}^{\infty} \dfrac{n + 1}{n + 5}$. We can use $a_n = \dfrac{n + 1}{n + 5}$ to determine whether the series is divergent or not.

\begin{aligned}\lim_{n\rightarrow \infty} a_n &=\lim_{n\rightarrow \infty} \dfrac{n +1}{n +5} \\&=\lim_{n\rightarrow \infty}\dfrac{n +1}{n +5} \cdot \dfrac{\dfrac{1}{n}}{\dfrac{1}{n}}\\&=\lim_{n\rightarrow \infty} \dfrac{1 + \dfrac{1}{n}}{1 + \dfrac{5}{n}}\\&= \dfrac{1+0}{1+0}\\&= 1\\&\neq 0 \end{aligned}

Since $\lim_{n\rightarrow \infty} a_n \neq 0$, we can see confirm that the series is divergent.

Want to work on a more challenging series? Let’s try the fourth one and find the expression for $a_n$.

\begin{aligned}\dfrac{1}{2} &= \dfrac{1^2}{1^2+1}\\\dfrac{4}{5} &= \dfrac{2^2}{2^2 +1}\\\dfrac{9}{10} &= \dfrac{3^2}{3^2 +1}\\.\\.\\.\\a_n &= \dfrac{n^2}{n^2 + 1}\end{aligned}

This means that in summation notation, the fourth series is equal to $\sum_{n=1}^{\infty} \dfrac{n^2}{n^2 + 1}$. Now that we have the expression for $a_n$, we can evaluate $\lim_{n\rightarrow \infty} a_n$ to check if the series is divergent or not.

\begin{aligned}\lim_{n\rightarrow \infty} a_n &=\lim_{n\rightarrow \infty} \dfrac{n^2}{n^2 + 1} \\&=\lim_{n\rightarrow \infty}\dfrac{n^2}{n^2 + 1} \cdot \dfrac{\dfrac{1}{n^2}}{\dfrac{1}{n^2}}\\&=\lim_{n\rightarrow \infty} \dfrac{1}{1 + \dfrac{1}{n^2}}\\&= \dfrac{1}{1 + 0}\\&= 1\\&\neq 0 \end{aligned}

Since the limit of $a_n$ as $n$ approaches infinity, the series is indeed divergent.

Example 3

Show that the series, $\sum_{n=1}^{\infty} \dfrac{14 + 9n + n^2}{1 + 2n + n^2}$, is divergent.

Solution

We are given the summation form of the series already, so we can apply the nth term test to confirm the divergence of the series. As a refresher, when we have $\sum_{n=1}^{\infty} a_n$, we can check the series’ divergence by finding $\lim_{n\rightarrow \infty} a_n$.

\begin{aligned}\lim_{n\rightarrow \infty} a_n &=\lim_{n\rightarrow \infty} \dfrac{14 + 9n + n^2}{1 + 2n + n^2}\\&=\lim_{n\rightarrow \infty}\dfrac{14 + 9n + n^2}{1 + 2n + n^2} \cdot \dfrac{\dfrac{1}{n^2}}{\dfrac{1}{n^2}}\\&=\lim_{n\rightarrow \infty} \dfrac{\dfrac{14}{n^2} + \dfrac{9}{n} + 1}{\dfrac{1}{n^2} + \dfrac{2}{n} + 1}\\&= \dfrac{0 + 0+ 1}{0 + 0 + 1}\\&= 1\\&\neq 0 \end{aligned}

When the limit of $a_n$ does not exist or is not equal to $0$, the series will be divergent. From our result, we can see that $\lim_{n\rightarrow \infty} \neq 0$, so the series is divergent.