JUMP TO TOPIC
Orthogonal Vector – Explanation and Examples
In the realm of vector geometry, we have covered almost every concept of vectors. We covered normal vectors, vector equations, vector dot products, and many others. But one of the most important concepts in this domain is the understanding of an orthogonal vector.
Orthogonal vectors are defined as:
“2 vectors are called orthogonal if they are perpendicular to each other, and after performing the dot product analysis, the product they yield is zero.”
In this topic, we will focus on the following areas:
- What is an orthogonal vector?
- How to find the orthogonal vector?
- What are the properties of an orthogonal vector?
- Examples
- Practice problems
What Is An Orthogonal Vector?
In mathematical terms, the word orthogonal means directed at an angle of 90°. Two vectors u,v are orthogonal if they are perpendicular, i.e., they form a right angle, or if the dot product they yield is zero.
So we can say,
u⊥v or u·v=0
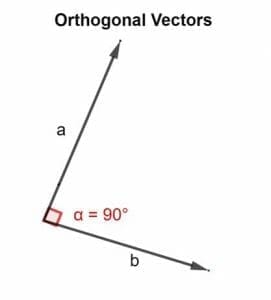
Hence, the dot product is used to validate whether the two vectors which are inclined next to each other are directed at an angle of 90° or not.
If we dive into the orthogonal vector properties, we get to know that the zero vector, which is basically a zero, is practically orthogonal to every vector. We can validate this because u.0=0 for any vector u, the zero vector is orthogonal to every vector. This is because the zero vector is zero and will obviously produce a null or a zero result upon being multiplied by any number or any vector.
Two vectors, u and y, in an inner product space, V, are orthogonal if their inner product is zero
(u,y)=0
Now that we know that the dot product is the major key for finding out whether the 2 vectors are orthogonal or not let’s conduct some examples for better understanding.
Example 1
Check whether the vectors a = i + 2j and b = 2i – j are orthogonal or not.
Solution
For checking whether the 2 vectors are orthogonal or not, we will be calculating the dot product of these vectors:
a.b = (1 · 2) + (2 · (-1))
a.b = 2 – 2
a.b = 0
Hence as the dot product is 0, so the two vectors are orthogonal.
Example 2
Are the vectors a = (3, 2) and b = (7, -5} orthogonal?
Solution
For checking whether the 2 vectors are orthogonal or not, we will be calculating the dot product of these vectors:
a.b = (3.7) + (7. (-5))
a.b = 21 – 35
a.b = -14
Since the dot product of these 2 vectors is not a zero, these vectors are not orthogonal.
How To Find An Orthogonal Vector?
We have already discussed that one way of finding the orthogonal vectors is by checking their dot product. If the dot product yields a zero answer, it is evident that the vectors being multiplied were actually orthogonal or perpendicular.
The general which can be used in this regard is as follows:
a.b = 0
This concept can be extended in the form of vector components as well.
The general equation, in this case, becomes something like the following:
a.b = (ax.bx) + (ay.by)
a.b = 0
Hence, the vectors’ major requirement to be orthogonal is that they should always deliver a dot product that gives us the zero result.
But let’s consider some other scenarios and methodologies as well.
The 2 vectors being multiplied can exist in any plane. There is no restriction for them to be limited to the two-dimensional planes only. So, let’s extend our study to three-dimensional planes as well.
Orthogonal Vector In Case Of Two-Dimensional Plane
Most of the problems in mathematics are restricted to two-dimensional planes. Such a plane exists of only 2 axes, namely the x and the y-axis. In the section of unit vectors, we have also discussed that these axes can be represented in terms of unit vectors as well; the x-axis in the form of the unit vector i and the y-axis in the form of the unit vector j.
Now, let’s consider that there are 2 vectors, named a and b, which exist in a two-dimensional plane. We have to testify whether these two vectors are orthogonal to each other or not, in other terms being perpendicular to one another.
We have concluded that to check for the orthogonality, we evaluate the dot product of the vectors existing in the plane. So, the dot product of the vectors a and b would be something as shown below:
a.b = |a| x |b| x cosθ
If the 2 vectors are orthogonal or perpendicular, then the angle θ between them would be 90°.
As we know,
cosθ = cos 90°
And,
cos 90° = 0
So, we can rewrite the dot product equation as:
a.b = |a| x |b| x cos 90°
a.b = 0
We can also express this phenomenon in terms of vector components.
a.b = ax.bx + ay.by
And we mentioned above that in terms of representation on the basis of unit vectors; we can use the characters i and j.
Hence,
a.b = ai.bi + aj.bj
a.b = 0
Therefore, if the dot product also yields a zero in the components multiplication case, then the 2 vectors are orthogonal.
Example 3
Find whether the vectors a = (5, 4) and b = (8, -10) are orthogonal to one another or not.
Solution
For checking whether the 2 vectors are orthogonal or not, we will be calculating the dot product of these vectors:
a.b = ai.bi + aj.bj
a.b = (5.8) + (4. -10)
a.b = 40 – 40
a.b = 0
Hence, it is proved that the two vectors are orthogonal in nature.
Example 4
Find whether the vectors a = (2, 8) and b = (12, -3) are orthogonal to one another or not.
Solution:
For checking whether the 2 vectors are orthogonal or not, we will be calculating the dot product of these vectors:
a.b = ai.bi + aj.bj
a.b = (2.12) + (8. -3)
a.b = 24 – 24
a.b = 0
Hence, it is proved that the two vectors are orthogonal in nature.
Orthogonal Vector In Case Of Three-Dimensional Plane
Most of the real-life problems require the vectors to exits in a three-dimensional plane. When we talk about three-dimensional planes, we are accompanied by another axis, namely the z-axis.
In this case, with the inclusion of the third axis, the z-axis will consist of 3 components, each directed along its respective axis if we say that any vector exists in a three-dimensional plane. In such a case, the 3 components of a vector in a three-dimensional plane would be the x-component, the y-component, and the z-component.
If we represent these components in terms of unit vectors, then we already know that for the x and y-axis, we use the characters i and j to represent their components. But now that we have a third axis and simultaneously the third component, we need an additional third representation.
So, for this third axis, we use the character k for the representation of the unit vector along the z-axis.
Now, consider that 2 vectors exist in a three-dimensional plane. These vectors would obviously have 3 components, and the dot product of such vectors can be found below:
a.b = ax.bx + ay.by + az.bz
Or, in the terms of unit vectors i, j, and k:
a.b = ai.bi + aj.bj + ak.bk
a.b = 0
Hence, if this result yields a dot product of 0, we will then be able to conclude that the 2 vectors in a three-dimensional plane are perpendicular or orthogonal in nature.
Example 5
Check whether the vectors a = (2, 3, 1) and b = (3, 1, -9) are orthogonal or not.
Solution
To check whether these 2 vectors are orthogonal or not, we will be calculating their dot product. Since these 2 vectors have 3 components, hence they exist in a three-dimensional plane.
So, we can write:
a.b = ai.bi + aj.bj + ak.bk
Now, putting the values in the formula:
a.b = (2.3) + (3.1) + (1. -9)
a.b = 6 + 3 -9
a.b = 0
As the dot product is zero, hence these 2 vectors in a three-dimensional plane are orthogonal in nature.
Example 6
Find whether the 2 vectors a = i + 2j and b = 2i -j + 10k are orthogonal or not.
Solution
To check whether these 2 vectors are orthogonal or not, we will be calculating their dot product. Since these 2 vectors have 3 components, hence they exist in a three-dimensional plane.
So, we can write:
a.b = ai.bi + aj.bj + ak.bk
Now, putting the values in the formula:
a.b = (1.2) + (2. -1) + (0.10)
a.b = 2 -2 + 0
a.b = 0
As the dot product is zero, hence these 2 vectors in a three-dimensional plane are orthogonal in nature.
Example 7
Check whether the 2 vectors a = (2, 4, 1) and b = (2, 1, -8) are orthogonal.
Solution
To check whether these 2 vectors are orthogonal or not, we will be calculating their dot product. Since these 2 vectors have 3 components, hence they exist in a three-dimensional plane.
So, we can write:
a.b = ai.bi + aj.bj + ak.bk
Now, putting the values in the formula:
a.b = (2.2) + (4.1) + (1. -8)
a.b = 4 + 4 – 8
a.b = 0
As the dot product is zero, hence these 2 vectors in a three-dimensional plane are orthogonal in nature.
Properties Of The Orthogonal Vectors
Now that we have gone through all the necessary information of orthogonal vectors and have a clear understanding of how to check whether the vectors are orthogonal or not, then let’s analyze some of the properties of the orthogonal vectors.
Perpendicular In Nature
The vectors said to be orthogonal would always be perpendicular in nature and will always yield the dot product to be 0 as being perpendicular means that they will have an angle of 90° between them.
The Zero Vector Is Orthogonal
The zero vector would always be orthogonal to every vector that the zero vector exists with. This is because any vector, when multiplied with the zero vector, would always yield the dot product to be zero.
Cross Product Of Orthogonal Vectors
The cross product of 2 orthogonal vectors can never be zero. This is because the cross product formula involves the trigonometric function sin, and the sin of 90° is always equal to 1. Hence the cross product of orthogonal vectors will never be equal to 0.
Practice Problems:
- Find whether the vectors (1, 2) and (2, -1) are orthogonal.
- Find whether the vectors (1, 0, 3) and (4, 7, 4) are orthogonal.
- Prove that the cross product of orthogonal vectors is not equal to zero.
Answers
- Yes
- No
- Prove through the cross product formula
All diagrams are constructed using GeoGebra.