JUMP TO TOPIC

What is a Vector in Geometry?

Vector Geometry – Explanation & Examples

Modeling is important in all branches of mathematics, including vector geometry. This is:

“The study of geometric representations of vectors, namely the representation as directed line
segments or arrows.”

In this topic, we will discuss the following aspects of vector geometry:

What is a Vector in Geometry?
Vector Definition in Geometry

What is a Vector in Geometry?

Quantities with both magnitude and direction are known as vectors. We can use a graph to represent vectors visually. For example, a vector connecting two points, A and B, is called:

A vector in standard position will have the origin as its starting point.

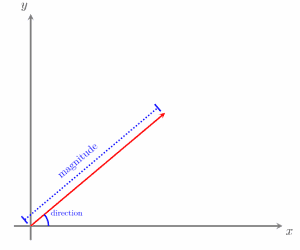
In component or column form, vectors are written in an ordered pair (x, y). A vector written in this form begins at the origin and ends at the ordered pair’s point.

The negative of a given vector is found by reversing the direction of the vector. In this case, its magnitude (or length) is the same as that of the original vector.

For example, the vector:

BA = –AB

is the negative of the vector AB, and:

||BA|| = ||-AB|| = ||AB||

Vector Definition in Geometry

Given two points, P and Q, the arrow from P to Q will have both length and direction.

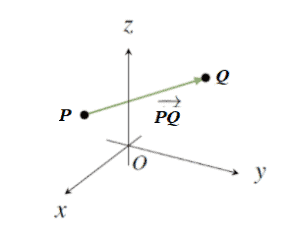
Let us assume that P and Q be two arbitrary points in space R³. The line segment from P to Q is denoted as PQ. In geometry, this is known as the vector from P to Q.

This vector will have magnitude and direction. Point P is called the tail (or the initial point) of the vector PQ, while the point Q is called the tip (or the head or the terminal point) of the vector PQ. Its length is denoted as ||PQ||.

Suppose the point P has coordinates (x₁, y₁), and the point Q has coordinates (x₂, y₂) in the plane R². Then the length of the vector PQ is defined by the steps given below.

Step 1: First, subtract the first component of point P from the first component of point Q. Then, find the square of the resulting difference.

Step 2: Similarly, subtract the second component of point P from the second component of the point Q and square that number.

Step 3: Then, add the two squares together.

Step 4: Finally, take the square root of the number you found in step three. This scalar number will be the length of the vector.

Note that the length or magnitude of a vector is a scalar quantity.

Examples

Now, let’s try a few examples to practice working with vector geometry.

Example 1

Given two points, O at the origin, (0,0), and A with the coordinates (3,2), determine the length ||OA||.

Solution:

Comparing components, we get

(x₁, y₁) = (0,0) and (x₂, y₂) = (3, 2).

Using the above-mentioned formula for finding the length of two a vector, we have:

‖OA‖ = √((x_2-x_1 )^2+(y_2 – y_1 )^2 ).

Now, substituting the above values gives us:

=√((0-3)^2+(0-2)^2 ).

Simplifying, we get:

‖OA‖ = √((-3)^2+(-2)^2 )

Additional simplification gives us:

‖OA‖ = √(9+4)

‖OA‖ = √13.

Thus, ||OA|| = √13 is the vector’s length connecting the two points.

Note that if the initial point or the tail of a vector is at the origin, i.e., if the vector is written in standard form, then the magnitude of OA is:

||A|| = √(x² + y²)

Where A = OA = (x, y).

Example 2

Given two points, A = (3, 2) and B = (2, 2), determine the vector AB length.

Solution:

Comparing components, we get

(x₁, y₁) = (3, 2) and (x₂, y₂) = (2, 2).

Using the above-mentioned formula for finding the length of two a vector, we have

‖AB‖ = √((x_2-x_1 )^2+(y_2 – y_1 )^2 )

Now, substituting the above values gives us:

‖AB‖ = √((3-2)^2+(2-2)^2 )

Simplifying, we get:

‖AB‖ = √((1)^2+(0)^2 )

‖AB‖ = √1+ 0

‖AB‖ = 1

Thus, ||AB|| = 1 is the vector’s length connecting the two points.

Example 3

In the figure below, two vectors AB = 2a and BC = 3b, are given. Point D is the midpoint of BE and E is the midpoint of BC.

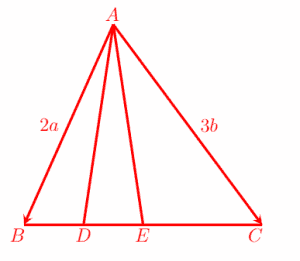
Using the information given above, determine the following vectors in terms of a and b:

(a) BC
(b) BD
(c) AD

Solution:

(a) Using the triangle law of vector addition, we have

BC = BA + AC

We note the relationship between BA and the vector of known length, AB:

= (-AB) + AC

Substituting the known values of AB and AC gives us:

= -2a + 3b.

Thus, BC = -2a + 3b is the length of the vector.

(b) Since E is given as the midpoint of BC, and D is the midpoint of BE, then D one-fourth of the distance BC:

BD = ¼ BC

Substituting the value of BC found in part (a) gives us:

= ¼ (-2a + 3b)

= -1/2 a + 3/4 b.

Thus, BD = -1/2 a + 3/4 b is the length of the vector.

AD = AB + BD

Substituting the known values of AB and AC gives us:

= 2a + (-1/2 a + 3/4 b)

This can be simplified:

= (2a + -1/2 a) + 3/4 b

= 3/2 a + 3/4 b.

Thus, AD = 3/2 a + 3/4 b is the length of the vector.

Example 4

Let A = (2, 0, -4) and B = (2, 1, -2) be two points in the space R³. If 2a – ||b||b = 3/2 (a – 2x), where a = OA, b = OB and x = OX and X = (x₁, x₂, x₃), find the values of x₁, x₂ and x₃.

Solution:

We are given the relationship:

2a – ||b||b = 3/2 (a – 2x),

Where a = (2, 0, -4), b = (2, 1, -2) and x = (x₁, x₂, x₃).

Firstly we will evaluate the norm (magnitude) ||b|| by using previous definitions and the procedure for finding the magnitude of a vector whose starting point is at the origin. This gives us:

||b|| = √(2² + 1² + (-2)²)

= √(4 + 1 + 4)

= √9

Therefore, ||b|| = 3. Now we have:

||b|| b = 3 (2, 1, -2)

= (3∙2, 3∙1, 3∙(-2))

= (6, 3, -6)

Similarly, we have:

2a = 2 (2, 0, -4) = (4, 0, -8).

Therefore, the left-hand side will become

2a – ||b||b = (4, 0, -8) – (6, 3, -6)

= (4-6, 0-3 , -8-(-6))

= (-2, -3, -8+6)

= (-2, -3, -2).

The right-hand side will become:

3/2 (a – 2x) = 3/2 ((4, 0, -8)– 2(x₁, x₂, x₃))

= 3/2 ((4, 0, -8) – (2x₁, 2x₂, 2x₃))

= 3/2 (4-2x₁, 2x₂, -8-2x₃).

Now substituting these values into the left- and right-hand sides of the equation, we get:

2a – ||b||b = 3/2 (a – 2x)

(-2, -3, -2) = 3/2 (4-2x₁, 2x₂, -8-2x₃)

2 (-2, -3, -2) = 3 (4-2x₁, 2x₂, -8-2x₃)

(-4, -6, -4) = (3(4-2x₁), 3(2x₂), 3(-8-2x₃)).

Comparing the x, y, and z components give us:

-4 = 3(4-2x₁)

-4= 12 – 6x₁

6x₁ =12 – 4

6x₁= 8

x₁ = 8/6

Therefore, x₁= 4/3.

-6 = 3(2x₂)

-6= 6x₂

x₂ = -6/6

Therefore, x₂= -1

-4 = 3(-8-2x₃)

-4= -24 -6x₃

6x₃ = -24 + 4

6x₃= -20

x₃ = -20/6

Therefore, x₃= -10/3.

Thus:

x₁ = 4/3, x₂ = -1, and x₃ = -10/3.

Practice Questions

Given two points, V = (2, 5, 1) and C = (3, -2, 1), determine the length of the vector VC.
Given two points, G = (5, 5) and H = (4, -10), determine ||OG|| and ||OH||², where O = (0, 0) is the origin.
In the triangle ABC, CB = 4CX, XA = 5XY, and Z is the midpoint of AB. Let CX = m and BZ = n.

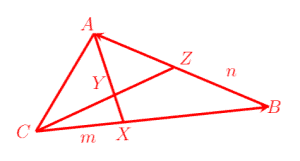
(a) Determine the length of XB and XA in terms of m and n
(b) Show that CZ = (4m+n)
(c) Evaluate ‖CY‖/‖CZ‖ and (area ACY)/(area ACZ)

Let ABCDEF be a regular hexagon, and let AB = n.

(a) Explain why the vector ED = n.
(b) If BC = m and CD = p, find AC and AD
(c) Find FD.

Given a straight line ABC, let BC = 3AB. If OA = a and AB = b, express OC in terms of a and b.

Answers

||VC|| = 5√2
||OG|| = 5√2, ||OH||² = 116
In the given triangle,

(a) XB = 3m and XA=3m + 2n
(b) CZ=CB+BZ=4m+n
(c) The values are: ‖CY‖/‖CZ‖ = 2/5, and (area ACY)/(area ACZ) = 2/5

4. Let ABCDEF be a regular hexagon and AB = n.

(a) It is opposite AB.
(b) If BC = m and CD = p. Then AC = n+m and AD = n+m+p
(c) FD = -(m+n) (i.e, negative of the vector AC).

OC = a+4b

Vector Geometry – Explanation & Examples

What is a Vector in Geometry?

Vector Definition in Geometry

Examples

Practice Questions

Previous Lesson | Main Page | Next Lesson