Julia Robinson and Yuri Matiyasevich: Computability Theory & Computational Complexity Theory
 |
Julia Robinson (1919-1985) and Yuri Matiyasevich (1947- ) |
In a field almost completely dominated by men, Julia Robinson was one of the very few women to have made a serious impact on mathematics – others who merit mention are Sophie Germain and Sofia Kovalevskaya in the 19th Century, and Alicia Stout and Emmy Noether in the 20th – and she became the first women to be elected as president of the American Mathematical Society.
Julia Robinson Biography
Brought up in the deserts of Arizona, Robinson was a shy and sickly child but showed an innate love for, and facility with, numbers from an early age. She had to overcome many obstacles and to fight to be allowed to continue studying mathematics, but she persevered, obtained her PhD at Berkeley and married a mathematician, her Berkeley professor, Raphael Robinson.
She spent most of her career pursuing computability and “decision problems”, questions in formal systems with “yes” or “no” answers, depending on the values of some input parameters. Her particular passion was Hilbert’s tenth problem, and she applied herself to it obsessively. The problem was to ascertain whether there was any way of telling whether or not any particular Diophantine equation (a polynomial equation whose variables can only be integers) had whole number solutions. The growing belief was that no such universal method was possible, but it seemed very difficult to actually prove that it would NEVER be possible to come up with such a method.
Throughout the 1950s and 1960s, Robinson, along with her colleagues Martin Davis and Hilary Putnam, doggedly pursued the problem, and eventually developed what became known as the Robinson hypothesis, which suggested that, in order to show that no such method existed, all that was needed was to construct one equation whose solution was a very specific set of numbers, one which grew exponentially.
The problem had obsessed Robinson for over twenty years and she confessed to a desperate desire to see its solution before she died, whoever might achieve it.
In order to progress further, though, she needed input from the young Russian mathematician, Yuri Matiyasevich.
Born and educated in Leningrad (St. Petersburg), Matiyasevich had already distinguished himself as a mathematical prodigy, and won numerous prizes in mathematics. He turned to Hilbert’s tenth problem as the subject of his doctoral thesis at Leningrad State University, and began to correspond with Robinson about her progress, and to search for a way forward.
After pursuing the problem during the late 1960s, Matiyasevich finally discovered the final missing piece of the jigsaw in 1970, when he was just 22 years old. He saw how he could capture the famous Fibonacci sequence of numbers using the equations that were at the heart of Hilbert’s tenth problem, and so, building on Robinson’s earlier work, it was finally proved that it is in fact impossible to devise a process by which it can be determined in a finite number of operations whether Diophantine equations are solvable in rational integers.
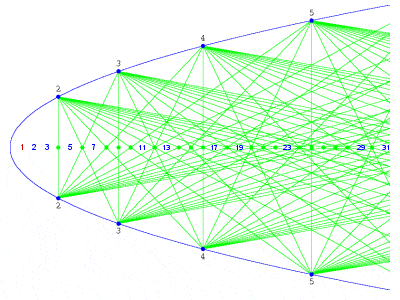 |
Matiyasevich-Stechkin visual sieve for prime numbers |
In a poignant example of the internationalism of mathematics at the height of the Cold War, Matiyasevich freely acknowledged his debt to Robinson’s work, and the two went on to work together on other problems until Robinson’s death in 1984.
Matiyasevich-Stechkin visual sieve for prime numbers
Among, his other achievements, Matiyasevich and his colleague Boris Stechkin also developed an interesting “visual sieve” for prime numbers, which effectively “crosses out” all the composite numbers, leaving only the primes. He has a theorem on recursively enumerable sets named after him, as well as a polynomial related to the colourings of triangulation of spheres.
He is head of the Laboratory of Mathematical Logic at the St. Petersburg Department of the Steklov Institute of Mathematics of Russian Academy of Sciences, and is a member of several mathematical societies and boards.
<< Back to Cohen |
