HURT GÖDEL: THE ECCENTRIC GENIUS
Biography
 |
Kurt Gödel (1906-1978) |
Kurt Gödel grew up a rather strange, sickly child in Vienna. From an early age his parents took to referring to him as “Herr Varum”, Mr Why, for his insatiable curiosity. At the University of Vienna, Gödel first studied number theory, but soon turned his attention to mathematical logic, which was to consume him for most of the rest of his life. As a young man, he was, like Hilbert, optimistic and convinced that mathematics could be made whole again, and would recover from the uncertainties introduced by the work of Cantor and Riemann.
Between the wars, Gödel joined in the cafe discussions of a group of intense intellectuals and philosophers known as the Vienna Circle, which included logical positivists such as Moritz Schlick, Hans Hahn and Rudolf Carnap, who rejected metaphysics as meaningless and sought to codify all knowledge in a single standard language of science.
Although Gödel did not necessarily share the positivistic philosophical outlook of the Vienna Circle, it was in this enviroment that Gödel pursued his dream of solving the second, and perhaps most overarching, of Hilbert’s 23 problems, which sought to find a logical foundation for all of mathematics. The ideas he came up with would revolutionize mathematics, as he effectively proved, mathematically and philosophically, that Hilbert’s (and his own) optimism was unfounded and that such a foundation was just not possible.
His first achievement, which actually served to advance Hilbert‘s Program, was his completeness theorem, which showed that all valid statements in Freges’s “first order logic” can be proved from a set of simple axioms. However, he then turned his attention to “second order logic“, i.e a logic powerful enough to support arithmetic and more complex mathematical theories (essentially, one able to accept sets as values of variables).
Incompleteness Theorem
Gödel’s incompleteness theorem (technically “incompleteness theorems“, plural, as there were actually two separate theorems, although they are usually spoken of together) of 1931 showed that, within any logical system for mathematics (or at least in any system that is powerful and complex enough to be able to describe the arithmetic of the natural numbers, and therefore to be interesting to most mathematicians), there will be some statements about numbers which are true but which can NEVER be proved. This was enough to prompt John von Neumann to comment that “it’s all over“.
 |
Gödel’s Incompleteness Theorem |
His approach began with the plain language assertion such as “this statement cannot be proved”, a version of the ancient “liar paradox”, and a statement which itself must be either true or false. If the statement is false, then that means that the statement can be proved, suggesting that it is actually true, thus generating a contradiction. For this to have implications in mathematics, though, Gödel needed to convert the statement into a “formal language” (i.e. a pure statement of arithmetic). He did this using a clever code based on prime numbers, where strings of primes play the roles of natural numbers, operators, grammatical rules and all the other requirements of a formal language. The resulting mathematical statement therefore appears, like its natural language equivalent, to be true but unprovable, and must therefore remain undecided.
The incompleteness theorem – surely a mathematician’s worst nightmare – led to something of a crisis in the mathematical community, raising the spectre of a problem which may turn out to be true but is still unprovable, something which had not been even considered in the whole two millennia plus history of mathematics. Gödel effectively put paid, at a stroke, to the ambitions of mathematicians like Bertrand Russell and David Hilbert who sought to find a complete and consistent set of axioms for all of mathematics. His work PROVED that any system of logic or numbers that mathematicians ever come up with will always rest on at least a few unprovable assumptions. His conclusions also imply that not all mathematical questions are even computable, and that it is impossible, even in principle, to create a machine or computer that will be able to do all that a human mind can do.
Gödel Metric
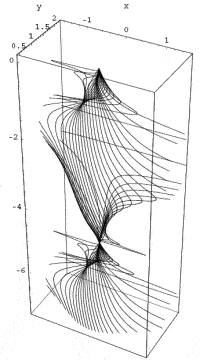 |
Representation of the Gödel Metric, an exact solution to Einstein’s field equations |
Unfortunately, the theorems also led to a personal crisis for Gödel. In the mid 1930s, he suffered a series of mental breakdowns and spent some significant time in a sanatorium. Nevertheless, he threw himself into the same problem that had destroyed the mental well-being of Georg Cantor during the previous century, the continuum hypothesis. In fact, he made an important step in the resolution of that notoriously difficult problem (by proving that the the axiom of choice is independence from finite type theory), without which Paul Cohen would probably never have been able to come to his definitive solution. Like Cantor and others after him, though, Gödel too suffered a gradual deterioration in his mental and physical health.
He was only kept afloat at all by the love of his life, Adele Numbursky. Together, they witnessed the virtual destruction of the German and Austrian mathematics community by the Nazi regime. Eventually, along with many other eminent European mathematicians and scholars, Gödel fled the Nazis to the safety of Princeton in the USA, where he became a close friend of fellow exile Albert Einstein, contributing some demonstrations of paradoxical solutions to Einstein’s field equations in general relativity (including his celebrated Gödel metric of 1949).
But, even in the USA, he was not able to escape his demons, and was dogged by depression and paranoia, suffering several more nervous breakdowns. Eventually, he would only eat food that had been tested by his wife Adele, and, when Adele herself was hospitalized in 1977, Gödel simply refused to eat and starved himself to death.
Gödel’s legacy is ambivalent. Although he is recognized as one of the great logicians of all time, many were just not prepared to accept the almost nihilistic consequences of his conclusions, and his explosion of the traditional formalist view of mathematics. Worse news was still to come, though, as the mathematical community (including, as we will see, Alan Turing) struggled to come to grips with Gödel’s findings.
<< Back to Hilbert | Forward to Turing >> |
