18TH CENTURY MATHEMATICS
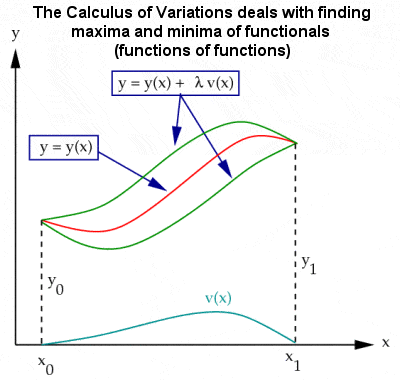 |
Calculus of variations |
Most of the late 17th Century and a good part of the early 18th were taken up by the work of disciples of Newton and Leibniz, who applied their ideas on calculus to solving a variety of problems in physics, astronomy and engineering.
The period was dominated, though, by one family, the Bernoulli’s of Basel in Switzerland, which boasted two or three generations of exceptional mathematicians, particularly the brothers, Jacob and Johann. They were largely responsible for further developing Leibniz’s infinitesimal calculus – paricularly through the generalization and extension of calculus known as the “calculus of variations” – as well as Pascal and Fermat’s probability and number theory.
Basel was also the home town of the greatest of the 18th Century mathematicians, Leonhard Euler, although, partly due to the difficulties in getting on in a city dominated by the Bernoulli family, Euler spent most of his time abroad, in Germany and St. Petersburg, Russia. He excelled in all aspects of mathematics, from geometry to calculus to trigonometry to algebra to number theory, and was able to find unexpected links between the different fields. He proved numerous theorems, pioneered new methods, standardized mathematical notation and wrote many influential textbooks throughout his long academic life.
In a letter to Euler in 1742, the German mathematician Christian Goldbach proposed the Goldbach Conjecture, which states that every even integer greater than 2 can be expressed as the sum of two primes (e.g. 4 = 2 + 2; 8 = 3 + 5; 14 = 3 + 11 = 7 + 7; etc) or, in another equivalent version, every integer greater than 5 can be expressed as the sum of three primes. Yet another version is the so-called “weak” Goldbach Conjecture, that all odd numbers greater than 7 are the sum of three odd primes. They remain among the oldest unsolved problems in number theory (and in all of mathematics), although the weak form of the conjecture appears to be closer to resolution than the strong one. Goldbach also proved other theorems in number theory such as the Goldbach-Euler Theorem on perfect powers.
Despite Euler’s and the Bernoullis’ dominance of 18th Century mathematics, many of the other important mathematicians were from France. In the early part of the century, Abraham de Moivre is perhaps best known for de Moivre’s formula, (cosx + isinx)n = cos(nx) + isin(nx), which links complex numbers and trigonometry. But he also generalized Newton’s famous binomial theorem into the multinomial theorem, pioneered the development of analytic geometry, and his work on the normal distribution (he gave the first statement of the formula for the normal distribution curve) and probability theory were of great importance.
France became even more prominent towards the end of the century, and a handful of late 18th Century French mathematicians in particular deserve mention at this point, beginning with “the three L’s”.
Joseph Louis Lagrange collaborated with Euler in an important joint work on the calculus of variation, but he also contributed to differential equations and number theory, and he is usually credited with originating the theory of groups, which would become so important in 19th and 20th Century mathematics. His name is given an early theorem in group theory, which states that the number of elements of every sub-group of a finite group divides evenly into the number of elements of the original finite group.
Lagrange’s Mean value Theorem
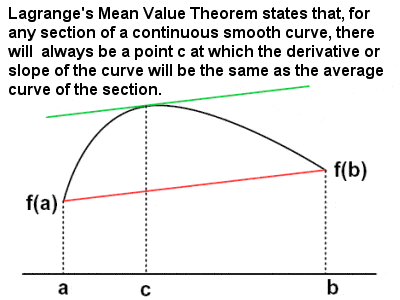 |
Lagrange’s Mean value Theorem |
Lagrange is also credited with the four-square theorem, that any natural number can be represented as the sum of four squares (e.g. 3 = 12 + 12 + 12 + 02; 31 = 52 + 22 + 12 + 12; 310 = 172 + 42 + 22 + 12; etc), as well as another theorem, confusingly also known as Lagrange’s Theorem or Lagrange’s Mean Value Theorem, which states that, given a section of a smooth continuous (differentiable) curve, there is at least one point on that section at which the derivative (or slope) of the curve is equal (or parallel) to the average (or mean) derivative of the section. Lagrange’s 1788 treatise on analytical mechanics offered the most comprehensive treatment of classical mechanics since Newton, and formed a basis for the development of mathematical physics in the 19th Century.
Pierre-Simon Laplace, sometimes referred to as “the French Newton”, was an important mathematician and astronomer, whose monumental work “Celestial Mechanics” translated the geometric study of classical mechanics to one based on calculus, opening up a much broader range of problems. Although his early work was mainly on differential equations and finite differences, he was already starting to think about the mathematical and philosophical concepts of probability and statistics in the 1770s, and he developed his own version of the so-called Bayesian interpretation of probability independently of Thomas Bayes. Laplace is well known for his belief in complete scientific determinism, and he maintained that there should be a set of scientific laws that would allow us – at least in principle – to predict everything about the universe and how it works.
The first six Legendre polynomials
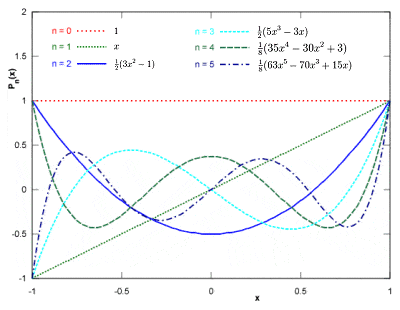 |
The first six Legendre polynomials (solutions to Legendre’s differential equation) |
Adrien-Marie Legendre also made important contributions to statistics, number theory, abstract algebra and mathematical analysis in the late 18th and early 19th Centuries, athough much of his work (such as the least squares method for curve-fitting and linear regression, the quadratic reciprocity law, the prime number theorem and his work on elliptic functions) was only brought to perfection – or at least to general notice – by others, particularly Gauss. His “Elements of Geometry”, a re-working of Euclid’s book, became the leading geometry textbook for almost 100 years, and his extremely accurate measurement of the terrestrial meridian inspired the creation, and almost universal adoption, of the metric system of measures and weights.
Yet another Frenchman, Gaspard Monge was the inventor of descriptive geometry, a clever method of representing three-dimensional objects by projections on the two-dimensional plane using a specific set of procedures, a technique which would later become important in the fields of engineering, architecture and design. His orthographic projection became the graphical method used in almost all modern mechanical drawing.
After many centuries of increasingly accurate approximations, Johann Lambert, a Swiss mathematician and prominent astronomer, finally provided a rigorous proof in 1761 that π is irrational, i.e. it can not be expressed as a simple fraction using integers only or as a terminating or repeating decimal. This definitively proved that it would never be possible to calculate it exactly, although the obsession with obtaining more and more accurate approximations continues to this day. (Over a hundred years later, in 1882, Ferdinand von Lindemann would prove that π is also transcendental, i.e. it cannot be the root of any polynomial equation with rational coefficients). Lambert was also the first to introduce hyperbolic functions into trigonometry and made some prescient conjectures regarding non-Euclidean space and the properties of hyperbolic triangles.
<< Back to Leibniz | Forward to Bernoulli Brothers >> |
