LEONHARD EULER – SWISS MATHEMATICIAN
 |
Leonhard Euler (1707-1783) |
Leonhard Euler was one of the giants of 18th Century mathematics. Like the Bernoulli’s, he was born in Basel, Switzerland, and he studied for a while under Johann Bernoulli at Basel University. But, partly due to the overwhelming dominance of the Bernoulli family in Swiss mathematics, and the difficulty of finding a good position and recognition in his hometown, he spent most of his academic life in Russia and Germany, especially in the burgeoning St. Petersburg of Peter the Great and Catherine the Great.
Despite a long life and thirteen children, Euler had more than his fair share of tragedies and deaths, and even his blindness later in life did not slow his prodigious output – his collected works comprise nearly 900 books and, in the year 1775, he is said to have produced on average one mathematical paper every week – as he compensated for it with his mental calculation skills and photographic memory (for example, he could repeat the Aeneid of Virgil from beginning to end without hesitation, and for every page in the edition he could indicate which line was the first and which the last).
Today, Euler is considered one of the greatest mathematicians of all time. His interests covered almost all aspects of mathematics, from geometry to calculus to trigonometry to algebra to number theory, as well as optics, astronomy, cartography, mechanics, weights and measures and even the theory of music.
Mathematical notation created or popularized by Euler
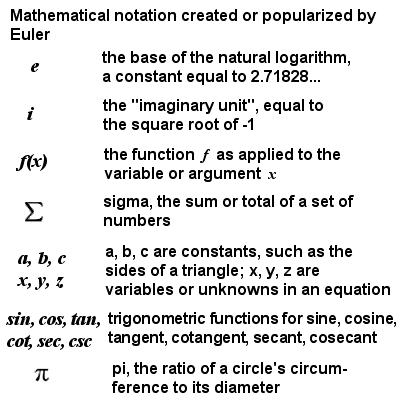 |
Mathematical notation created or popularized by Euler |
Much of the notation used by mathematicians today – including e, i, f(x), ∑, and the use of a, b and c as constants and x, y and z as unknowns – was either created, popularized or standardized by Euler. His efforts to standardize these and other symbols (including π and the trigonometric functions) helped to internationalize mathematics and to encourage collaboration on problems.
He even managed to combine several of these together in an amazing feat of mathematical alchemy to produce one of the most beautiful of all mathematical equations, eiπ = -1, sometimes known as Euler’s Identity. This equation combines arithmetic, calculus, trigonometry and complex analysis into what has been called “the most remarkable formula in mathematics”, “uncanny and sublime” and “filled with cosmic beauty”, among other descriptions. Another such discovery, often known simply as Euler’s Formula, is eix = cosx + isinx. In fact, in a recent poll of mathematicians, three of the top five most beautiful formulae of all time were Euler’s. He seemed to have an instinctive ability to demonstrate the deep relationships between trigonometry, exponentials and complex numbers.
The discovery that initially sealed Euler’s reputation was announced in 1735 and concerned the calculation of infinite sums. It was called the Basel problem after the Bernoulli’s had tried and failed to solve it, and asked what was the precise sum of the of the reciprocals of the squares of all the natural numbers to infinity i.e. 1⁄12 + 1⁄22 + 1⁄32 + 1⁄42 … (a zeta function using a zeta constant of 2). Euler’s friend Daniel Bernoulli had estimated the sum to be about 13⁄5, but Euler’s superior method yielded the exact but rather unexpected result of π2⁄6. He also showed that the infinite series was equivalent to an infinite product of prime numbers, an identity which would later inspire Riemann’s investigation of complex zeta functions.
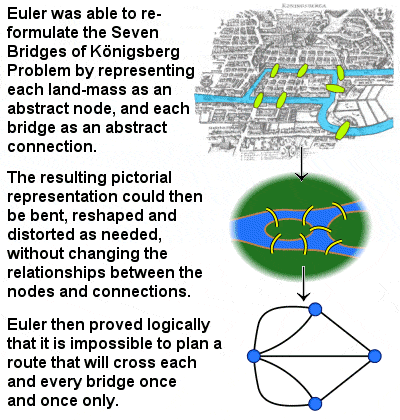
The Seven Bridges of Königsberg Problem
 |
The Seven Bridges of Königsberg Problem |
Also in 1735, Euler solved an intransigent mathematical and logical problem, known as the Seven Bridges of Königsberg Problem, which had perplexed scholars for many years, and in doing so laid the foundations of graph theory and presaged the important mathematical idea of topology. The city of Königsberg in Prussia (modern-day Kaliningrad in Russia) was set on both sides of the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges. The problem was to find a route through the city that would cross each bridge once and only once.
In fact, Euler proved that the problem has no solution, but in doing so he made the important conceptual leap of pointing out that the choice of route within each landmass is irrelevant and the only important feature is the sequence of bridges crossed. This allowed him to reformulate the problem in abstract terms, replacing each land mass with an abstract node and each bridge with an abstract connection. This resulted in a mathematical structure called a “graph”, a pictorial representation made up of points (vertices) connected by non-intersecting curves (arcs), which may be distorted in any way without changing the graph itself.
In this way, Euler was able to deduce that, because the four land masses in the original problem are touched by an odd number of bridges, the existence of a walk traversing each bridge once only inevitably leads to a contradiction. If Königsberg had had one fewer bridges, on the other hand, with an even number of bridges leading to each piece of land, then a solution would have been possible.
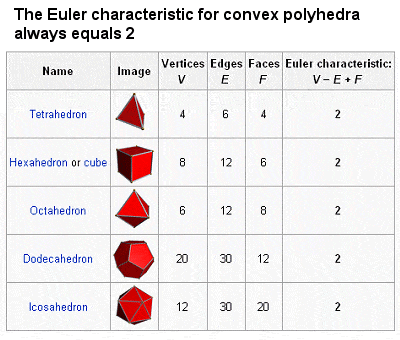
List of theorems and methods pioneered by Euler
 |
The Euler Characteristic |
The list of theorems and methods pioneered by Euler is immense, and largely outside the scope of an entry-level study such as this, but mention could be made of just some of them:
- the demonstration of geometrical properties such as Euler’s Line and Euler’s Circle;
- the definition of the Euler Characteristic χ (chi) for the surfaces of polyhedra, whereby the number of vertices minus the number of edges plus the number of faces always equals 2 (see table at right);
- a new method for solving quartic equations;
- the Prime Number Theorem, which describes the asymptotic distribution of the prime numbers;
- proofs (and in some cases disproofs) of some of Fermat’s theorems and conjectures;
- the discovery of over 60 amicable numbers (pairs of numbers for which the sum of the divisors of one number equals the other number), although some were actually incorrect;
- a method of calculating integrals with complex limits (foreshadowing the development of modern complex analysis);
- the calculus of variations, including its best-known result, the Euler-Lagrange equation; a proof of the infinitude of primes, using the divergence of the harmonic series;
- the integration of Leibniz‘s differential calculus with Newton‘s Method of Fluxions into a form of calculus we would recognize today, as well as the development of tools to make it easier to apply calculus to real physical problems;
- etc, etc.
In 1766, Euler accepted an invitation from Catherine the Great to return to the St. Petersburg Academy, and spent the rest of his life in Russia. However, his second stay in the country was marred by tragedy, including a fire in 1771 which cost him his home (and almost his life), and the loss in 1773 of his dear wife of 40 years, Katharina. He later married Katharina’s half-sister, Salome Abigail, and this marriage would last until his death from a brain hemorrhage in 1783.
<< Back to Bernoulli Brothers | Forward to 19th Century Mathematics >> |
