CARL FRIEDRICH GAUSS – The Prince of Mathematics

Carl Friedrich Gauss (1777-1855)

Biography

Johann Carl Friedrich Gauss is sometimes referred to as the “Prince of Mathematicians” and the “greatest mathematician since antiquity”. He has had a remarkable influence in many fields of mathematics and science and is ranked as one of history’s most influential mathematicians.

Gauss was a child prodigy. There are many anecdotes concerning his precocity as a child, and he made his first ground-breaking mathematical discoveries while still a teenager.

At just three years old, he corrected an error in his father payroll calculations, and he was looking after his father’s accounts on a regular basis by the age of 5. At the age of 7, he is reported to have amazed his teachers by summing the integers from 1 to 100 almost instantly (having quickly spotted that the sum was actually 50 pairs of numbers, with each pair summing to 101, total 5,050). By the age of 12, he was already attending gymnasium and criticizing Euclid’s geometry.

Although his family was poor and working class, Gauss’ intellectual abilities attracted the attention of the Duke of Brunswick, who sent him to the Collegium Carolinum at 15, and then to the prestigious University of Göttingen (which he attended from 1795 to 1798). It was as a teenager attending university that Gauss discovered (or independently rediscovered) several important theorems.

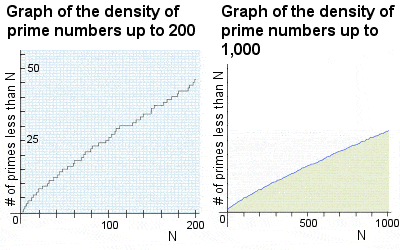Graphs of the density of prime numbers

At 15, Gauss was the first to find any kind of a pattern in the occurrence of prime numbers, a problem which had exercised the minds of the best mathematicians since ancient times. Although the occurrence of prime numbers appeared to be almost competely random, Gauss approached the problem from a different angle by graphing the incidence of primes as the numbers increased. He noticed a rough pattern or trend: as the numbers increased by 10, the probability of prime numbers occurring reduced by a factor of about 2 (e.g. there is a 1 in 4 chance of getting a prime in the number from 1 to 100, a 1 in 6 chance of a prime in the numbers from 1 to 1,000, a 1 in 8 chance from 1 to 10,000, 1 in 10 from 1 to 100,000, etc). However, he was quite aware that his method merely yielded an approximation and, as he could not definitively prove his findings, and kept them secret until much later in life.

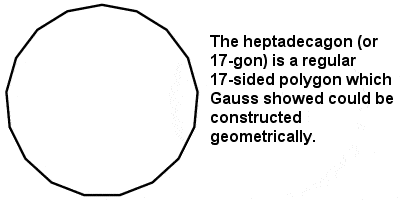17-sided heptadecagon constructed by Gauss

In Gauss’s annus mirabilis of 1796, at just 19 years of age, he constructed a hitherto unknown regular seventeen-sided figure using only a ruler and compass, a major advance in this field since the time of Greek mathematics, formulated his prime number theorem on the distribution of prime numbers among the integers, and proved that every positive integer is representable as a sum of at most three triangular numbers.

Gauss Theory

Although he made contributions in almost all fields of mathematics, number theory was always Gauss’ favourite area, and he asserted that “mathematics is the queen of the sciences, and the theory of numbers is the queen of mathematics”. An example of how Gauss revolutionized number theory can be seen in his work with complex numbers (combinations of real and imaginary numbers).

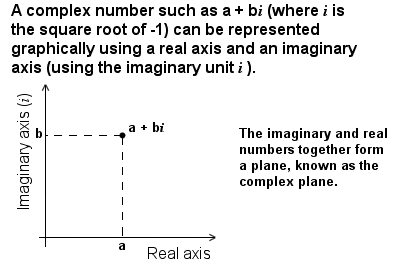Representation of complex numbers

Gauss gave the first clear exposition of complex numbers and of the investigation of functions of complex variables in the early 19th Century. Although imaginary numbers involving i (the imaginary unit, equal to the square root of -1) had been used since as early as the 16th Century to solve equations that could not be solved in any other way, and despite Euler’s ground-breaking work on imaginary and complex numbers in the 18th Century, there was still no clear picture of how imaginary numbers connected with real numbers until the early 19th Century. Gauss was not the first to intepret complex numbers graphically (Jean-Robert Argand produced his Argand diagrams in 1806, and the Dane Caspar Wessel had described similar ideas even before the turn of the century), but Gauss was certainly responsible for popularizing the practice and also formally introduced the standard notation a + bi for complex numbers. As a result, the theory of complex numbers received a notable expansion, and its full potential began to be unleashed.

At the age of just 22, he proved what is now known as the Fundamental Theorem of Algebra (although it was not really about algebra). The theorem states that every non-constant single-variable polynomial over the complex numbers has at least one root (although his initial proof was not rigorous, he improved on it later in life). What it also showed was that the field of complex numbers is algebraically “closed” (unlike real numbers, where the solution to a polynomial with real co-efficients can yield a solution in the complex number field).

Then, in 1801, at 24 years of age, he published his book “Disquisitiones Arithmeticae”, which is regarded today as one of the most influential mathematics books ever written, and which laid the foundations for modern number theory. Among many other things, the book contained a clear presentation of Gauss’ method of modular arithmetic, and the first proof of the law of quadratic reciprocity (first conjectured by Euler and Legendre).

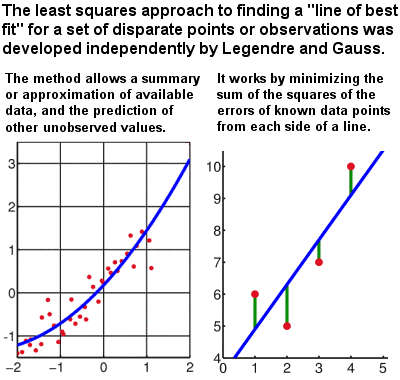Line of best fit by Gauss’ least squares method

For much of his life, Gauss also retained a strong interest in theoretical astrononomy, and he held the post of Director of the astronomical observatory in Göttingen for many years. When the planetoid Ceres was in the process of being identified in the late 17th Century, Gauss made a prediction of its position which varied greatly from the predictions of most other astronomers of the time. But, when Ceres was finally discovered in 1801, it was almost exacly where Gauss had predicted. Although he did not explain his methods at the time, this was one of the first applications of the least squares approximation method, usually attributed to Gauss, although also claimed by the Frenchman Legendre. Gauss claimed to have done the logarithmic calculations in his head.

As Gauss’ fame spread, though, and he became known throughout Europe as the go-to man for complex mathematical questions, his character deteriorated and he became increasingly arrogant, bitter, dismissive and unpleasant, rather than just shy. There are many stories of the way in which Gauss had dismissed the ideas of young mathematicians or, in some cases, claimed them as his own.

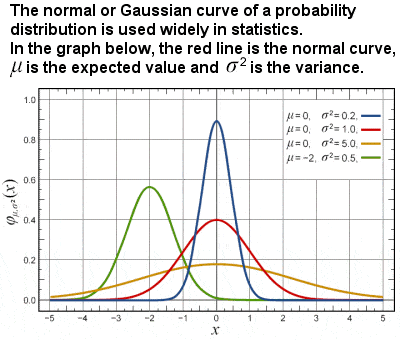Gaussian, or normal, probability curve

In the area of probability and statistics, Gauss introduced what is now known as Gaussian distribution, the Gaussian function and the Gaussian error curve. He showed how probability could be represented by a bell-shaped or “normal” curve, which peaks around the mean or expected value and quickly falls off towards plus/minus infinity, which is basic to descriptions of statistically distributed data.

He also made ths first systematic study of modular arithmetic – using integer division and the modulus – which now has applications in number theory, abstract algebra, computer science, cryptography, and even in visual and musical art.

While engaged on a rather banal surveying job for the Royal House of Hanover in the years after 1818, Gauss was also looking into the shape of the Earth, and starting to speculate on revolutionary ideas like shape of space itself. This led him to question one of the central tenets of the whole of mathematics, Euclidean geometry, which was clearly premised on a flat, and not a curved, universe. He later claimed to have considered a non-Euclidean geometry (in which Euclid‘s parallel axiom, for example, does not apply), which was internally consistent and free of contradiction, as early as 1800. Unwilling to court controversy, however, Gauss decided not to pursue or publish any of his avant-garde ideas in this area, leaving the field open to Bolyai and Lobachevsky, although he is still considered by some to be a pioneer of non-Euclidean geometry.

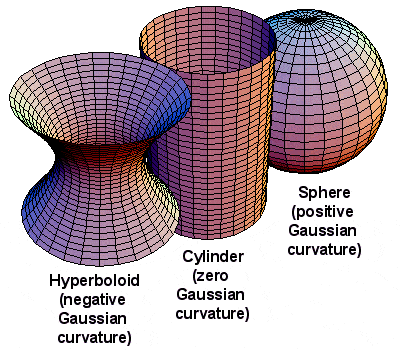Gaussian curvature

The Hanover survey work also fuelled Gauss’ interest in differential geometry (a field of mathematics dealing with curves and surfaces) and what has come to be known as Gaussian curvature (an intrinsic measure of curvature, dependent only on how distances are measured on the surface, not on the way it is embedded in space). All in all, despite the rather pedestrian nature of his employment, the responsibilities of caring for his sick mother and the constant arguments with his wife Minna (who desperately wanted to move to Berlin), this was a very fruitful period of his academic life, and he published over 70 papers between 1820 and 1830.

Gauss’ achievements were not limited to pure mathematics, however. During his surveying years, he invented the heliotrope, an instrument that uses a mirror to reflect sunlight over great distances to mark positions in a land survey. In later years, he collaborated with Wilhelm Weber on measurements of the Earth’s magnetic field, and invented the first electric telegraph. In recognition of his contributions to the theory of electromagnetism, the international unit of magnetic induction is known as the gauss.