DAVID HILBERT’S CONTRIBUTIONS TO LOGICAL THEORY
Biography
 |
David Hilbert (1862-1943) |
David Hilbert was a great leader and spokesperson for the discipline of mathematics in the early 20th Century. But he was an extremely important and respected mathematician in his own right.
Like so many great German mathematicians before him, Hilbert was another product of the University of Göttingen, at that time the mathematical centre of the world, and he spent most of his working life there. His formative years, though, were spent at the University of Königsberg, where he developed an intense and fruitful scientific exchange with fellow mathematicians Hermann Minkowski and Adolf Hurwitz.
Sociable, democratic and well-loved both as a student and as a teacher, and often seen as bucking the trend of the formal and elitist system of German mathematics, Hilbert’s mathematical genius nevertheless spoke for itself. He has many mathematical terms named after him, including Hilbert space (an infinite dimensional Euclidean space), Hilbert curves, the Hilbert classification and the Hilbert inequality, as well as several theorems, and he gradually established himself as the most famous mathematician of his time.
His pithy enumeration of the 23 most important open mathematical questions at the 1900 Paris conference of the International Congress of Mathematicians at the Sorbonne set the stage for almost the whole of 20th Century mathematics. The details of some of these individual problems are highly technical; some are very precise, while some are quite vague and subject to interpretation; several problems have now already been solved, or at least partially solved, while some may be forever unresolvable as stated; some relate to rather abstruse backwaters of mathematical thought, while some deal with more mainstream and well-known issues such as the Riemann hypothesis, the continuum hypothesis, group theory, theories of quadratic forms, real algebraic curves, etc.
Hilbert’s Algorithm
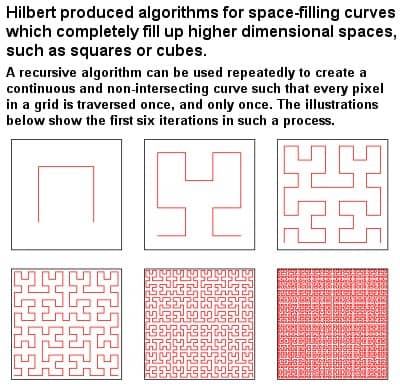 |
Hilbert’s algorithm for space-filling curves |
As a young man, Hilbert began by pulling together all of the may strands of number theory and abstract algebra, before changing field completely to pursue studies in integral equations, where he revolutionized the then current practices. In the early 1890s, he developed continuous fractal space-filling curves in multiple dimensions, building on earlier work by Giuseppe Peano. As early as 1899, he proposed a whole new formal set of geometrical axioms, known as Hilbert’s axioms, to substitute the traditional axioms of Euclid.
But perhaps his greatest legacy is his work on equations, often referred to as his finiteness theorem. He showed that although there were an infinite number of possible equations, it was nevertheless possible to split them up into a finite number of types of equations which could then be used, almost like a set of building blocks, to produce all the other equations.
Interestingly, though, Hilbert could not actually construct this finite set of equations, just prove that it must exist (sometimes referred to as an existence proof, rather than constructive proof). At the time, some critics passed this off as mere theology or smoke-and-mirrors, but it effectively marked the beginnings of a whole new style of abstract mathematics.
Hilbert Space
 |
Among other things, Hilbert space can be used to study the harmonics of vibrating strings |
This use of an existence proof rather than constructive proof was also implicit in his development, during the first decade of the 20th Century, of the mathematical concept of what came to be known as Hilbert space.
Hilbert space is a generalization of the notion of Euclidean space which extends the methods of vector algebra and calculus to spaces with any finite (or even infinite) number of dimensions. Hilbert space provided the basis for important contributions to the mathematics of physics over the following decades, and may still offer one of the best mathematical formulations of quantum mechanics.
Hilbert was unfailingly optimistic about the future of mathematics, never doubting that his 23 problems would soon be solved. In fact, he went so far as to claim that there are absolutely no unsolvable problems – a famous quote of his (dating from 1930, and also engraved on his tombstone) proclaimed, “We must know! We will know!” – and he was convinced that the whole of mathematics could, and ultimately would, be put on unshakable logical foundations. Another of his rallying cries was “in mathematics there is no ignorabimus”, a reference to the traditional position on the limits of scientific knowledge.
Unlike Russell, Hilbert’s formalism was premised on the idea that the ultimate base of mathematics lies, not in logic itself, but in a simpler system of pre-logical symbols which can be collected together in strings or axioms and manipulated according to a set of “rules of inference”. His ambitious program to find a complete and consistent set of axioms for all of mathematics (which became known as Hilbert’s Program), received a severe set-back, however, with the incompleteness theorems of Kurt Gödel in the early 1930s. Nevertheless, Hilbert’s work had started logic on a course of clarification, and the need to understand Gödel‘s work then led to the development of recursion theory and mathematical logic as an autonomous discipline in the 1930s, and later provided the basis for theoretical computer science.
For a time, Hilbert bravely spoke out against the Nazi repression of his Jewish mathematician friends in Germany and Austria in the mid 1930s. But, after mass evictions, several suicides, many deaths in concentration camps, and even direct assassinations, he too eventually lapsed into silence, and could only watch as one of the greatest mathematical centres of all time was systematically destroyed. By the time of his death in 1943, little remained of the great mathematics community at Göttingen, and Hilbert was buried in relative obscurity, his funeral attended by fewer than dozen people and hardly reported in the press.
<< Back to Russell and Whitehead | Forward to Gödel >> |
