JUMP TO TOPIC
ARCHIMEDES OF SYRACUSE – Eureka & The Principle
Biography – Who was Archimedes
 |
Archimedes (c.287-212 BCE) |
Another Greek mathematician who studied at Alexandria in the 3rd Century BCE was Archimedes, although he was born, died and lived most of his life in Syracuse, Sicily (a Hellenic Greek colony in Magna Graecia). Little is known for sure of his life, and many of the stories and anecdotes about him were written long after his death by the historians of ancient Rome.
Also an engineer, inventor and astronomer, Archimedes was best known throughout most of history for his military innovations like his siege engines and mirrors to harness and focus the power of the sun, as well as levers, pulleys and pumps (including the famous screw pump known as Archimedes’ Screw, which is still used today in some parts of the world for irrigation).
But his true love was pure mathematics, and the discovery in 1906 of previously unknown works, referred to as the “Archimedes Palimpsest”, has provided new insights into how he obtained his mathematical results. Today, Archimedes is widely considered to have been one of the greatest mathematicians of antiquity, if not of all time, in the august company of mathematicians such as Newton and Gauss.
Method of Exhaustion
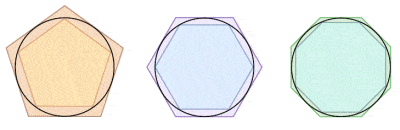 |
Approximation of the area of circle by Archimedes’ method of exhaustion |
Archimedes produced formulas to calculate the areas of regular shapes, using a revolutionary method of capturing new shapes by using shapes he already understood. For example, to estimate the area of a circle, he constructed a larger polygon outside the circle and a smaller one inside it. He first enclosed the circle in a triangle, then in a square, pentagon, hexagon, etc, etc, each time approximating the area of the circle more closely. By this so-called “method of exhaustion” (or simply “Archimedes’ Method”), he effectively homed in on a value for one of the most important numbers in all of mathematics, π. His estimate was between 31⁄7 (approximately 3.1429) and 310⁄71 (approximately 3.1408), which compares well with its actual value of approximately 3.1416.
Interestingly, Archimedes seemed quite aware that a range was all that could be established and that the actual value might never be known. His method for estimating π was taken to the extreme by Ludoph van Ceulen in the 16th Century, who used a polygon with an extraordinary 4,611,686,018,427,387,904 sides to arrive at a value of π correct to 35 digits. We now know that π is in fact an irrational number, whose value can never be known with complete accuracy.
Similarly, he calculated the approximate volume of a solid like a sphere by slicing it up into a series of cylinders, and adding up the volumes of the constituent cylinders. He saw that by making the slices ever thinner, his approximation became more and more exact, so that, in the limit, his approximation became an exact calculation. This use of infinitesimals, in a way similar to modern integral calculus, allowed him to give answers to problems to an arbitrary degree of accuracy, while specifying the limits within which the answer lay.
Quadrature of the Parabola
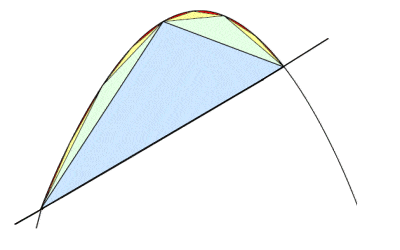 |
Archimedes’ quadrature of the parabola using his method of exhaustion |
Archimedes’ most sophisticated use of the method of exhaustion, which remained unsurpassed until the development of integral calculus in the 17th Century, was his proof – known as the Quadrature of the Parabola – that the area of a parabolic segment is 4⁄3 that of a certain inscribed triangle. He dissected the area of a parabolic segment (the region enclosed by a parabola and a line) into infinitely many triangles whose areas form a geometric progression. He then computed the sum of the resulting geometric series, and proved that this is the area of the parabolic segment.
In fact, Archimedes had perhaps the most prescient view of the concept of infinity of all the Greek mathematicians. Generally speaking, the Greeks’ preference for precise, rigorous proofs and their distrust of paradoxes meant that they completely avoided the concept of actual infinity. Even Euclid, in his proof of the infinitude of prime numbers, was careful to conclude that there are “more primes than any given finite number” i.e. a kind of “potential infinity” rather than the “actual infinity” of, for example, the number of points on a line. Archimedes, however, in the “Archimedes Palimpsest”, went further than any other Greek mathematician when, on compared two infinitely large sets, he noted that they had an equal number of members, thus for the first time considering actual infinity, a concept not seriously considered again until Georg Cantor in the 19th Century.
Another example of the meticulousness and precision of Archimedes’ work is his calculation of the value of the square root of 3 as lying between 265⁄153 (approximately 1.7320261) and 1351⁄780 (approximately 1.7320512) – the actual value is approximately 1.7320508. He even calculated the number of grains of sand required to fill the universe, using a system of counting based on the myriad (10,000) and myriad of myriads (100 million). His estimate was 8 vigintillion, or 8 x 1063.
 |
Archimedes showed that the volume and surface area of a sphere are two-thirds that of its circumscribing cylinder |
The discovery of which Archimedes claimed to be most proud was that of the relationship between a sphere and a circumscribing cylinder of the same height and diameter. He calculated the volume of a sphere as 4⁄3πr3, and that of a cylinder of the same height and diameter as 2πr3. The surface area was 4πr2 for the sphere, and 6πr2 for the cylinder (including its two bases). Therefore, it turns out that the sphere has a volume equal to two-thirds that of the cylinder, and a surface area also equal to two-thirds that of the cylinder. Archimedes was so pleased with this result that a sculpted sphere and cylinder were supposed to have been placed on his tomb of at his request.
The Archimedes Principle
Despite his important contributions to pure mathematics, though, Archimedes is probably best remembered for the anecdotal story of his discovery of a method for determining the volume of an object with an irregular shape.
Eureka! Eureka!
King Hieron of Syracuse had asked Archimedes to find out if the royal goldsmith had cheated him by putting silver in his new gold crown, but Archimedes clearly could not melt it down in order to measure it and establish its density, so he was forced to search for an alternative solution.
 |
An experiment to demonstrate Archimedes’ Principle |
While taking his bath on day, he noticed that that the level of the water in the tub rose as he got in, and he had the sudden inspiration that he could use this effect to determine the volume (and therefore the density) of the crown. In his excitement, he apparently rushed out of the bath and ran naked through the streets shouting, “Eureka! Eureka!” (“I found it! I found it!”). This gave rise to what has become known as Archimedes’ Principle: an object is immersed in a fluid is buoyed up by a force equal to the weight of the fluid displaced by the object.
Give me a place to stand on and I will move the Earth
Another well-known quotation attributed to Archimedes is: “Give me a place to stand on and I will move the Earth”, meaning that, if he had a fulcrum and a lever long enough, he could move the Earth by his own effort, and his work on centres of gravity was very important for future developments in mechanics.
According to legend, Archimedes was killed by a Roman soldier after the capture of the city of Syracuse. He was contemplating a mathematical diagram in the sand and enraged the soldier by refusing to go to meet the Roman general until he had finished working on the problem. His last words are supposed to have been “Do not disturb my circles!”
<< Back to Euclid | Forward to Diophantus >> |
