PLATO – THE ATHENIAN PHILOSOPHER
Biography: What was Plato Known for
 |
Plato (c.428-348 BCE) |
Although usually remembered today as a philosopher, Plato was also one of ancient Greece’s most important patrons of mathematics. Inspired by Pythagoras, he founded his Academy in Athens in 387 BCE, where he stressed mathematics as a way of understanding more about reality. In particular, he was convinced that geometry was the key to unlocking the secrets of the universe. The sign above the Academy entrance read: “Let no-one ignorant of geometry enter here”.
Plato played an important role in encouraging and inspiring Greek intellectuals to study mathematics as well as philosophy. His Academy taught mathematics as a branch of philosophy, as Pythagoras had done, and the first 10 years of the 15 year course at the Academy involved the study of science and mathematics, including plane and solid geometry, astronomy and harmonics. Plato became known as the “maker of mathematicians”, and his Academy boasted some of the most prominent mathematicians of the ancient world, including Eudoxus, Theaetetus and Archytas.
He demanded of his students accurate definitions, clearly stated assumptions, and logical deductive proof, and he insisted that geometric proofs be demonstrated with no aids other than a straight edge and a compass. Among the many mathematical problems Plato posed for his students’ investigation were the so-called Three Classical Problems (“squaring the circle”, “doubling the cube” and “trisecting the angle”) and to some extent these problems have become identified with Plato, although he was not the first to pose them.
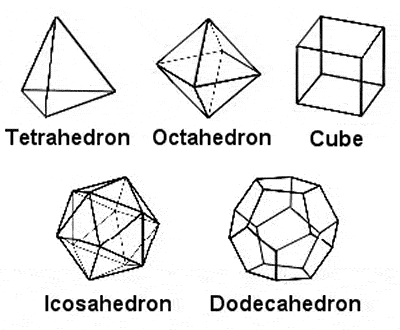
Platonic Solids
 |
Platonic Solids |
Plato the mathematician is perhaps best known for his identification of 5 regular symmetrical 3-dimensional shapes, which he maintained were the basis for the whole universe, and which have become known as the Platonic Solids: the tetrahedron (constructed of 4 regular triangles, and which for Plato represented fire), the octahedron (composed of 8 triangles, representing air), the icosahedron (composed of 20 triangles, and representing water), the cube (composed of 6 squares, and representing earth), and the dodecahedron (made up of 12 pentagons, which Plato obscurely described as “the god used for arranging the constellations on the whole heaven”).
The tetrahedron, cube and dodecahedron were probably familiar to Pythagoras, and the octahedron and icosahedron were probably discovered by Theaetetus, a contemporary of Plato. Furthermore, it fell to Euclid, half a century later, to prove that these were the only possible convex regular polyhedra. But they nevertheless became popularly known as the Platonic Solids, and inspired mathematicians and geometers for many centuries to come. For example, around 1600, the German astronomer Johannes Kepler devised an ingenious system of nested Platonic solids and spheres to approximate quite well the distances of the known planets from the Sun (although he was enough of a scientist to abandon his elegant model when it proved to be not accurate enough).
<< Back to Pythagoras | Forward to Hellenistic Mathematics >> |
