The Direction Of A Vector – Explanation and Examples

In the realm of vector geometry, the direction of a vector plays a fundamental role. The direction of  a vector  is defined as:

“The direction of a vector is the direction along which it acts.”

Keeping the importance of direction in mind, let’s move forward.   

We will be covering the following topics in this section:

• What is the direction of a vector?
• How to find the direction of a vector?
• What is the formula for finding the direction of a vector?
• Examples
• Practice problems 

What Is The Direction Of A Vector?

A vector is a physical quantity described by a magnitude and direction. A vector quantity is represented by a vector diagram and hence has a direction—the orientation at which the vector points is specified as the direction of a vector. 

In convention, where its vector diagram represents a vector, its direction is determined by the counterclockwise angle it makes with the positive x-axis. According to a scale, the vector diagram is a line with an arrowhead that denotes the direction of the vector. 

A = |A| Â

|A| represents magnitude, and  represents the unit vector.

For example, to describe a body’s velocity completely, we will have to mention its magnitude and direction. This means that we will have to mention how fast it is going in terms of distance covered per unit time and describe what direction it is headed. 

So, if we say a car is moving at 40 km/hr. This statement only describes the speed of the body. If someone says a car is moving at 40 km/hr and is headed North. This statement is describing the velocity of the car. It tells us the magnitude by which the car is moving and the direction in which it is headed.  

This is why, for us to describe a vector, the direction is just as vital and the magnitude. If we were to say that the chocolates are 3 meters outside of the classroom towards the North, it would make more sense. 

We have seen in the above-mentioned example how the direction is important to a vector quantity.

The arrowhead donates the direction of the vector, and the tail represents the point of action. There are two conventional ways to describe the direction of a vector.

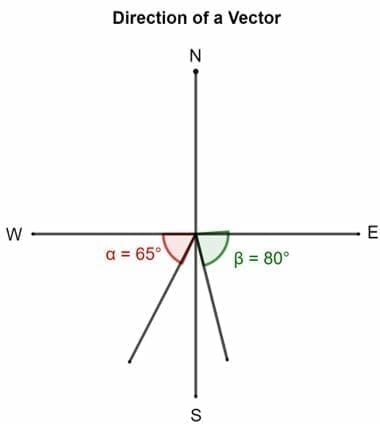
• A vector’s direction can be described by the angle its tail forms with East, North, West, or South. For instance, while describing a vector, it can be said that a vector is directed 80° South of East. This means that the vector has been rotated 80° from the East towards the South. The purple vector represents this. 

Similarly, another vector can be 65° South of the West. This means that it is directed 65° about the tail from the West toward the South. The green vector denotes this.

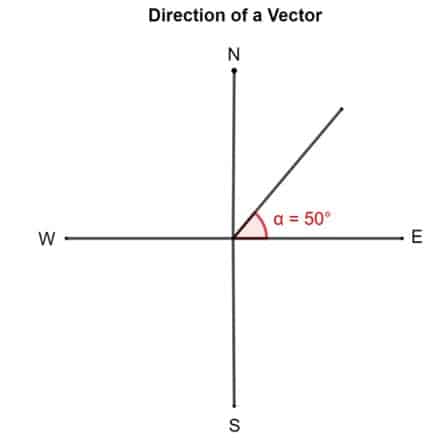
• Another way to describe a vector is by the counterclockwise angle of rotation from the due “East.” According to this, a vector with a direction of 50° is directed 50° from the East.

Let’s see this vector diagram. If a vector is said to have a direction of 50°. The trick to figuring it out is to pin down the tail of the vector aligned with the due East or the x-axis. Now rotate the vector 50° counterclockwise about its tail. 

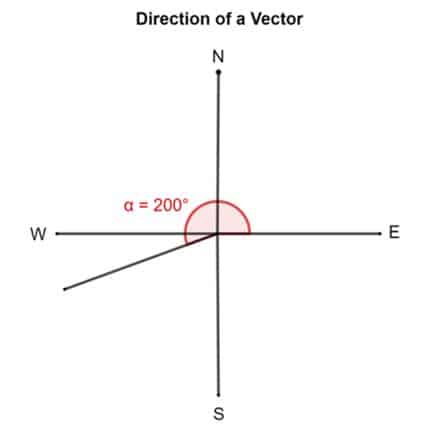
Now take another example. Suppose a vector has a direction of 200°. This means the vector’s tail is pinned down at the East and is then rotated 200° about counterclockwise.

Similarly, a Rectangular coordinate system can also be used. In that case, the angle will be calculated from the positive x-axis. 

Now, let’s consider some examples to understand this concept better. 

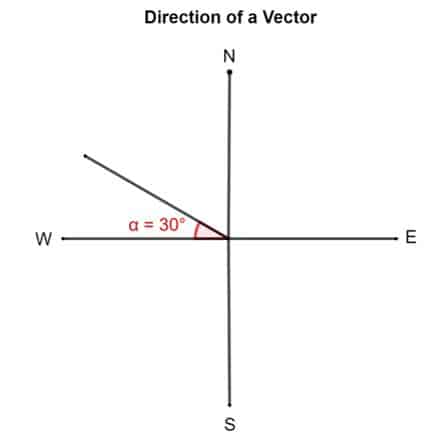
Example 1

Draw a vector 30° North of West. 

Solution

Example 2

Draw a vector with direction 60° East of North.

Solution

How To Find The Direction Of A Vector?

The direction of a vector is determined by the angle it makes with the horizontal line. 

There are two methods of finding the direction of a vector: 

1. Graphical Method
2. Using Inverse Tangent Formula

Graphical Method

The graphical method, as the name suggests, requires you to draw the vector graphically and then calculate the angle. The steps for the graphical method are as follows: 

1. Draw the individual vectors with their tails at origin and according to their angles. 
2. Using the head-to-tail rule, add the vectors. 
3. The resultant vector R is directed from the tail of the first vector A to the head of the second vector B. 
4. The magnitude and direction of the vector are then determined by using the ruler and protractor. The length of the resultant vector R will give it magnitude. 
5. For direction, draw a line parallel to the x-axis passing through the starting point of the resultant vector R. Measure the angle between the horizontal line and the resultant.

However, here is the problem: This method is only for basic understanding. It gets complicated if you have to add multiple vectors and does not always give the most accurate result. There is always a chance of human error. Therefore, we have the second method: 

The Inverse Tangent Formula 

We use the inverse tangent function to find the angle it makes with the horizontal line. 

This is possible if you have the initial and final coordinate points of a vector in a plane. It is given by:

θ = tan-1 (y/x)

Example 3

A vector is directed from origin to the (3,5). Determine its direction. 

Solution

Here we can see that, 

a = x = 3

b = y = 5

θ = tan-1 (a/b) 

θ = tan-1 (3/5)

θ = 30.9°

The vector is directed at 30.9° from the x-axis. 

Now, consider a case where the tail is not located at the origin, but rather the vector is placed somewhere else in the plane. In this case, the formula is modified as follows: 

By Pythagorean property, we know: 

tanθ = Δy/Δx

tanθ = (y2 – y1)/(x2 – x1)

θ = tan-1 (y2 – y1)/(x2 – x1)

So, the formula is modified as:

θ = tan-1 (y1 – y0)/(x1 – x0)

The angle given by this is from the horizontal line, running parallel to the x-axis. 

Let’s solve some examples to understand this concept. 

Example 4

Find the direction of the vector located from A(2,1) to B(6,9)

Δx = x1 – x0 = 6 -2 = 4

Δy = y1 – y0 = 9 -1 = 8

Solution

Using formula:

θ = tan-1 (y1 – y0)/(x1 – x0)

θ = tan-1 (8/4)

θ = 63.4°

The Conventions For The Direction Of A Vector

Let’s move on to a much tougher case. 

We have seen that in the above example, the vector lies in the First Quadrant. Let’s see how it works for the rest of the Quadrants. This can be determined by the signs of the vector’s coordinates, which determine the quadrant in which the angle lies. 

For this, certain conventions should be followed:

1. If both the coordinates are positive, then the angle exists in the first quadrant and is considered as the standard angle. θ = Ⲫ
2. If the y-coordinate is positive, but the x-coordinate is negative, then the angle exists in the 2nd quadrant then the standard angle is: θ = 180 + Ⲫ
3. If both the coordinates are negative, then the angle exists in the 3rd quadrant then the standard angle is: θ = 270 + Ⲫ
4. If the x-coordinate is positive, but the y-coordinate is negative, then the standard angle is: θ = 360 +  Ⲫ. 

Let’s under this with the help of examples.

Example 5

Find the direction of a vector directed from origin to the coordinates (6, -7). 

Solution

We will take help from the inverse tangent formula: 

θ = tan-1 (-7/6)

θ = -49.23°

Here we can see from the coordinates of the vector that it was lying in Quadrant IV. 

Now, here is the deal:

The formula gives the shortest angle from either the positive or negative x-axis. The convention is to represent the angle with a positive sign from the positive x-axis. For this, we subtract from 360 ° to the obtained angle. 

θ’ = -49.23 + 360

θ = 310.77°

Example 6

Find the direction of the vector (-4,3).

Solution

By looking at the coordinates, we know that the vector lies in Quadrant II:

θ = tan-1 (3/-4)

θ = -36.87°

This is the angle from the negative x-axis. Now, to get the positive answer, and calculated from the positive x-axis counterclockwise: 

θ = -36.87 + 180

θ = 143.13°

from the positive x-axis in a counter-clockwise direction. 

For Finding The Direction Of The Resultant Vector

Moving on, let’s see how we can find the direction of the resultant of two or more vectors. 

As you know, to calculate the resultant vector of two or more individual vectors, we find their respective rectangular coordinates first. Next, we add the x-component and y-component of the two vectors. The resultant x-component and y component are, in fact, the components of the resultant vector. 

Following are the step to calculate the direction of a resultant of two or more vectors: 

Let’s say you have vectors A and B, and you want to find their resultant and direction.

1. Dissolve both vectors into their rectangular components. 
2. We know, R = A + B. Similarly, Rₓ = Aₓ + Bₓ and R𝚢 = A𝚢 + B𝚢
3. Now using the inverse tangent property, replace x and y with x, y-components of the resultant, i.e., =tan-1(Ry/Rx)
4. Determine the quadrant of the resultant and modify theta according to it.

Practice Problems 

1. Find the direction of a vector whose initial and final points are (5, 2) and (4, 3), respectively. 
2. Find the direction of a vector whose initial and final points are (2, 3) and (5, 8), respectively. 
3. A vector is directed from the origin to (7, 4). Find its direction. 
4. Find the direction of a vector whose coordinates are (-7, -5).
5. Find the direction of a vector whose coordinates are (1, -1).

Answers

1. -45° or 135°
2. 59°
3. 29.74°
4. 234°
5. -45° or 135°

All the vector diagrams are constructed by using GeoGebra.

Previous Lesson | Main Page | Next Lesson