JUMP TO TOPIC
Square Root of 121 + Solution With Free Steps

The square root of 121 is indicated as √121, equal to 11. The number 121 is a perfect square. The square root of 121 in exponent form can be expressed as (121)$^1/2$. The power 1/2 is equivalent to 0.5.
In this article, we will analyze and find the square root of 121 using various mathematical techniques, such as the approximation method and the long division method.
What Is the Square Root Of 121?
The square root of the number 121 is 11.
The square root can be defined as the quantity that can be doubled to produce the square of that similar quantity. In simple words, it can be explained as:
√121 = √(11 x 11)
√121 = √(11)$^2$
√121 = ±11
The square can be canceled with the square root as it is equivalent to 1/2, therefore, obtaining 11. Hence y is 121’s square root. The square root generates both positive and negative integers.
How To Calculate the Square Root of 121?
You can calculate the square root of 121 using any of two vastly used techniques in mathematics; one is the Approximation technique, and the other is the Long Division method.
The symbol √ is interpreted as 121 raised to the power 1/2. So any number, when multiplied by itself, produces its square, and when the square root of any squared number is taken, it has the actual number.
Let us discuss each of them to understand the concepts better.
Square Root by Long Division Method
The process of long division is one of the most common methods used to find the square roots of a given number. It is easy to comprehend and provides more reliable and accurate answers. The long division method reduces a multi-digit number to its equal parts.
Learning how to find the square root of a number is easy with the long division method. All you need are five primary operations- divide, multiply, subtract, bring down or raise, then repeat.
Following are the simple steps that must be followed to find the square root of 121 using the long division method:
Step 1
First, write the given number 121 in the division symbol, as shown in figure 1.
Step 2
Starting from the right side of the number, divide the number 121 into pairs such as 21 and 1.
Step 3
Now divide the digit 1 by a number, giving a number either 1 or less than 1. Therefore, the remainder is zero in this case, whereas the quotient is one.
Step 4
After this, bring down the next pair, 21. Now the dividend is 21. To find the next divisor, we need to double our quotient obtained before. Doubling 1 gives 2; hence consider it as the next divisor.
Step 5
Now pair 2 with another number to make a new divisor that results in $\leq$ 21 when multiplied with the divisor. If the number is not a perfect square, add pair of zeros to the right of the number before starting division.
Step 6
Adding 1 to the divisor and multiplying 2 with 1 results in 21 = 21. The remainder obtained is 0. The long division process is shown below in figure 1:
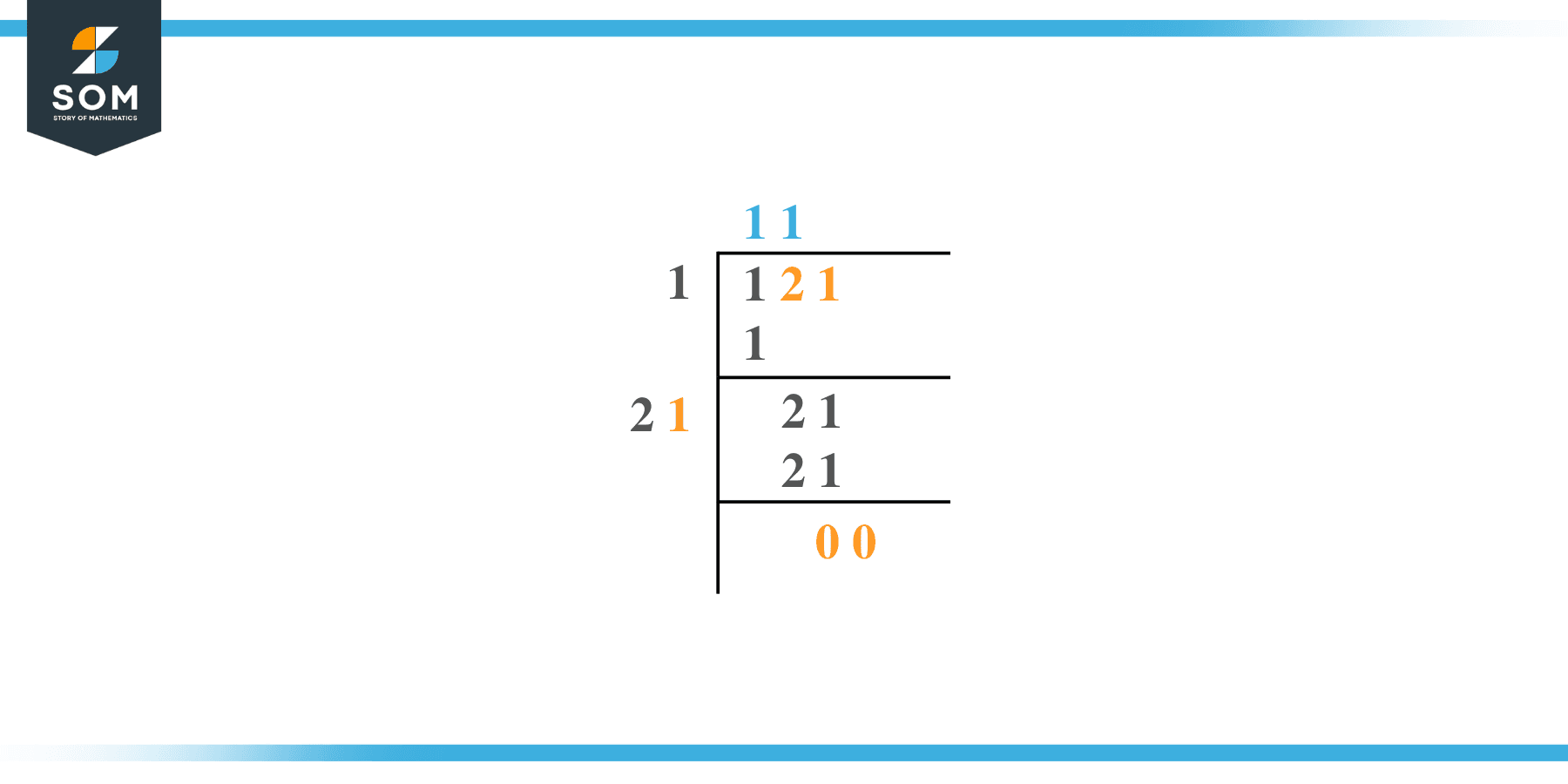
Important points
- The number 121 is a perfect square.
- The number 121 is rational.
- The number 121 can be split into its prime factorization.
Is Square Root of 121 a Perfect Square?
The number 121 is a perfect square. A number is a perfect square if it splits into two equal parts or identical whole numbers. If a number is a perfect square, it is also rational.
A number expressed in p/q form is called a rational number. All the natural numbers are rational. A square root of a perfect square is a whole number; therefore, a perfect square is a rational number.
A number that is not a perfect square is irrational as it is a decimal number. As far as 121 is concerned, it is a perfect square. It can be proved as below:
Factorization of 121 results in 11 x 11, which can also be expressed as a$^2$.
Taking the square root of the above expression gives:
= √(11$^2$)
= (11$^2$)$^{1/2}$
= 11
This shows that 121 is a perfect square and a rational number.
Therefore the above discussion proves that the square root of 121 is equivalent to 11.
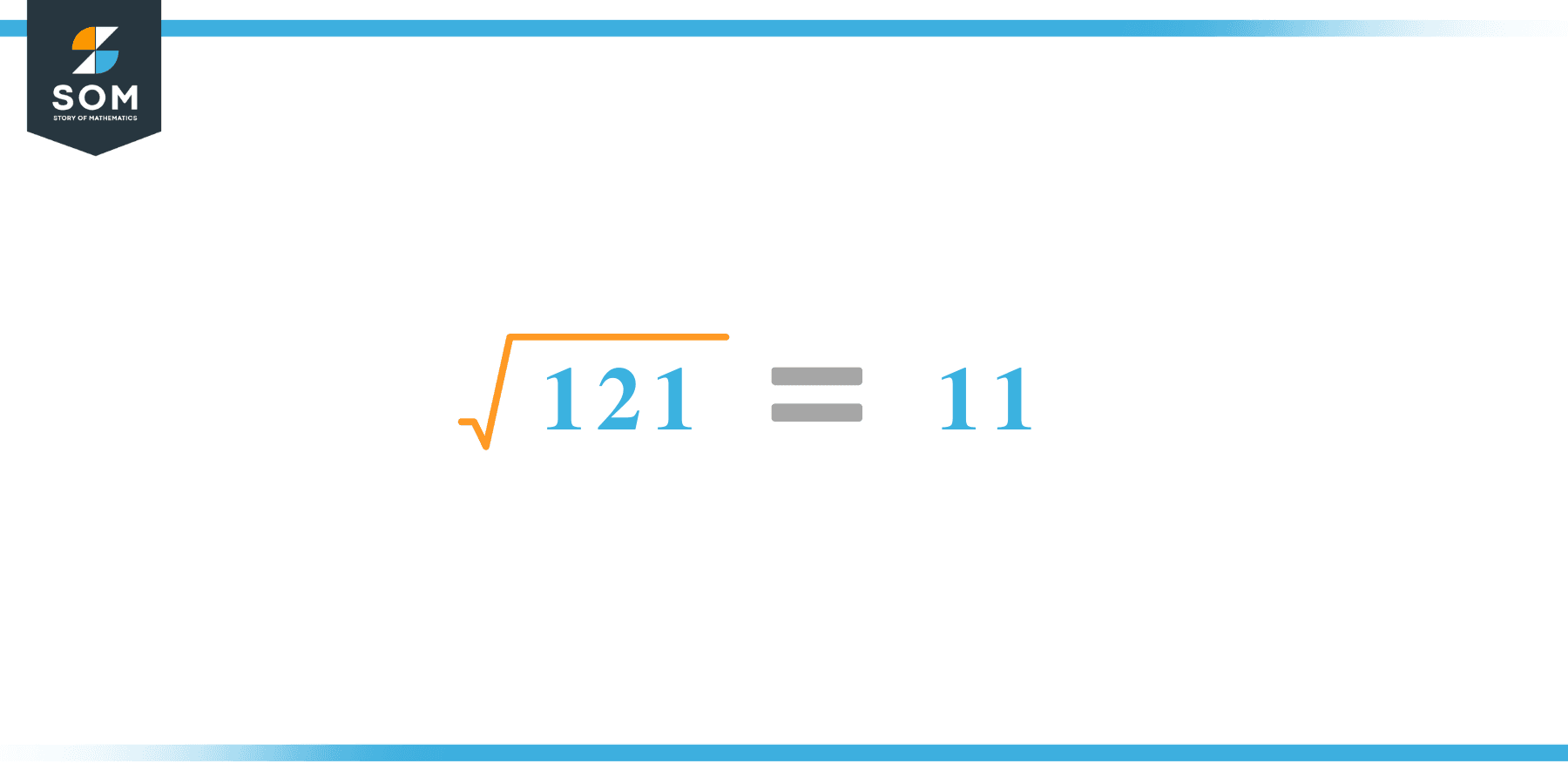
Images/mathematical drawings are created with GeoGebra.
