Squares & Square Roots – Difference & Examples

What is Square of a Number?

In mathematics, square of a number is the result of multiplying the number by itself. The word square is usually equivalent to raising a number to the power of 2 and denoted by the superscript 2.

For example, the square of 4 is written as 4² which gives 16 as the answer. In this case, 16 is the square of number 4.

Below is a list of squares of the first twelve numbers:

1 x 1 = 1                           7 x 7 = 49
2 x 2 = 4                           8 x 8 = 64
3 x 3 = 9                           9 x 9 = 81
4 x 4 = 16                        10 x 10 = 100
5 x 5 = 25                        11 x 11 = 121
6 x 6 = 36                        12 x 12 = 144

 

Squaring Negative Numbers

The square of a negative number is a positive number. For instance, -3 x -3 would become 9, however – 3 x 3 = -9, this is because -3 is a different number to 3.

What is Square Root of a Number?

The square root is an inverse operation of squaring a number. In other words, the square root is an operation that undoes an exponent of 2. A square root of a number x is such that a number y is the square of x, simplify written as y² = x.

For example, 5 and – 5 are both square roots of 25 because:

5 x 5 = 25 and -5 x -5 =25.

The square root of a number x is denoted with a radical sign √x or x ^1/2. For instance, the square root of 16 is represented as √16 = 4. A number whose square root is calculated is referred to as radicand. In this expression, √16 = 4, number 16 is the radicand.

Properties

• A perfect square number has a perfect square root.
• An even perfect number has the square root that is even.
• The odd perfect number has the square root that is odd.
• The square root of a negative number is undefined.
• Only numbers ending with an even number of zeros have square roots.

Finding the Square Root of Numbers

• Repeated Subtraction:
  This method involves successful and repeated subtraction of odd numbers such as 1, 3, 5, and 7 from the number until zero is reached. The square of the number is equal to the number or frequency of subtraction performed on the number. Suppose we need to calculate the square of a perfect number like 16, the number of subtractions performed is 4, so the square root of 16 is 4.
• Prime Factorization:
  In this method, a perfect square number is factorized by successive divisions. The prime factors are grouped into pairs, and the product of each number is calculated. The product is therefore, the square root of the number. To find the square of a perfect number such as: 144 is performed as:

1. 144 = 2 × 2 × 2 × 2 × 3 × 3.
2. Pair the prime factors.
3. Selecting one number from each pair.
4. 2 × 2 × 3 = 12.
5. Thus, the √144 = 12.

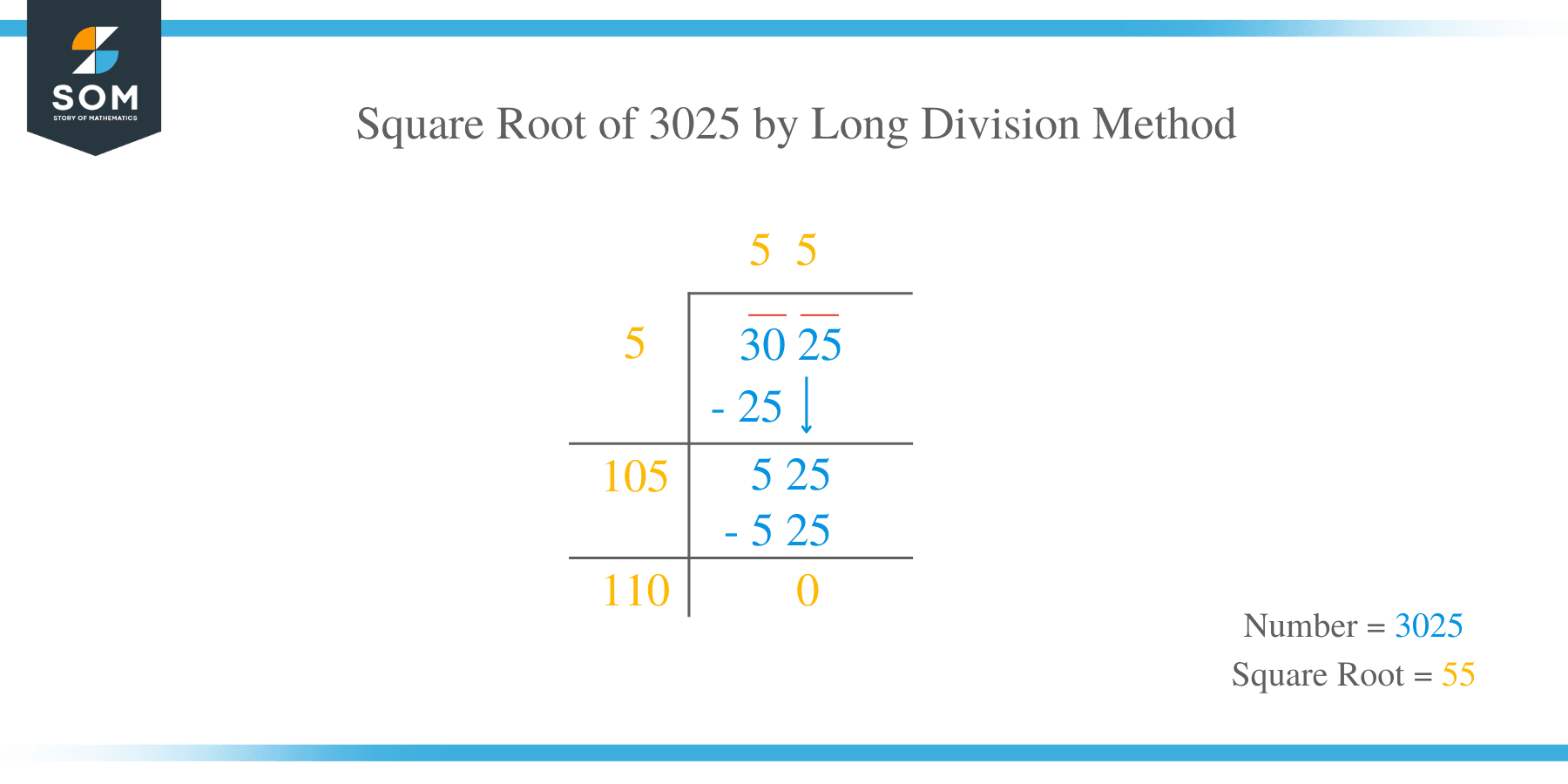
• Division Method:
  Division method is a suitable technique of calculating the square of a large number.
  
  The following are the steps involved:

1. A bar is placed over every pair of digits starting from the right-hand side.
2. Divide left end number by a number whose square is less or equivalent to the numbers under the left end.
3. Take this number as the divisor and quotient. Similarly, take the leftmost number as the dividend.
4. Divide to get the result.
5. Pull down the next number with a bar to the right-hand side of the remainder.
6. Multiply the divisor by 2.
7. To the right of this new divisor, find a suitable dividend. This process is repeated until we get zero as the remainder. The square of the number therefore is equal to the quotient.