JUMP TO TOPIC
What Is the Percentage Difference From 1000 To 200 + Solution with Free Steps

The percentage difference from 1000 to 200 is equivalent to -400%. This solution may be calculated by multiplying the difference between 200 and 1000 (i.e. 200 – 1000 ) by 100 and then dividing the result by 1000.
Such a calculation can be used in scenarios where one wants to keep track of the increases or decreases in some quantity in terms of percentage. Consider a business’s revenue, for example. Now let us say that the revenue of a business in a particular year jumps from 100 million dollars to 150 million dollars and you want to gauge the difference. You can simply calculate the percentage difference, which comes out to be 50%. So you can say that there has been a 50% growth in the revenue year on year.
What Is the percentage difference from 1000 to 200?
The percentage difference from 1000 to 200 equals -80%. This answer is obtained through the multiplication of the difference 200 – 1000 by 100 and further division by 1000.
The same solution can also be obtained by multiplying only 200 with 100 and then dividing it with 1000. Once we have this result, we subtract it from 100 to obtain the percentage difference.
How To Calculate percentage difference from 1000 to 200?
You can find the percentage difference from 1000 to 200 by some simple mathematical steps explained below.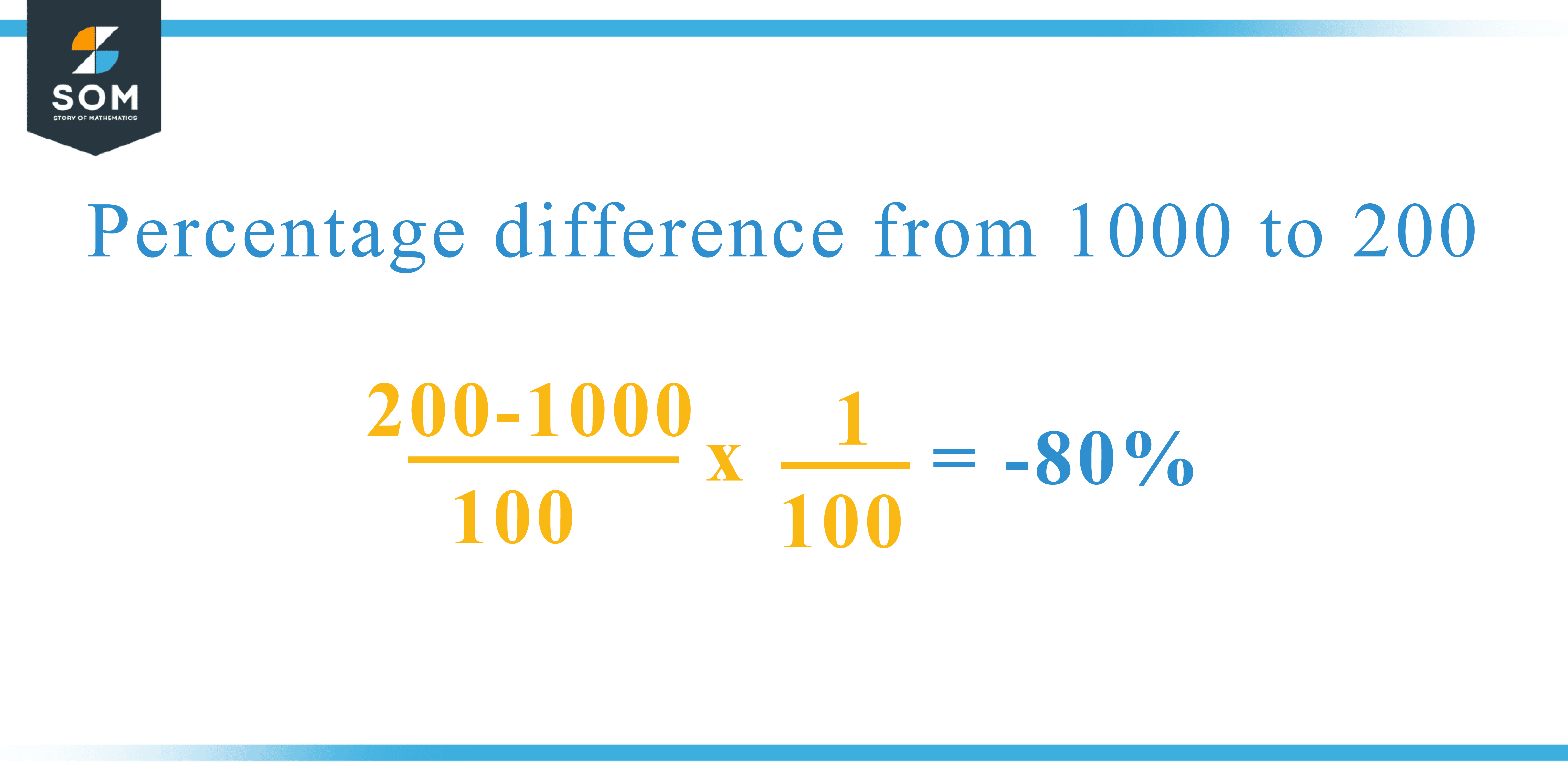
Step 1
Firstly, we find the difference of 1000 and 200:
Difference of 1000 and 200 = 200 – 1000 = – 800
Step 2
Lets find the percentage difference of 1000 and 200:
Percentage difference of 1000 and 200 = ( – 800 ) / [ 1000 ( 100 / 100 ) ]
Step 3
Deploying the arithmetic simplification process:
Percentage difference of 1000 and 200 = – 800 / 1000 x 1 / 100
Since, 1/100 is equal to the %:
Percentage difference of 1000 and 200 = -80%
This percentage difference can be represented on a pie chart for visualization. Let us suppose that the whole pie chart represents the 1000 value. Now, we find 80 percent of 1000, which is 800. The area occupied by the 800 value will represent the 80 percent of the total 1000 value. The remaining region of the pie chart will represent 20 percent of the total 1000 value. The 100% of 1000 will cover the whole pie chart as 1000 is the total value.
Any given number or quantity can be represented in percentages to better understand the total quantity. The percentage can be considered a quantity that divides any number into hundred equal parts for better representation of large numbers and understanding.
Percentage scaling or normalization is a very simple and convenient method of representing numbers in relative terms. Such notations find wide application in many industrial sectors where the relative proportions are used.
