JUMP TO TOPIC
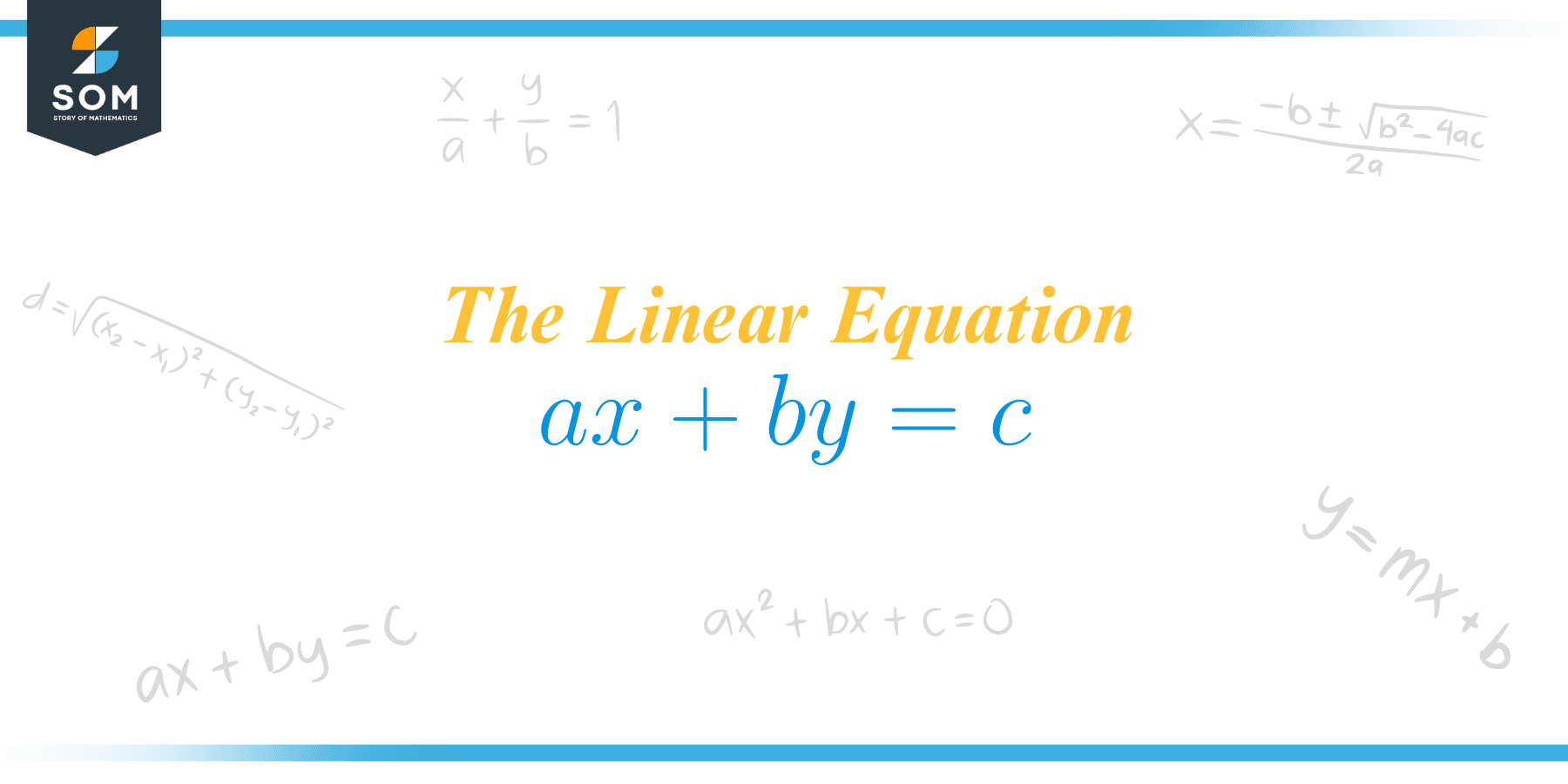$ax+by=c$ is the standard form for linear equations in two variables. It is relatively simple to find both intercepts when an equation is provided in this form, that is $x$ and $y$. This type is also beneficial for resolving two linear equation systems.
This complete guide will provide a detailed examination of the standard form, the slope-intercept form, and the point-slope form of the equation of the line along with methods to solve the linear equation in one and two variables.
What Is a Linear Equation $ax+by=c$?
A linear equation $ax+by=c$ is an algebraic expression in which every term has an exponent of one and produces a straight line when you plot it on a graph. This is the reason it is referred to as a linear equation. Two common types of linear equations are linear equations in one variable and linear equations in two variables.
More Information
A linear equation is an equation where the variable’s highest power is always $1$. A one-degree equation is another name for this. A linear equation in only one variable has the basic form $ax + b = 0$.
In this equation, $x$ is regarded as a variable, $a$ is a coefficient of $x$, and $b$ is a constant. A linear equation in two variables has the basic form $ax + by = c$. Here, $x$ and $y$ are regarded as variables, $a$ and $b$ are the coefficients of $x$ and $y$, and $c$ is the constant.
Linear Equations in One and Two Variables
The standard or common type of one-variable linear equations is regarded as $ax + b = 0$, in which $a$ and $b$ are real numbers and $x$ is the only variable.
A linear equation graph in one variable i.e. $x$ results in a vertical line parallel to the $y-$axis, while a linear equation graph in two variables $x$ and $y$ results in a straight line. A linear equation is expressed using the linear equation formula. This can be achieved in a number of forms. A linear equation, for instance, can be written in the standard form, the slope-intercept form, or the point-slope form.
Solving a Linear Equation in One Variable
An equation is equal to a weighing scale with the same weights on both sides. It always remains true if you subtract or add the same number from both sides of an equation. Likewise, it is valid to divide or multiply the same number on both sides of an equation. You can move the variables to one side of the equation and the constant to the other side, and afterward, we calculate the value of the undetermined variable. This is how you solve a linear equation with a single variable.
A linear equation with one variable is very simple to solve. To obtain the value of the unknown variable, the variables are separated and brought to one side of the equation, while the constants are combined and taken to the opposite side of the equation.
Example
To find the solution to the linear equation $2x+1=7$, place the numbers on the right side of the equation and keep the variable on the left side. It now becomes $2x = 7-1$. So when you solve for $x$, you will get $2x = 6$. In the end, you will have the value of $x$ as $x = 6/2 = 3$.
Solving a Linear Equation in Two Variables
A linear equation in two variables has the form $ax + by + c = 0$, where $a,b,$ and $c$ are regarded as real numbers with $x$ and $y$ being variables having the degrees of one. When two such linear equations are considered, they are referred to as simultaneous linear equations.
The substitution technique, graphical technique, cross multiplication technique, and elimination technique are all methods for solving linear equations in two variables.
Graphical Method
The basic method for solving linear equations graphically is to demonstrate them as straight lines on a graph and locate the intersection points if there are any. If you take the pair of two linear equations, you can conveniently determine at least two solutions by replacing the values for $x$, finding the $x$ and $y$ intercepts, and plotting these geometrically on the graph.
Continue to the following sections to see the types of solutions we can get by using the Graphical Method.
Unique Solution
You can regard the pair of equations as consistent if the point of intersection of two lines is the same and that point provides a solution to the equations which is unique.
Infinitely Many Solutions
If the two lines coincide, the pair of equations is considered to be dependent, and there are infinitely many solutions. Each point along a line will become a solution.
No Solution
If the two lines are parallel, the pair of equations is called inconsistent, and no solution will exist in this case.
Method of Substitution
The substitution technique is one of the algebraic approaches to solving a system of linear equations in two variables. In this approach, you determine the value of every variable by separating it on one side of the equation and getting every remaining term on the opposite side.
Then we plug that value into the second equation. It consists of simple steps for finding the values of variables in a system of linear equations using the substitution method.
Method of Cross Multiplication
In solving linear equations with two variables, the cross multiplication technique is utilized. This technique is the most simple approach to resolving linear equations in two variables. This technique is most commonly utilized in linear equations with two variables.
The cross multiplication formula is:
$\dfrac{x}{b_1c_1-b_2c_1}=\dfrac{-y}{a_1c_2-a_2c_1}=\dfrac{1}{a_1b_2-a_2b_1}$
Method of Elimination
By utilizing basic arithmetic operations, you can eliminate one of the given variables and afterward simplify the equation to determine the value of the second variable. Next, you can substitute that value into any of the equations to find the value of the variable that has been eliminated.
The solution/root of the linear equation is the value of the variable which satisfies the linear equation. The addition, subtraction, multiplication, or division of a number on both sides of the equation do not affect the equation. A linear equation with one or two variables always has a straight line as its graph.
What Is a Slope?
The slope or gradient of a line in mathematics refers to a number that represents both the orientation and the steepness of the line. The slope is the finest way to determine if the lines are perpendicular, parallel, or at any angle without employing any geometrical tool.
What Are the Types of Linear Equations?
The standard form, the slope-intercept form, and the point-slope form are the three types of linear equations. The standard form, $ax+by=c$, has already been discussed. Let’s take a look at the point-slope form and the slope-intercept form.
The Slope-Intercept Form
The slope-intercept form of linear equations is the usual one, and it is expressed as $y=mx+b$. Here, $m$ is the line’s slope and $b$ is the $y-$intercept. Also, $x$ and $y$ can be regarded as the $x$ and $y-$axis coordinates, respectively.
The Point-Slope Form
A straight line equation is found in this type of linear equation by taking the points in the $xy-$ plane such that: $y-y_1=m(x-x_1)$, where $(x_1, y_1)$ are the coordinates of the point. It may also be written as $y = mx + y_1 – mx_1$.
Intercept Form of the Equation of Line
The intercept form of a line equation is $x/a + y/b = 1$. This is among the most important types of line equations. In addition, the sign of the intercepts in the above equation tells us where the line is in relation to the coordinate axes.
The intercept form of the line equation is defined as the line that forms a right triangle with the coordinate axes, with the sides of lengths denoted as $a$ and $b$ units, respectively.
Conclusion
We’ve discussed a lot in terms of linear equations, their various forms, and the methods used to solve them. To have a greater and more thorough understanding of the concepts presented, let us summarize the entire study in this bullet list:
- The equation $ax+by=c$ is a linear equation in two variables.
- A linear equation is one where the variable’s highest power is always $1$.
- You will get one of the three basic types of solutions when you use the graphical method to solve the linear equation in two variables.
- A line’s slope or gradient is a number that indicates both its direction and its steepness.
- There are three basic types of linear equations, namely standard form, slope-intercept form, and the point-slope form.
The linear equation in a single variable can be solved while the equation in two variables requires some techniques for their solution, so the best practice is to take a few more examples with different values of $a,b$, and $c$ in $ax+by=c$ and apply the techniques to find their solutions. This will make you an expert in plotting and determining the solutions to linear equations.