JUMP TO TOPIC
The angle bisector theorem highlights the relationship shared between the line segments and sides of a given triangle. Since this theorem applies to all types of triangles, this opens a wide range of word problems, theorems and other applications in geometry.The angle bisector theorem shows how the line segments formed by the angle bisector and the sides of the triangle are proportional to each other. Thanks to triangle theorems like this, we can study how smaller triangles within a larger triangle behave. Learn the basics of the angle bisector theorem, understand its origin, and feel confident when applying the theorem!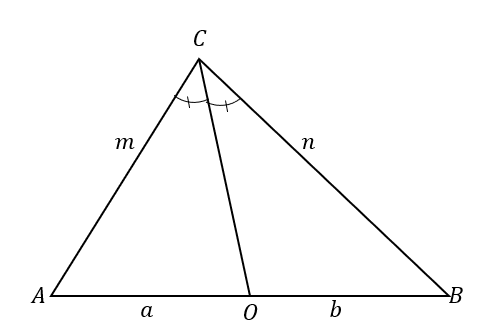
To better understand the angle bisector theorem, take a look at $\Delta ABC$. The angle bisector, $\overline{CO}$, divides $\angle ACB$ into two congruent angles.This also results in dividing the opposite side into two line segments: $\overline{AB}$. According to the angle bisector theorem, the ratios of the line segments $\overline{AO}$ and $\overline{OB}$ and the triangle’s sides $\overline{AC}$ and $\overline{BC}$ are proportional.\begin{aligned}\color{DarkOrange}\textbf{Angle Bisec} &\color{DarkOrange}\textbf{tor Theorem}\\\dfrac{\overline{AC}}{\overline{AO}} &=\dfrac{\overline{BC}}{\overline{BO}}\\\dfrac{m}{a} &=\dfrac{n}{b}\end{aligned}Let’s extend our understanding of the angle bisector theorem by applying what we’ve learned to analyze the triangle shown below. The line segment $\overline{CO}$ divides the angle $\angle ACB$ into two congruent angles, $\angle ACO =\angle OCB =40^{\circ}$. This means that $\overline{CO}$ is the angle bisector of the angle $\angle ACB$. The same line segment divides the opposite side, $\overline{AB}$, into two line segments.
The angle bisector theorem states that when this happens, the affected line segments and the two sides of the triangle are proportional.\begin{aligned}\dfrac{AC}{AO} &= \dfrac{BC}{BO}\\\dfrac{24}{18} &= \dfrac{16}{12}\\\dfrac{4}{3} &\overset{\checkmark}{=} \dfrac{4}{3}\end{aligned}This example highlights the important components needed to apply the angle bisector theorem. It’s now time to understand how this theorem was established to know it by heart.
We’ve established that $\overline{CO}$ bisects $\angle ACB$, so we have $\angle ACO = \angle OCB$ or $\angle 1 = \angle 2$. Since $\overline{CO}$ is parallel to $\overline{BP}$, we can relate $\angle 1$ and $\angle 3$ as well as $\angle 2$ and $\angle 4$:
Using the side splitter theorem, the line segments share the following proportionality:\begin{aligned}\dfrac{AO}{OB} &= \dfrac{AC}{CP}\end{aligned}Since $\angle 3 = \angle 4$, the triangle $\Delta CBP$ is isosceles and consequently, $\overline{CP} = \overline{CB}$. Substitute $\overline {CP}$ with $\overline{CB}$ and have the following relationship instead:\begin{aligned}\dfrac{AO}{OB} &= \dfrac{AC}{CB}\\ \dfrac{AC}{AO} &= \dfrac{CB}{OB}\end{aligned}This proves that when the angle bisector divides the third side into two line segments, the sides and the resulting line segments are proportional to each other.Now that we’ve proven the angle bisector theorem, it’s time to learn how to apply this theorem to solve different problems involving angle bisectors.
The converse statement establishes that when:
To confirm that the line $\overline{CO}$ is the angle bisector of $\angle ACB$, take a look at the ratios of the following line segments and sides of the triangle: $\overline{AC}$ and $\overline{AO}$ as well as $\overline{CB}$ and $\overline{OB}$.
Using the converse of the angle bisector theorem, the line segment $\overline{CO}$ is indeed the angle bisector of $\angle ACB$.Excited to try out more problems? Don’t worry, the section below offers more exercises and practice problems!
Since $\overline{MO}$ bisects $\angle LMN$ into two congruent angles and using the angle bisector theorem, the ratios of the sides are as follows:\begin{aligned}\dfrac{LM}{LO} &= \dfrac{MN}{ON}\\\dfrac{20}{15} &= \dfrac{24}{x}\end{aligned}Simplify the equation then solve $x$ to find the measure of the line segment $\overline{ON}$.\begin{aligned}\dfrac{4}{3} &= \dfrac{24}{x}\\4x&= 24(3)\\4x&= 72\\ x&= 18\end{aligned}This means that $\overline{ON}$ has a length of $18$ cm.
Using the angle bisector theorem, the ratio of $\overline{AC}$ and $\overline{AP}$ is equal to $\overline{CB}$ and $\overline{PB}$.\begin{aligned}\dfrac{AC}{AP} &= \dfrac{CB}{PB}\\\dfrac{36}{26- x} &= \dfrac{42}{x}\end{aligned}Apply cross-multiplication to simplify and solve the resulting equation. Find the length of $\overline{PB}$ by finding the value of $x$.\begin{aligned}36x &= 42(26- x)\\36x &= 1092- 42x\\36x + 42x &= 1092\\78x &= 1092\\x&= 14\end{aligned}Hence, the length of $\overline{PB}$ is equal to $14$ ft.
What Is the Angle Bisector Theorem?
The angle bisector theorem is a theorem stating that when an angle bisector bisects a triangle’s interior angle and divides the angle’s opposite side into two line segments, the following ratios are equal: each of the sides includes the angle being bisected and over the length of the adjacent line segment of the opposite side.To better understand the angle bisector theorem, take a look at $\Delta ABC$. The angle bisector, $\overline{CO}$, divides $\angle ACB$ into two congruent angles.This also results in dividing the opposite side into two line segments: $\overline{AB}$. According to the angle bisector theorem, the ratios of the line segments $\overline{AO}$ and $\overline{OB}$ and the triangle’s sides $\overline{AC}$ and $\overline{BC}$ are proportional.\begin{aligned}\color{DarkOrange}\textbf{Angle Bisec} &\color{DarkOrange}\textbf{tor Theorem}\\\dfrac{\overline{AC}}{\overline{AO}} &=\dfrac{\overline{BC}}{\overline{BO}}\\\dfrac{m}{a} &=\dfrac{n}{b}\end{aligned}Let’s extend our understanding of the angle bisector theorem by applying what we’ve learned to analyze the triangle shown below. The line segment $\overline{CO}$ divides the angle $\angle ACB$ into two congruent angles, $\angle ACO =\angle OCB =40^{\circ}$. This means that $\overline{CO}$ is the angle bisector of the angle $\angle ACB$. The same line segment divides the opposite side, $\overline{AB}$, into two line segments.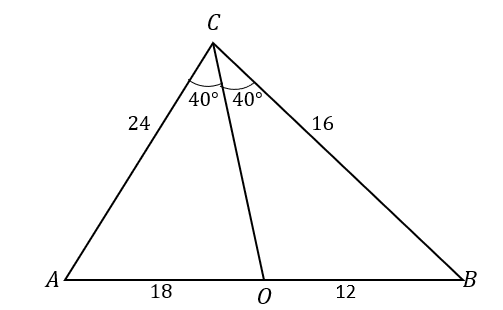
The angle bisector theorem states that when this happens, the affected line segments and the two sides of the triangle are proportional.\begin{aligned}\dfrac{AC}{AO} &= \dfrac{BC}{BO}\\\dfrac{24}{18} &= \dfrac{16}{12}\\\dfrac{4}{3} &\overset{\checkmark}{=} \dfrac{4}{3}\end{aligned}This example highlights the important components needed to apply the angle bisector theorem. It’s now time to understand how this theorem was established to know it by heart.Proving the Angle Bisector Theorem
When proving the angle bisector theorem, use the properties of parallel lines and the side splitter theorem. Begin the setup by extending the side of the triangle then constructing a line that’s parallel to the given angle bisector. These two new lines should meet and form an adjacent triangle.Take a look at the triangle $\Delta ABC$. It has an angle bisector, $\overline{CO}$, dividing $\angle ACB$ into two congruent angles. Extend $AC$ to form the line segment $\overline{AP}$ and construct a line parallel to $\overline{CO}$ that meets at $P$.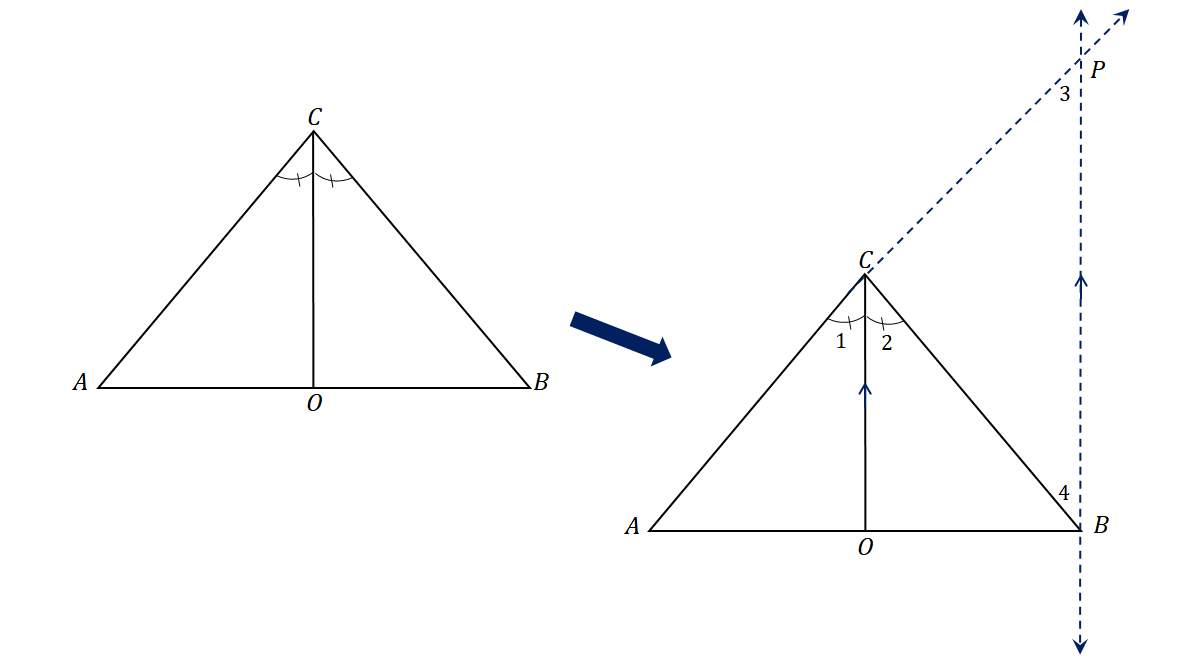
We’ve established that $\overline{CO}$ bisects $\angle ACB$, so we have $\angle ACO = \angle OCB$ or $\angle 1 = \angle 2$. Since $\overline{CO}$ is parallel to $\overline{BP}$, we can relate $\angle 1$ and $\angle 3$ as well as $\angle 2$ and $\angle 4$:- The angles $\angle 1$ and $\angle 3$ are corresponding angles, so $\angle 1 = \angle 3$.
- Similarly, since the angles $\angle 2$ and $\angle 4$ are alternate interior angles, $\angle 2 = \angle 4$.
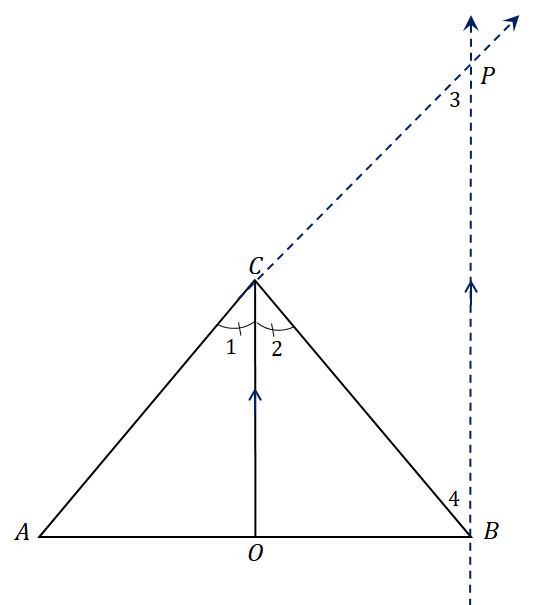Using the side splitter theorem, the line segments share the following proportionality:\begin{aligned}\dfrac{AO}{OB} &= \dfrac{AC}{CP}\end{aligned}Since $\angle 3 = \angle 4$, the triangle $\Delta CBP$ is isosceles and consequently, $\overline{CP} = \overline{CB}$. Substitute $\overline {CP}$ with $\overline{CB}$ and have the following relationship instead:\begin{aligned}\dfrac{AO}{OB} &= \dfrac{AC}{CB}\\ \dfrac{AC}{AO} &= \dfrac{CB}{OB}\end{aligned}This proves that when the angle bisector divides the third side into two line segments, the sides and the resulting line segments are proportional to each other.Now that we’ve proven the angle bisector theorem, it’s time to learn how to apply this theorem to solve different problems involving angle bisectors.How To Find the Angle Bisector?
To find the angle bisector of a triangle, apply the converse of the angle bisector theorem by observing the proportions of the pairs of sides to confirm that the given line segment is an angle bisector.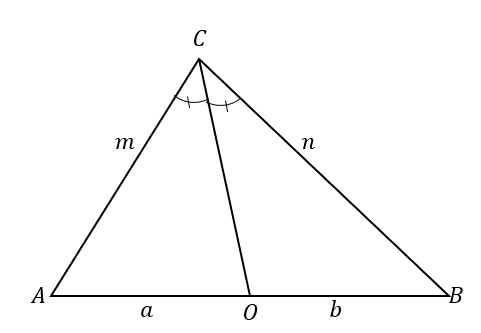
The converse statement establishes that when:- The line segment divides a vertex and angle of a triangle.
- It also divides the triangle into smaller triangles with proportional sides.
- The line segment is the angle bisector of the triangle.
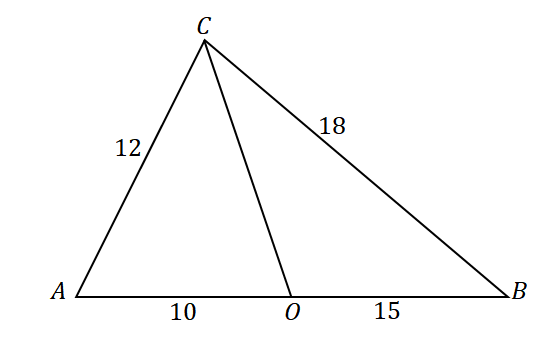To confirm that the line $\overline{CO}$ is the angle bisector of $\angle ACB$, take a look at the ratios of the following line segments and sides of the triangle: $\overline{AC}$ and $\overline{AO}$ as well as $\overline{CB}$ and $\overline{OB}$.| \begin{aligned}\dfrac{AC}{AO} &= \dfrac{12}{10}\\&= \dfrac{6}{5}\end{aligned} | \begin{aligned}\dfrac{CB}{OB}&= \dfrac{18}{15}\\&=\dfrac{6}{5}\end{aligned} |
| \begin{aligned}\dfrac{AC}{AO} &= \dfrac{CB}{OB}\\\Rightarrow \overline{CO}&: \text{Angle Bisector}\end{aligned} | |
Example 1
In the triangle $\Delta LMN$ the line $\overline{MO}$ bisects $\angle LMO$. Suppose that $\overline{LM} = 20$ cm, $\overline{MN} = 24$ cm, and $\overline{LO} = 15$ cm, what is the length of line segment $\overline{ON}$?Solution
First, construct a triangle with an angle bisector dividing the angle’s opposite side. Assign the given lengths of the triangle’s sides and the line segment $\overline{LO}$ as shown below. Let $x$ represent the measure of $\overline{ON}$.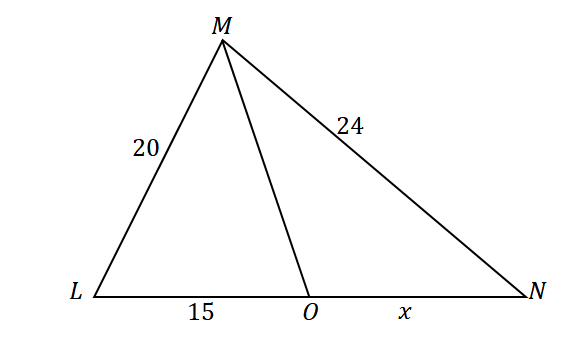
Since $\overline{MO}$ bisects $\angle LMN$ into two congruent angles and using the angle bisector theorem, the ratios of the sides are as follows:\begin{aligned}\dfrac{LM}{LO} &= \dfrac{MN}{ON}\\\dfrac{20}{15} &= \dfrac{24}{x}\end{aligned}Simplify the equation then solve $x$ to find the measure of the line segment $\overline{ON}$.\begin{aligned}\dfrac{4}{3} &= \dfrac{24}{x}\\4x&= 24(3)\\4x&= 72\\ x&= 18\end{aligned}This means that $\overline{ON}$ has a length of $18$ cm.Example 2
In the triangle $\Delta ACB$, the line $\overline{CP}$ bisects $\angle ACB$. Suppose that $\overline{AC} = 36$ ft, $\overline{CB} = 42$ ft, and $\overline{AB} = 26$ ft, what is the length of line segment $\overline{PB}$?Solution
Begin by constructing $\Delta ACB$ with the given components. Keep in mind that $\overline{CP}$ divides the opposite side $\overline{AB}$ into two line segments: $\overline{AP}$ and $\overline{PB}$. If $x$ represents the length of $\overline{PB}$, $\overline{AP}$ is equal to $(26 – x)$ ft.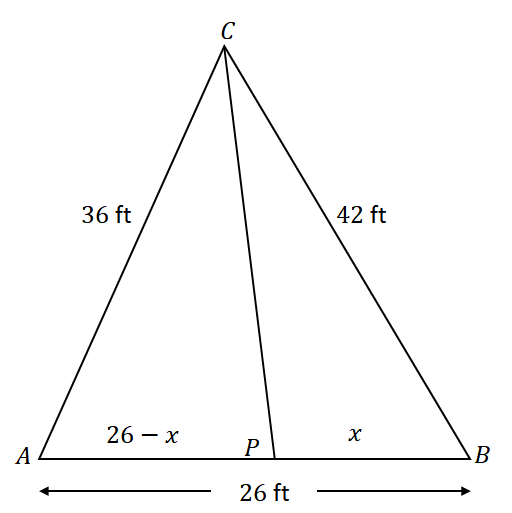
Using the angle bisector theorem, the ratio of $\overline{AC}$ and $\overline{AP}$ is equal to $\overline{CB}$ and $\overline{PB}$.\begin{aligned}\dfrac{AC}{AP} &= \dfrac{CB}{PB}\\\dfrac{36}{26- x} &= \dfrac{42}{x}\end{aligned}Apply cross-multiplication to simplify and solve the resulting equation. Find the length of $\overline{PB}$ by finding the value of $x$.\begin{aligned}36x &= 42(26- x)\\36x &= 1092- 42x\\36x + 42x &= 1092\\78x &= 1092\\x&= 14\end{aligned}Hence, the length of $\overline{PB}$ is equal to $14$ ft.