JUMP TO TOPIC
The phrase “closed under addition” is often mentioned when studying the properties and characteristics of different types of numbers. The closure property of addition highlights a special characteristic in rational numbers (among other groups of numbers). Knowing which set of numbers are closed under addition will also help in predicting the nature of complex quantities’ sums.
When a set of numbers or quantities are closed under addition, their sum will always come from the same set of numbers. Use counterexamples to disprove the closure property of numbers as well.
This article covers the foundation of closure property for addition and aims to make you feel confident when identifying a group of numbers that are closed under addition, as well as knowing how to spot a group of numbers that are not closed under addition.
There are a lot of exercises in this discussion to help you understand the addition’s closure property!
What Does Closed Under Addition Mean?
Closed under addition means that the quantities being added satisfy the closure property of addition, which states that the sum of two or more members of the set will always be a member of the set. Whole numbers, for example, are closed under addition.
This means that when two whole numbers are added, the resulting sum is also a whole number.
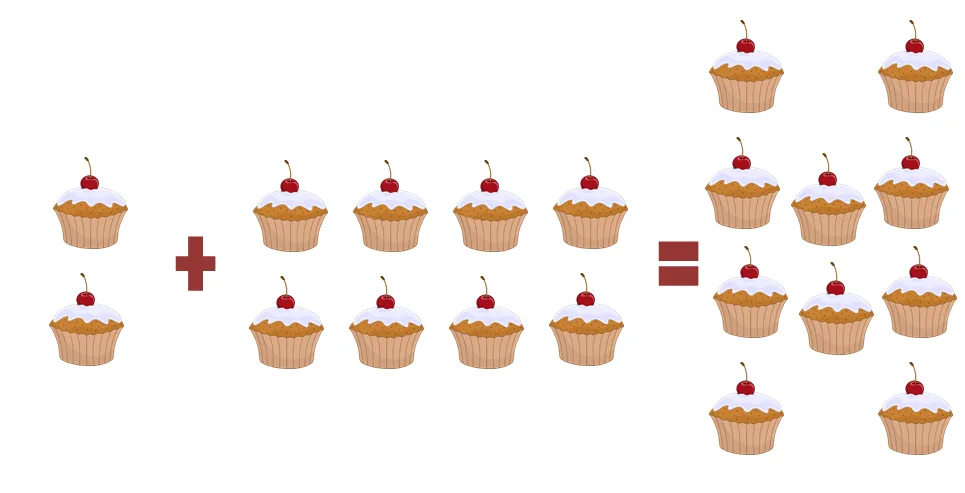
Take a look at the illustration shown above to better understand the concept of closed under addition. When two cupcakes are added to eight other cupcakes, what’s expected is that there will be ten cupcakes. It doesn’t make sense that the resulting combination will return nine cupcakes and a pie.
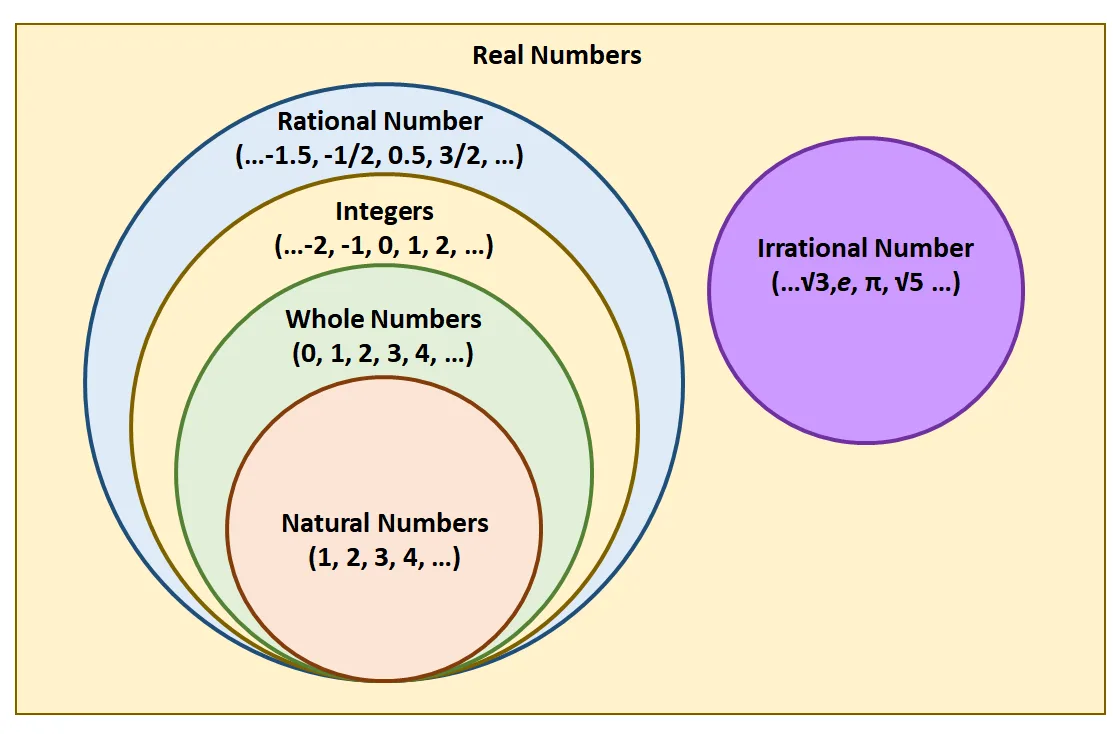
Extend this to a set of numbers and expressions that satisfy the closure property. When a group of quantities or set members are said to be closed under addition, their sum will always return a fellow set member. Take a look at the different sets (and subsets) of real numbers:
- Irrational numbers are all real numbers that can’t be written as a ratio of two integers.
- Rational numbers are those that can be written as a ratio of two integers.
- Integers are positive and negative whole numbers.
- Whole numbers are natural or counting numbers plus zero.
- Of course, natural numbers are the numbers we use for counting.
In general, all rational numbers are closed under addition. This means that adding a combination of these types of numbers will return real numbers as well. In addition, each subset of numbers is also closed under addition.
Here are some examples and different types of rational numbers that are closed under addition:
Type of Numbers | Addition | Resulting Type of Number |
Rational | \begin{aligned}\dfrac{1}{2} + \dfrac{3}{4} = \dfrac{5}{4}\end{aligned} | Rational |
Integer | \begin{aligned} -4 + 12 = 8\end{aligned} | Integer |
Whole Number | \begin{aligned} 0+ 1200 = 1200\end{aligned} | Whole Number |
Natural Number | \begin{aligned} 100 + 500 = 600\end{aligned} | Natural Number |
These are just some examples showing how rational numbers are closed under addition. The formal proof for the closure property of addition requires more advanced knowledge, so it’s more important to focus on a question that can be easily answered: are irrational numbers also closed under addition?
Why Are Irrational Numbers Not Closed Under Addition?
Irrational numbers are not considered as closed under addition because when an irrational number and its additive inverse are added, the result is equal to zero. As established, zero is a rational number and in fact, a whole number. This counters the definition of the closure property — all members of the set must satisfy the condition.
\begin{aligned}\sqrt{3} + \sqrt{4} &= \sqrt{3} + \sqrt{4}\\ \sqrt{5} + 3\sqrt{5} &= 4\sqrt{5}\\2\pi + 3\pi &= 5\pi\\\dfrac{e}{3} + \dfrac{\sqrt{2}}{3} &= \dfrac{e + \sqrt{2}}{3}\end{aligned}
At first glance, irrational numbers appear to be closed under addition. Take a look at the four examples shown — each of these pairs of irrational numbers returns an irrational number for a sum as well. However, closure property must apply to all irrational numbers for them to be considered as closed under addition.
\begin{aligned} \sqrt{7} + (-\sqrt{7}) &= 0\\ \pi + -\pi&= 0\\2e + (-2e) &= 0\\4\sqrt{5} + (-4\sqrt{5})&= 0\end{aligned}
Since each pair returns a sum of zero and zero is not an irrational number, irrational numbers are not closed under addition. When asked to prove this statement again, just think of counterexamples!
In the next section, explore more particular subsets of numbers that are closed under addition. In addition, learn how to identify a set of numbers that do not satisfy the closure property of addition. When you’re ready, head on over to the sample problems and practice questions!
Example 1
Are even whole numbers closed under addition?
Solution
Even whole numbers are numbers that are divisible by two, such as $\{2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …\}$. When two even numbers are added, their sum will always be even as well. Now, try out different pairs of even numbers first to understand this statement then try to prove it using general forms.
First Even Number | Second Even Number | Sum of Even Numbers |
\begin{aligned}12\end{aligned} | \begin{aligned}14\end{aligned} | \begin{aligned}12 + 14 &= 26 \\ &\Rightarrow\textbf{Even}\end{aligned} |
\begin{aligned}200\end{aligned} | \begin{aligned}48\end{aligned} | \begin{aligned}200 + 48&= 248 \\ &\Rightarrow\textbf{Even}\end{aligned} |
\begin{aligned}580\end{aligned} | \begin{aligned}124\end{aligned} | \begin{aligned}580 + 124&= 704 \\ &\Rightarrow\textbf{Even}\end{aligned} |
Of course, it’s not enough to simply show examples (as we have learned from irrational numbers) to confirm that a group of numbers is closed under addition. Now, how can we prove that even numbers are closed under addition?
Take note that all even numbers are multiples of $2$, so even numbers can be written as a product of a factor and $2$.
- Let the first even number be equal to $2 \cdot k = 2k$.
- Let the second even number equal to $2 \cdot l = 2l$.
Add the two even numbers, $2k$ and $2l$, to observe the resulting sum’s nature.
\begin{aligned}2k + 2l &= 2k + 2l\\&= 2(k + l)\end{aligned}
This means that the sum of the two numbers can be expressed as $2(k + l)$, which is a multiple of $2$ as well and consequently, an even number.
What if there are three or more even numbers?
\begin{aligned}2k_1 + 2k_2 + 2k_3 + …+ 2k_{n- 1} + 2k_n &= 2(k_1 + k_2+k_3+ …+ k_{n -1}+k_n)\end{aligned}
This confirms that the sum of three or more even numbers is also an even number. Hence, it is safe to conclude that even whole numbers are closed under addition.
Example 2
Are odd whole numbers closed under addition?
Solution
Odd whole numbers are whole numbers that end in $1$, $3$, $5$, $7$, or $9$ and it has been established that the sum of two odd numbers will always be even.
First Odd Number | Second Odd Number | Sum of Odd Numbers |
\begin{aligned}21\end{aligned} | \begin{aligned}45\end{aligned} | \begin{aligned}21 + 45 &= 66 \\ &\Rightarrow\textbf{Even}\end{aligned} |
\begin{aligned}157\end{aligned} | \begin{aligned}123\end{aligned} | \begin{aligned}157 + 123&= 280 \\ &\Rightarrow\textbf{Even}\end{aligned} |
\begin{aligned}571\end{aligned} | \begin{aligned}109\end{aligned} | \begin{aligned}579 + 109&= 680 \\ &\Rightarrow\textbf{Even}\end{aligned} |
These three examples are great examples showing that odd whole numbers are not closed under addition. To generalize this as well, recall that odd numbers can be written as $2k + 1$, so observe what happens when two odd whole numbers are added.
\begin{aligned}(2k_1 + 1) + (2k_2 + 1) &= 2k_1 + 2k_2 + 2\\&= 2(k_ 1+ k_2 + 1)\\&\Rightarrow \textbf{Even}\end{aligned}
There is no need to generalize this further — when disproving the closure property of a given set of numbers, all we need are counterexamples! This concludes that odd whole numbers are not closed under addition.
Apply a similar process when trying to determine whether a group of numbers is closed under addition or not. Use their properties to generalize the closure property for all numbers and look out for counterexamples to quickly disprove statements. When ready to test your understanding of closure property under addition, head on over to the section below!
Practice Questions
1. Which of the following numbers are closed under addition?
A. Odd Integers
B. Irrational Numbers
C. Perfect Squares
D. Even Integers
2. Which of the following numbers are not closed under addition?
A. Natural Numbers
B. Fractions
C. Odd Numbers
D. Even Numbers
3. True or False: The sum of two irrational numbers will always be rational numbers.
4. True or False: The sum of two numbers divisible by $5$ will always be whole numbers.
5. True or False: Positive decimals are closed under addition.
6. Which of the following irrational numbers will return a rational number when added to $2\sqrt{3}$?
A. $-4\sqrt{3}$
B. $-2\sqrt{3}$
C. $2\sqrt{3}$
D. $4\sqrt{3}$
7. Are multiples of $4$ closed under addition?
A. Yes
B. No
8. Are prime numbers closed under addition?
A. Yes
B. No
9. Fill in the blank to make the statement true:
The addition sentence $4 + 109 = 113$ shows that __________.
A. odd numbers are closed under addition.
B. whole numbers are not closed under addition.
C. whole numbers are closed under addition.
D. odd numbers are not closed under addition.
10. Fill in the blank to make the statement true:
The addition sentence $\dfrac{1}{2} + \dfrac{1}{2} = 1$ shows that __________.
A. rational numbers are closed under addition.
B. irrational numbers are not closed under addition.
C. irrational numbers are closed under addition.
D. rational numbers are not closed under addition.
Answer Key
1. D
2. C
3. False
4. True
5. True
6. B
7. Yes
8. No
9. C
10. A
