• Home
  • >
  • Derivative of Absolute Value – Definition Properties, and Examples

Derivative of Absolute Value – Definition Properties, and Examples

Derivative of Absolute Value Definition Properties and

In this post, we will go deeply into the fascinating realm of the derivative of absolute value, solve its puzzles, and investigate its uses. This voyage promises intriguing insights, whether you’re a student seeking clarification or a maths enthusiast pursuing curiosity.

Defining Derivative of Absolute Value

The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point.

The absolute value function is defined as:

\begin{cases} x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}
 
Given its piecewise definition, the derivative of the absolute value function can also be found piecewise. However, there’s a catch.
 
The function |x|  is not differentiable at x = 0 because it has a sharp turn (cusp) at this point. Away from this point, the function is linear and thus differentiable. The derivative of |x| is given by: \[ \frac{d}{dx} |x| = \begin{cases} 1 & \text{if } x > 0 \\ -1 & \text{if } x < 0 \\ \text{undefined} & \text{if } x = 0 \end{cases} \] This definition highlights the rate of change of the absolute value function at any point \( x \), except at the origin, where it’s undefined due to the sharp change in direction.

Example

Function,  t(x) = |$x^2$ + 2x – 3|

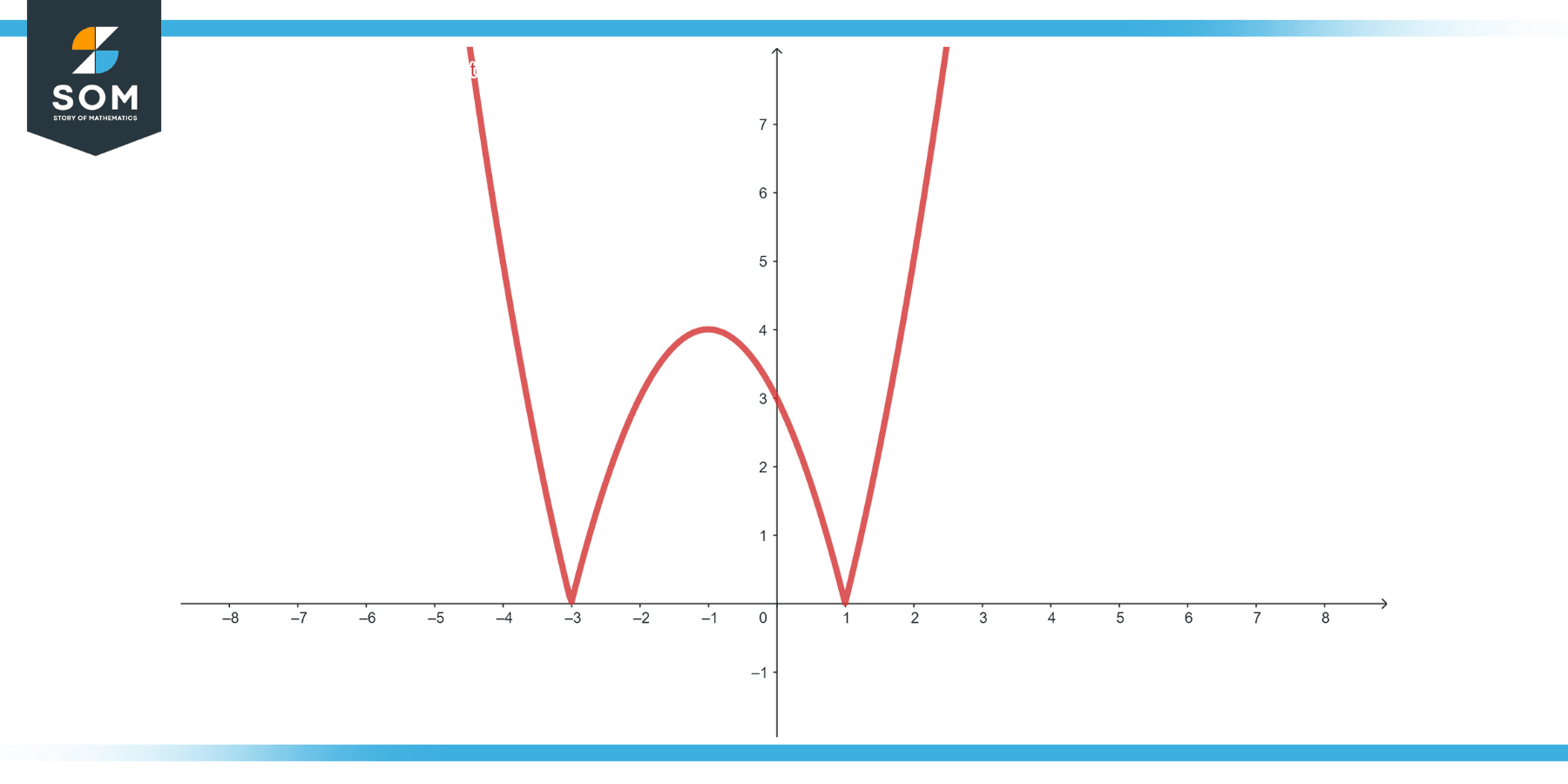
Graphical representation of the function y equals absolute value of x square plus 2x minus 3
Figure-1.

Solution

Use the chain rule. t'(x) = \[ \begin{cases} 2x + 2 & \text{if } x^2 + 2x – 3 > 0 \\ -(2x + 2) & \text{if } x^2 + 2x – 3 < 0 \\ \text{undefined} & \text{wherever } x^2 + 2x – 3 = 0 \end{cases} \]

Properties of Derivative of Absolute Value

Derivatives capture the rate of change or the slope of a function at a specific point. When dealing with the absolute value function, there are unique properties and behaviors we need to consider, mainly because of its piecewise nature. Let’s delve into the properties of the derivative of the absolute value function:

Non-Differentiability at the Origin

The absolute value function has a sharp turn (or cusp) at the point . This means that the function does not have a well-defined tangent at this point, making its derivative undefined at .

Linear Away from the Origin

For all values x , the absolute value function is linear. This means that its rate of change or slope is constant in these regions.

Positive Slope for Positive x-values

For all , the derivative of is 1. This indicates that the function is increasing at a constant rate in this interval.

Negative Slope for Negative x-values

For all , the derivative of is -1. This means the function is decreasing at a constant rate in this interval.

Piecewise Derivative

Given the above points, the derivative of the absolute value function can be represented as a piecewise function:
\begin{cases} 1 & \text{if } x > 0 \\ -1 & \text{if } x < 0 \\ \text{undefined} & \text{if } x = 0 \end{cases}

Symmetry

The absolute value function is symmetric about the y-axis. However, this symmetry translates into an asymmetry for its derivative. The rate of change is positive on the right of the y-axis and negative on the left.

Continuity

While the absolute value function is continuous everywhere, its derivative is discontinuous at x = 0. This is a reflection of the fact that a function can be continuous at a point but not differentiable there.

Higher-Order Derivatives

The second derivative of  |x| does not exist for any real number because its first derivative is discontinuous at x = 0  and non-constant elsewhere.

When using the absolute value function in calculus, it’s essential to comprehend these characteristics, especially when dealing with issues that call for differentiation, slope analysis, or thinking about how the function behaves in respect to its derivative.

Exercise

Example 1

Function,

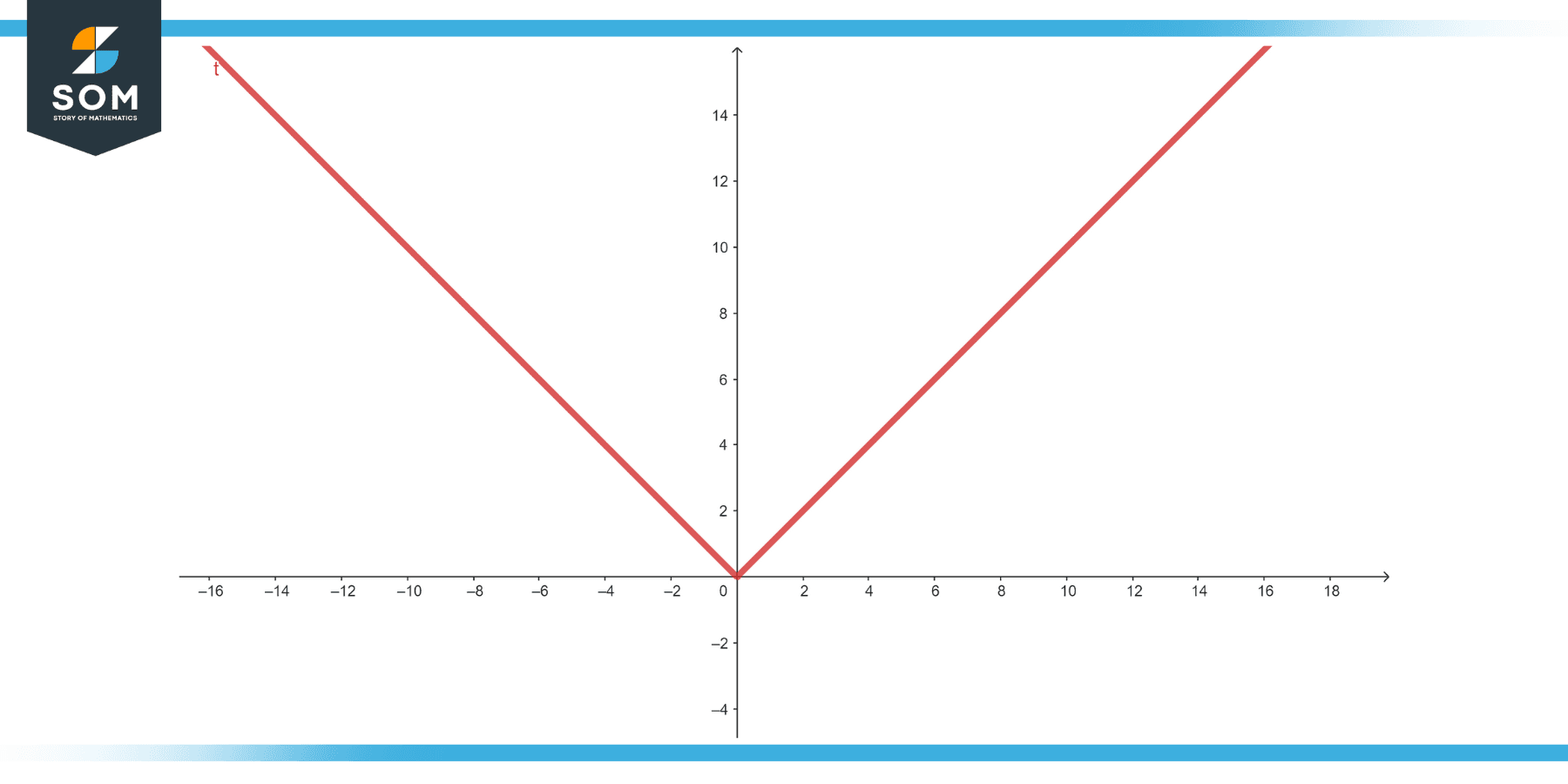
Graphical representation of the function y equals absolute value of

Figure-2.

Solution

As discussed earlier,

\begin{cases} 1 & \text{if } x > 0 \\ -1 & \text{if } x < 0 \\ \text{undefined} & \text{if } x = 0 \end{cases} \]

Example 2

Function, g(x) = x + |x|

Solution

Differentiate term by term. g'(x) = 1 + f'(x) = \[\begin{cases} 2 & \text{if } x > 0 \\ 0 & \text{if } x < 0 \\ \text{undefined} & \text{if } x = 0 \end{cases} \]

Example 3

Function, \( h(x) = x^2 |x| \)

Solution

Use the product rule. \[ h'(x) = x^2 \cdot f'(x) + 2x \cdot |x| = \begin{cases} 3x^2 & \text{if } x > 0 \\ -x^2 & \text{if } x < 0 \\ 0 & \text{if } x = 0 \end{cases} \]

Example 4

Function,  p(x) = |$x^2$ – 4|

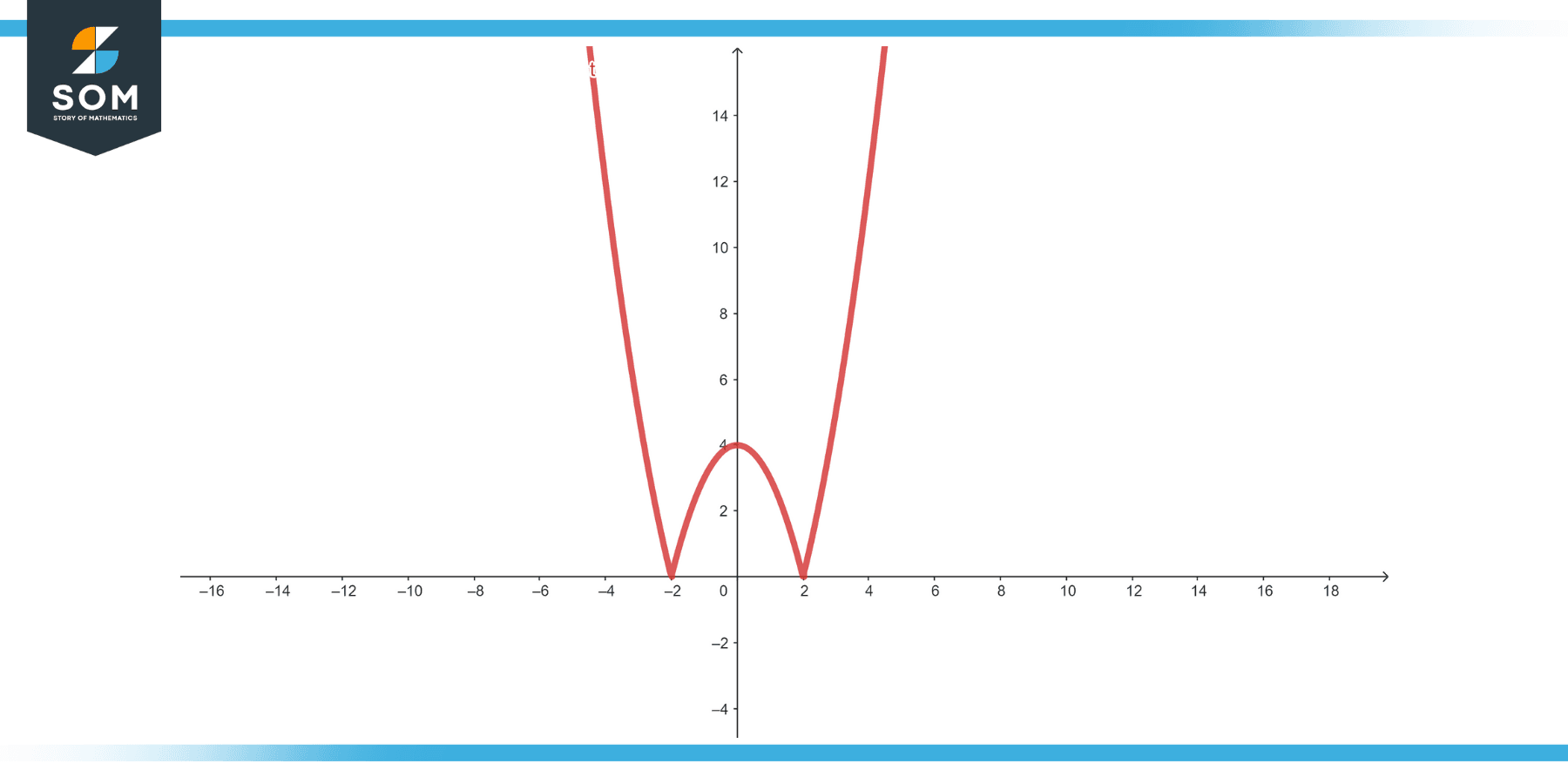
Graphical representation of the function y equals absolute value of x square minus 4
Figure-3.

Solution

p'(x) = \[ \begin{cases} 2x & \text{if } x^2 > 4 \text{ (i.e., } x > 2 \text{ or } x < -2) \\ -2x & \text{if } x^2 < 4 \text{ (i.e., } -2 < x < 2) \\ \text{undefined} & \text{if } x = 2 \text{ or } x = -2 \end{cases} \]

Example 5

Function,  q(x) = |x| + |x-1| 

Solution

Differentiate each term individually.  q'(x) = \[\begin{cases} 2 & \text{if } x > 1 \\ 0 & \text{if } x < 0 \\ 1 & \text{if } 0 \leq x \leq 1 \\ \text{undefined} & \text{if } x = 0 \text{ or } x = 1 \end{cases} \]

Example 6

Function,  r(x) = |2x + 1| – |x – 3|

Solution

Differentiate each term individually. r'(x) = \[ \begin{cases} 1 & \text{if } x > 3 \\ 3 & \text{if } x < -1/2 \\ 2 & \text{if } -1/2 \leq x \leq 3 \\ \text{undefined} & \text{if } x = 3 \text{ or } x = -1/2 \end{cases} \]

Example 7

Function, s(x) = $x^3$ |x|

Solution

Use the product rule. s'(x) = \[ 3x^2 |x| + x^3 f'(x) = \begin{cases} 4x^3 & \text{if } x > 0 \\ 0 & \text{if } x = 0 \\ -2x^3 & \text{if } x < 0 \end{cases} \]

Applications 

The derivative of absolute value function, while a fundamental topic in calculus, finds its applications in several areas of study and real-world situations. Understanding the behavior of and its rate of change is essential in these contexts:

  • Optimization Problems

    • In economics, the absolute value can represent the deviation of a certain quantity from an ideal or target value. For purposes of optimization, the derivative can be quite useful in determining how this deviation changes.

  • Signal Processing

    • Understanding signal deviations and anomalies are aided by the absolute value function and its derivatives, particularly when working with amplitude-based data.

  • Physics

    • The absolute value in physics can represent magnitudes or distances from reference points, particularly in the study of mechanics.

  • Mathematical Modelling

    • Situations, where quantities deviate from a norm or target, can be modeled using the absolute value function. The derivative assists in understanding the sensitivity or rate of change of such deviations.

  • Machine Learning and Data Analysis

    • In certain algorithms, the absolute difference between predicted and actual values (known as the L1 norm) is minimized. The derivative is crucial when applying gradient-based methods to minimize this difference.

  • Finance

    • In financial modeling, the absolute value can represent deviations or differences between actual and projected values. The derivative can provide insights into the volatility or rate of change of such differences.

  • Operations Research

    • Absolute values are often used in formulating linear programming problems, especially in cases involving deviations from specific values. The derivative aids in the sensitivity analysis of these models.

  • Geometry

    • When studying geometric objects, the absolute value can represent distances or magnitudes. The derivative gives information about the variation of these distances, especially in dynamic geometrical situations.

  • Environmental Science

    • In environmental studies, the absolute value might denote deviations of certain parameters (like pollution levels) from acceptable or standard levels. The derivative aids in understanding the rate at which these deviations are occurring.

  • Robust Statistics

    • In statistics, absolute deviations as opposed to squared deviations are sometimes used to measure dispersion because of their resistance to outliers. Derivatives of these metrics become relevant when looking for optimal solutions or understanding variations.

All images were created with GeoGebra.