JUMP TO TOPIC

Our journey through this article will illuminate the nuances of e^infinity ($e^∞$), shedding light on its mathematical implications, its role in defining the boundaries of mathematical growth, and its wide-ranging applications in science and engineering.
Whether you are a veteran mathematician, an enthusiastic STEM student, or simply a curious intellect seeking to unravel mathematical marvels, prepare for a riveting exploration of e^Infinity ($e^∞$) — an infinity that’s not just larger than large but also fascinatingly exponential.
Definition
The expression e^Infinity ($e^∞$) pertains to an exponential function using the mathematical constant ‘e.’ Euler’s number ‘e‘ is an important mathematical constant approximately equal to 2.71828 and is the base of the natural logarithm.
When we raise ‘e‘ to the power of infinity (e^Infinity) ($e^∞$), it denotes a mathematical limit scenario. Given that ‘e‘ is greater than 1, as you make the exponent larger and larger, the overall value of e^Infinity ($e^∞$) will grow without bounds. Thus, in mathematical terms, e^Infinity is considered to be infinite or undefined.
However, it’s important to remember that “infinity” is not a traditional “number” in the same sense as integers or real numbers. Instead, it’s a concept that represents an unbounded quantity. Therefore, when we say e^Infinity ($e^∞$) equals infinity, we mean that the value of the expression grows without limit as the exponent becomes arbitrarily large.
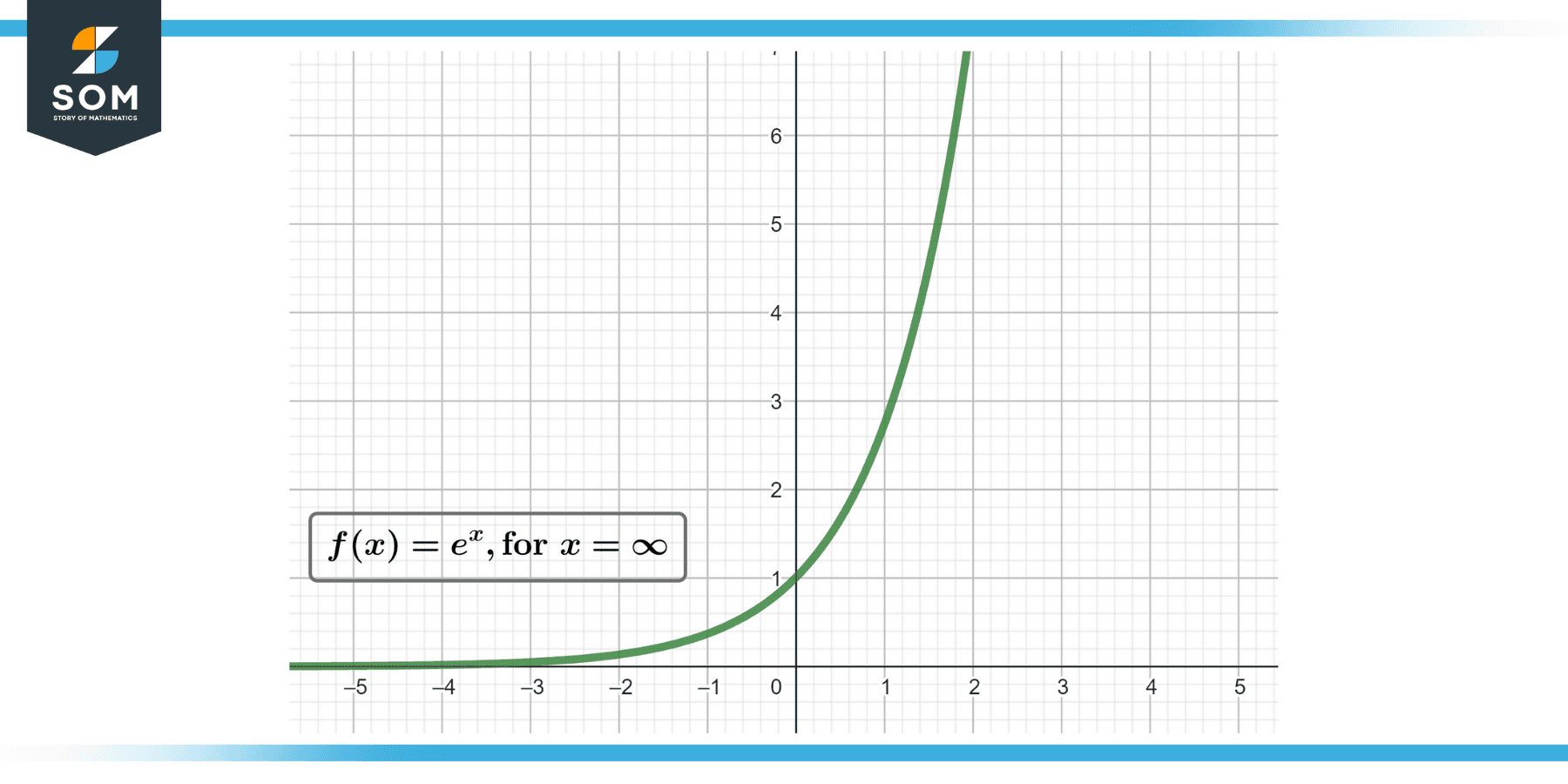
Figure-1.
Properties
The expression e^infinity ($e^∞$) doesn’t have “properties” in the traditional sense like a geometric shape, or a set of numbers might have because infinity is not a typical number but rather a concept signifying an unbounded quantity.
However, the expression e^infinity ($e^∞$) does have certain behaviors and characteristics in a mathematical context, particularly in calculus and analysis:
Limit Behavior
The expression e^infinity ($e^∞$) is used to describe a limit, specifically, the limit as the exponent of e tends to infinity. Since e (approximately equal to 2.71828) is greater than 1, as the exponent gets larger and larger, the value of e to that power also gets larger.
So, the limit of eᵡ as x approaches infinity is infinity. In mathematical notation, this is written as lim (x->∞) eᵡ = ∞.
Growth Rate
The expression e^infinity ($e^∞$) symbolizes a rapid, unbounded growth rate. When you have a quantity that grows at a rate proportional to its current size—like compound interest, or population growth in an idealized scenario—that growth can be modeled using e raised to a power. When that power tends towards infinity, the growth is essentially explosive, getting indefinitely large.
Comparison to Other Functions
When compared to polynomial functions, e^infinity ($e^∞$) grows much faster. This is a manifestation of the fact that any exponential function eventually outpaces any polynomial, no matter how large the degree of the polynomial. For example, the limit as x approaches infinity of (xⁿ / eᵡ) is 0 for any positive integer n, meaning that eᵡ gets infinitely large much faster than xⁿ does.
Inverse and Derivative
The inverse function of eᵡ is the natural logarithm, ln(x), and interestingly, the derivative of eᵡ with respect to x is also eᵡ. This makes eᵡ (and therefore e^infinity ($e^∞$)) particularly important in calculus and differential equations.
Again, it’s crucial to understand that the concept of “infinity” is more of a mathematical idea used to describe a quantity without bounds rather than a conventional number. Therefore, e^infinity ($e^∞$) is a way of describing behavior as one moves towards this unbounded quantity in the context of exponential functions.
Ralevent Formulas
In mathematical terms, e^infinity ($e^∞$) is essentially a statement about limit behavior — the behavior of the function eᵡ as x approaches infinity.
Although we don’t have specific formulas for e^infinity ($e^∞$), we have several mathematical formulas and rules that often apply when dealing with the function eᵡ, particularly in limit scenarios.
Exponential Limit Formula
The basic rule of limits that applies here is that the limit as x approaches infinity of eᵡ is infinity. Mathematically, this is expressed as:
lim (x→∞) eᵡ = ∞
L’Hopital’s Rule
This rule is used when evaluating the limit of the quotient of two functions, both of which approach zero or both of which approach infinity (referred to as indeterminate forms 0/0 or ∞/∞). In these scenarios, the limit of the quotient equals the limit of the quotients of their derivatives. This can often apply to expressions involving eᵡ.
For instance, for an indeterminate form 0/0:
lim (x→0) (eᵡ - 1) / x
Using L’Hopital’s Rule (which states that this limit is the same as the limit of the ratio of their derivatives), we get:
lim (x→0) (eᵡ) / 1 = e⁰ = 1
Natural Logarithm and Exponential Functions
The natural logarithm function, ln(x), is the inverse of the exponential function with base e. This means that:
$e^{ln(x)}$ = x for all x > 0, and ln(eᵡ) = x for all real numbers x.
Derivative and Integral of eᵡ
One of the most crucial properties of the function eᵡ is that it is its own derivative and integral. So we have:
d/dx [eᵡ] = eᵡ
and
∫ eᵡ dx = eᵡ + C
where C is the constant of integration.
Comparative Growth Rates
As x approaches infinity, any polynomial function will grow at a slower rate than an exponential function like eᵡ. Mathematically, for any positive integer n:
lim (x→∞) xⁿ / eᵡ = 0
Euler’s Identity
Although it doesn’t directly involve e^infinity ($e^∞$), Euler’s identity is one of the most celebrated formulas involving e. It states that:
$e^{(iπ)}$ + 1 = 0
Exercise
Example 1
Limit Behavior of eᵡ
Find lim (x->∞) eᵡ.
Solution
Since eᵡ grows indefinitely as x grows, lim (x->∞) eᵡ = ∞.
Example 2
Inverse Function
Find lim (x->∞) ln(eᵡ).
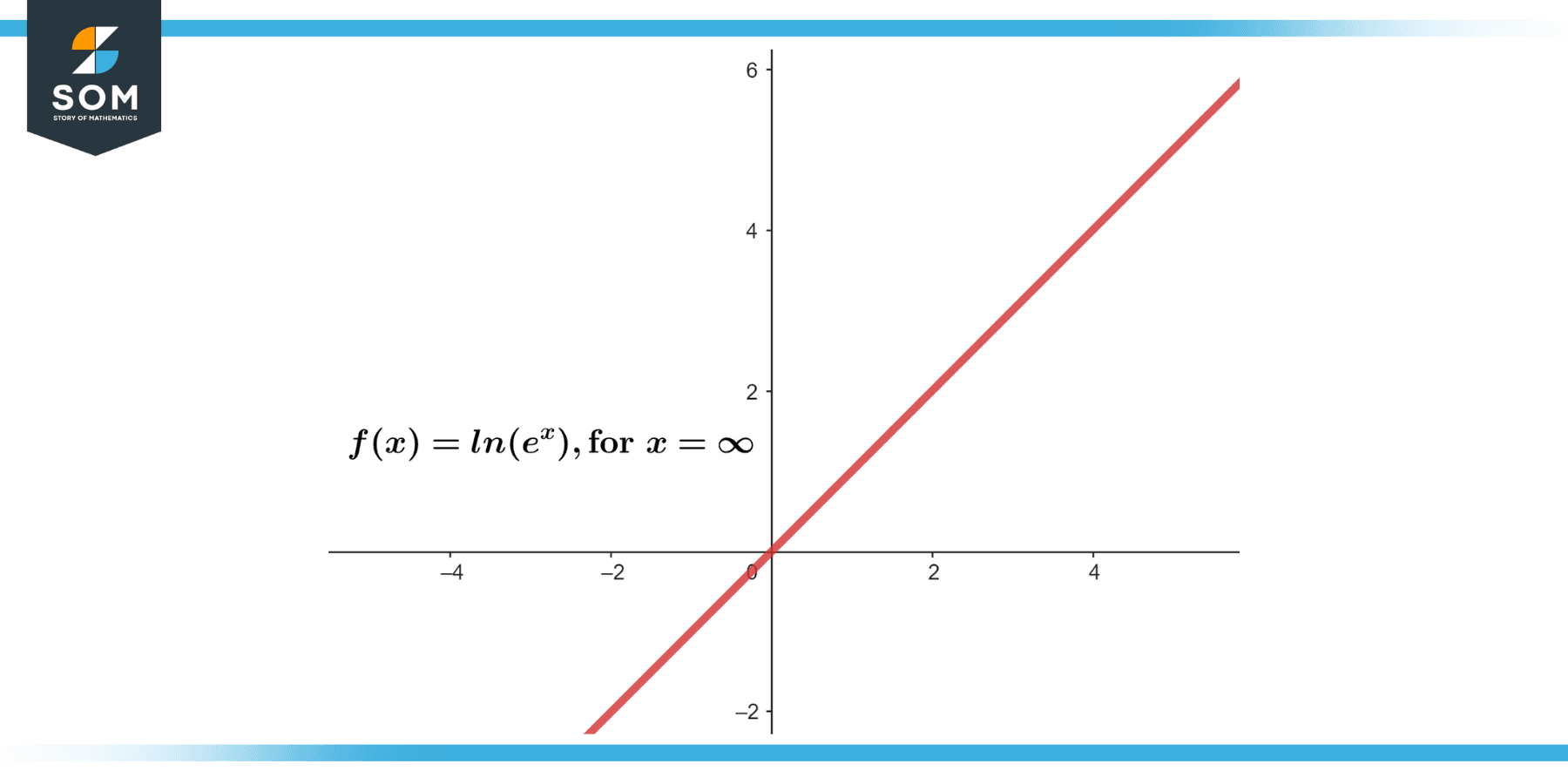
Figure-2.
Solution
Since the natural logarithm ln(x) is the inverse function of eᵡ, ln(eᵡ) simplifies to x. Therefore:
lim (x->∞) ln(eᵡ) = ∞
Example 3
Growth Rate Comparison 1
Find lim (x->∞) (x³ / eᵡ).
Solution
Since eᵡ grows faster than any polynomial function of x as x approaches infinity:
lim (x->∞) (x³ / eᵡ) = 0
Example 4
Growth Rate Comparison 2
Find lim (x->∞) (eᵡ / x!).
Solution
For large x, x factorial (x!) grows faster than eᵡ. Therefore:
lim (x->∞) (eᵡ / x!) = 0
Example 5
L’Hopital’s Rule Application 1
Find lim (x->0) (eᵡ – 1) / x.
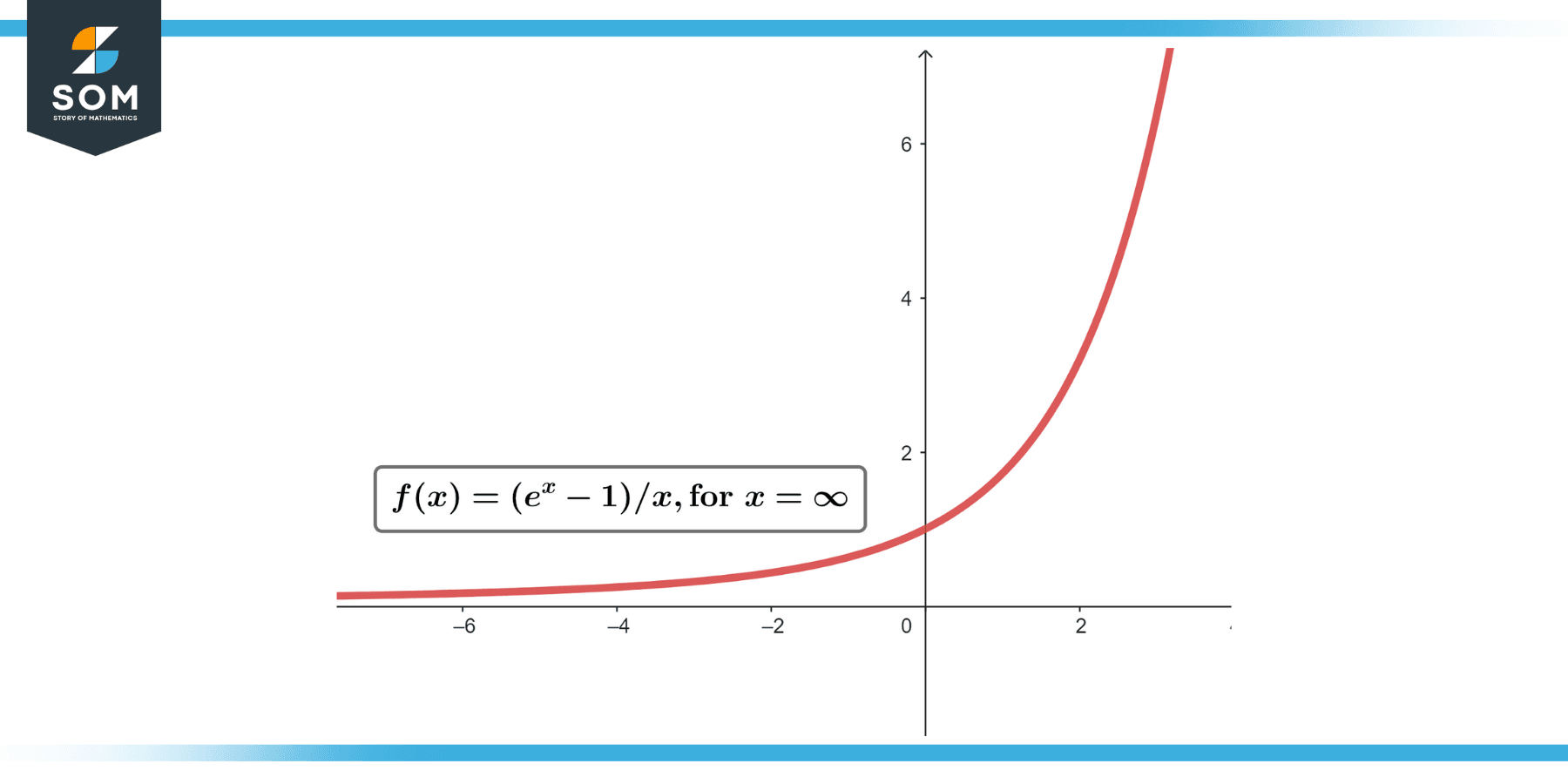
Figure-3.
Solution
This is an indeterminate form (0/0) as x approaches 0. Using L’Hopital’s rule, we differentiate the numerator and the denominator to get:
eᵡ / 1
Thus:
lim (x->0) (eᵡ – 1) / x = e⁰ = 1
Example 6
L’Hopital’s Rule Application 2
Find lim (x->∞) (eᵡ / x²).
Solution
As x approaches infinity, the numerator and the denominator approach infinity, so this is an indeterminate form (∞/∞).
Using L’Hopital’s rule, we differentiate the numerator and the denominator to get eᵡ / 2x. Thus, we need to continue differentiating until we obtain a determinate form. After another round of L’Hopital’s rule, we have:
eᵡ / 2
which equals ∞ as x approaches ∞.
Example 7
Exponential Decay
Find lim (x->∞) e-ᵡ.
Solution
Since e-ᵡ represents an exponential decay, as x gets larger, e-ᵡ tends towards 0. So:
lim (x->∞) e-ᵡ = 0
Example 8
Inverse Exponential Growth
Find lim (x->∞) 1 / eᵡ.
Solution
This is the same as the previous example, as 1 / eᵡ simplifies to e-ᵡ. So:
lim (x->∞) 1 / eᵡ = 0
Applications
The term e^infinity ($e^∞$) itself is largely theoretical, as it represents a value that grows without bounds. However, the underlying function, eᵡ, is highly applicable in a variety of fields, particularly when dealing with growth rates, change, or unbounded behavior. Here’s how it applies in some fields:
Mathematics and Physics
The base ‘e‘ is fundamental to calculus and is often used in equations representing growth or decay, differential equations, probability theory, and complex numbers. In physics, ‘e‘ often appears in equations related to exponential growth or decay, such as populations, radioactive decay, or charging and discharging capacitors.
Economics and Finance
Exponential functions with base ‘e‘ are used to calculate compound interest, which can grow at an incredibly rapid pace – towards infinity, in theory, if no real-world limitations are applied.
Computer Science
In the field of algorithms and complexity theory, the time complexity of certain algorithms can grow exponentially, and this could be represented as an exponential function, such as eᵡ. While e^infinity ($e^∞$) wouldn’t be directly used, understanding this limit behavior is important in evaluating the efficiency of algorithms.
Biology
Exponential growth with base ‘e‘ is often used to model population growth under ideal conditions. In the real world, limiting factors prevent populations from reaching ‘infinity‘, but the model is still very useful for understanding rates of growth.
Statistics and Data Science
The concept of ‘e‘ is central to the probability density function of the normal distribution, which is fundamental in statistics. Also, logarithms base ‘e‘ are widely used in multiple statistical methods and in machine learning algorithms.
Remember, the concept of e^infinity ($e^∞$) is more of a mathematical abstraction signifying behavior as a variable tends towards infinity. This is not usually directly applicable in real-world scenarios as we don’t deal with actual infinities in practice.
But the concept does help us understand how certain quantities might behave under specific conditions or in theoretical scenarios.
All images were created with GeoGebra.
