JUMP TO TOPIC
 The domain and range of radical functions are the possible input and output values of the function.
The domain and range of radical functions are the possible input and output values of the function.
If $f(x)$ is a radical function, then all the possible input values are the domain of the function while all the possible outputs are the range of the function. In this complete guide, we discuss in detail how to determine the domain and range of different radical functions.
Domain of a Radical Function
The domain of a radical function is the set of all the possible input values of the function. This means that any input values which do not make the function undefined or complex will be termed as the domain of a radical function.
A radical function or a square root function is a function which consists of a variable or variables that are present under a square root; hence it is also called a square root function. For example, the function $\sqrt {x^{2} – 6}$ will be considered as a radical function.
How To Determine the Domain of a Radical Function?
To determine the domain of the radical function, we will exclude all the values which either make the function undefined or complex or, in other words, all sets of values which results in a defined or actual number output will be termed as the domain of the radical function.
In order to find out the domain of the radical function, we must first identify the radicant of the radical function i.e. we must identify the independent variable under the square root. For example, if we are given the function $\sqrt {x + 2}$, then “$x$” can have all the values equal to or greater than $-2$; any value less than $-2$ will make the function a complex function. Hence, the domain of the function will be all the real numbers greater or equal to “$-2$” or $x \geq -2$.
So the domain will contain all the numbers except those which make the square root function / radicant negative or give us a complex function.
Range of a Radical Function
The range of a radical function is defined as the set of all the output values of the function. These output values are calculated through a set of all the possible input values. The range of the radical function will always be a real number. It cannot be an undefined or complex number.
The range of the radical function can only be determined if the inverse of the function can be calculated. The range of the radical function also is considered as the input values for the inverse of the original function. For example, if we have a function $y = f(x)$, then “x” will be an input of the function and “f(x)” will be the output, but for an inverse function, f(x) will be the input and it will produce output “x”.
How To Determine the Range of a Radical Function?
The range of a radical function can easily be calculated by simply putting the minimum and maximum possible input value in the function, and it will give us the range of the square root function / radical function.
For example, for the radical function $\sqrt {x + 2}$, the minimum value of “$x$” as an input will be “$-2$” and the output at this value is “$0$.” Hence, the range of the given function will be greater than or equal to zero as the maximum possible value for “$x$” can be any real number. The range of the given function can be written as $y \geq 0$.
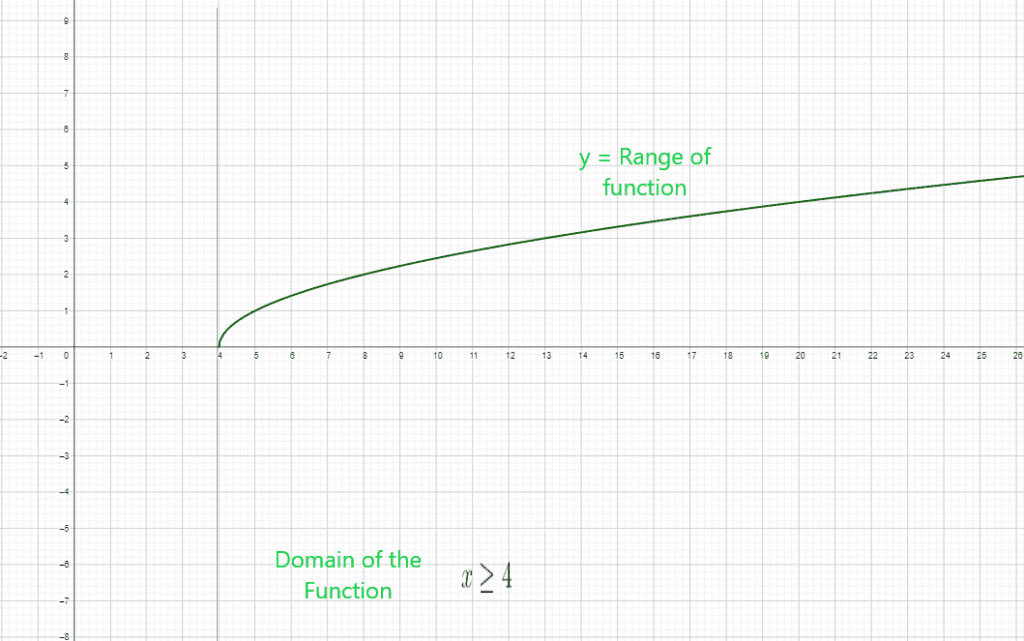
Example 1: Find out the domain and range of the following radical functions.
- $y = \sqrt{x – 4}$
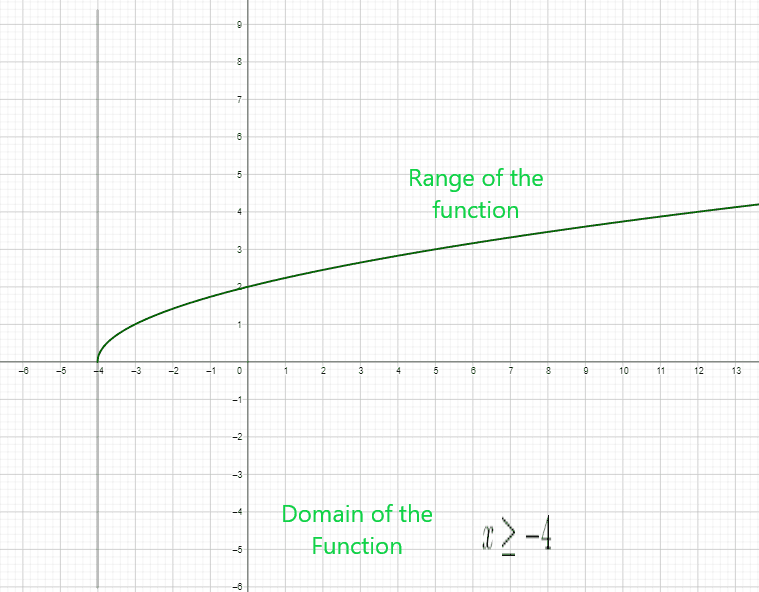
- $y = \sqrt{x + 4}$
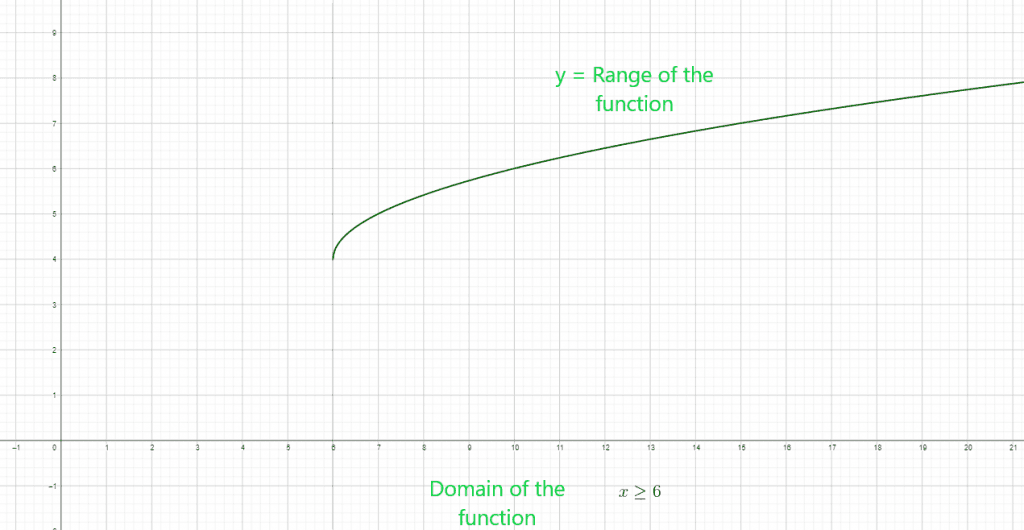
- $y = \sqrt{x – 6} + 4$
Solution:
1).
We know that to determine the domain of the given function, the independent variable “$x$” can have all the values at which the radicant is not negative. The domain of a radical function should be $\sqrt{f(x)} \geq 0$.
In this case, the term $x – 4$ should be greater or equal to zero, hence we can write it as:
$x – 4 \geq 0$
adding “$4$” on both sides:
$x – 4 + 4 \geq 4$
$x \geq 4$ is the domain of the function.
The range of the function will start from the minimum output, which in this case will be “$0$”. A question is raised on how to determine the range of a radical function algebraically.
The range of a radical function can be determined by using the general form the range of the equation can be written as $\sqrt [m] {ax + b} + c$. If we compare this to the original equation, the value of “$c$” is $0$. So, the minimum value of the range should be 0; hence the range of the function should be greater or equal to zero.
The domain and range of square root function interval notation can be represented as:
Domain of the radical function $= [ 4 , \infty )$
Range of the radical function = $[ 0 , \infty )$
The brackets are showing interval notations. The bracket “[“shows a closed interval while”)” shows an open interval.
2).
The radicant cannot be negative while finding out the domain of the radical function; the independent variable “x” can have all the values at which the radicant is not negative.
The term $x + 4$ will not be negative if the value of “$x$” is greater or equal to “$-4$”. So we can write it as:
$x + 4 \geq 0$
subtracting “$4$” on both sides:
$x + 4 – 4 \geq – 4$
$x \geq -4$ is the domain of the function.
The range of the function will start from the minimum output, which in this case will be “0”. If we compare this to the original equation, the value of “c” is 0. So the minimum value of the range should be 0; hence, the range of the function should be greater or equal to zero.
Domain of the radical function $= [ – 4 , \infty)$
Range of the radical function $= [ 0 , \infty )$
3).
We know that to determine the domain of the given function, the independent variable “x” can have all the values at which the radicant is not negative. The domain of a radical function should be such that the radicant part of the equation should be greater than zero.
In this case, the term x – 6 should be greater or equal to zero, so we can write it as:
$x – 6 \geq 0$
adding “$6$” on both sides:
$x – 4 + 6 \geq 6$
$x \geq 6$ is the domain of the function.
The general form of the range of the equation can be written as $\sqrt [m] {ax + b} + c$. The value of “c” in this case will be 4. Hence, the value of the range should be greater than or equal to 4.
Domain of the radical function $= [6 , \infty )$
Range of the radical function = $[4 , \infty)$
Example 2: Find out the domain and range of the following radical functions:
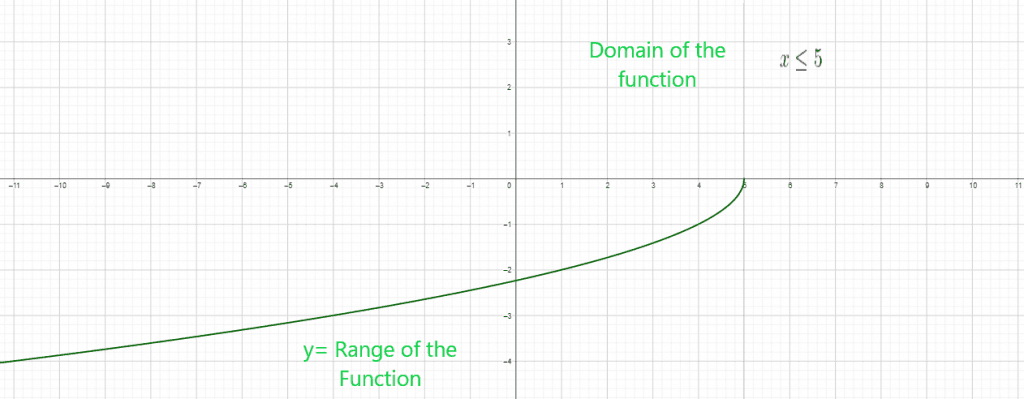
1. $y = -\sqrt{5 – x}$
2. $y = \sqrt [3]{3x – 6} + 7$
1).
We know that to determine the domain of the given function, the radicant cannot be negative. It can be zero or positive, so the value of “$x$” should be less than or equal to “$-5$”.
In this case, the term $5 – x$ should be greater or equal to zero, so we can write it as:
$5 – x \geq 0$
Subtracting “$-5$” on both sides:
$5 – 5 -x \geq -5$
$-x \geq – 5$
Multiplying both sides by “$-1$” and changing the direction sign:
$x \leq 5$
The range of the function, in this case the minimum output, will be “0” and by comparing it to the general equation, we know the value of “c” is equal to zero. Hence, the domain and range of the radical function can be written as:
Domain of the radical function $= [- \infty, 5)$
Range of the radical function $= [ – \infty, 0)$
2).
We are given a cube root. Finding the domain of the function is easy as we know the radicant cannot be negative. While finding out the domain of the radical function, the independent variable “x” can have all the values at which the radicant is not negative.
The term $3x – 6$ will not be negative if the value of “$x$” is greater or equal to “$2$”, so we can write it as:
$3x – 6 \geq 0$
Adding “$6$” on both sides
$3x – 6 + 6 \geq 6$
$3x \geq 6$
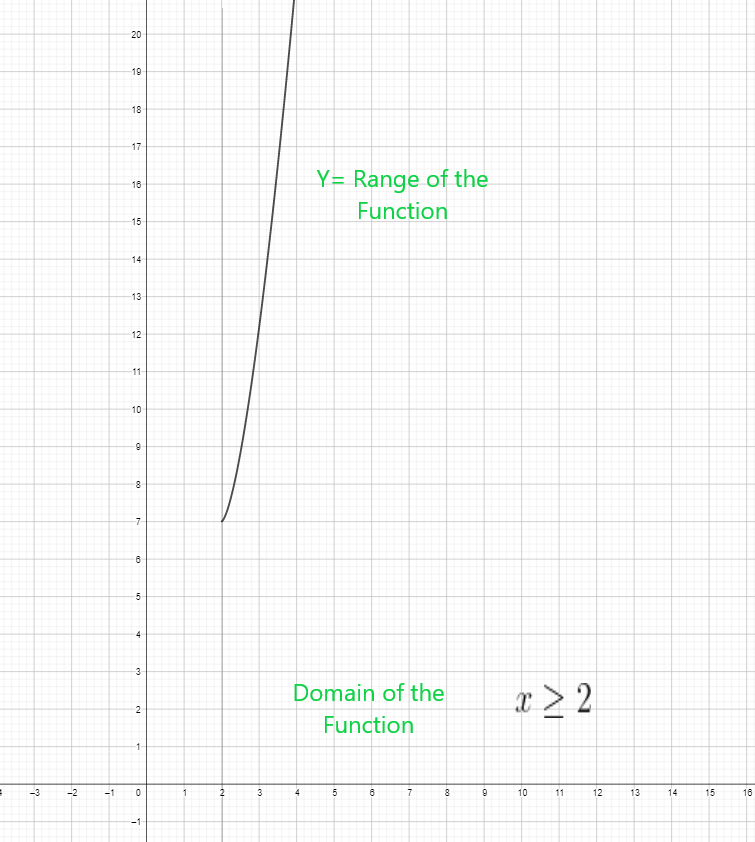
$x \geq 2$
The range of the function will start from the minimum output, which in this case will be zero. We will write the domain and range of the function as:
Domain of radical function $= [ 2 , \infty)$
Range of the radical function $= [ 0 , \infty )$
Practice Questions:
- Determine the domain and range of the function $-\sqrt{8 – x}$.
- Find the domain and range of the given function $-\sqrt{18 – 2x}$.
- Is the domain and range of rational functions determined in the same manner as radical functions?
Answer Key:
1).
Domain of the radical function $= [- \infty, 8)$
Range of the radical function = $[ – \infty, 0)$
2).
Domain of the radical function $= [- \infty, 9)$
Range of the radical function = $[ – \infty, 0)$
3).
Domain and range of the rational function are determined in a slightly different manner. A rational function does not include any square root term, so if you are asked a question about how to find the domain of a rational function, then the answer is simple any input value which does not make a rational function undefined is the domain of the function, and the corresponding outputs are a range of the rational function.
