JUMP TO TOPIC
 Shaded triangles are provided in a variety of ways in mathematics so that their area can be calculated using an appropriate method. A triangle is a three-edged polygon having three vertices. It is a fundamental shape in geometry.
Shaded triangles are provided in a variety of ways in mathematics so that their area can be calculated using an appropriate method. A triangle is a three-edged polygon having three vertices. It is a fundamental shape in geometry.
This complete guide will teach you about different types of triangles as well as the methods for calculating the area of a shaded triangle.
How To Find the Area of a Shaded Triangle
To determine the area of a shaded triangle, you normally need to subtract the area of a smaller interior shape from the area of a larger outer shape. If one of the shapes is a composite shape, you must split it up it into shapes for which you have area formulas.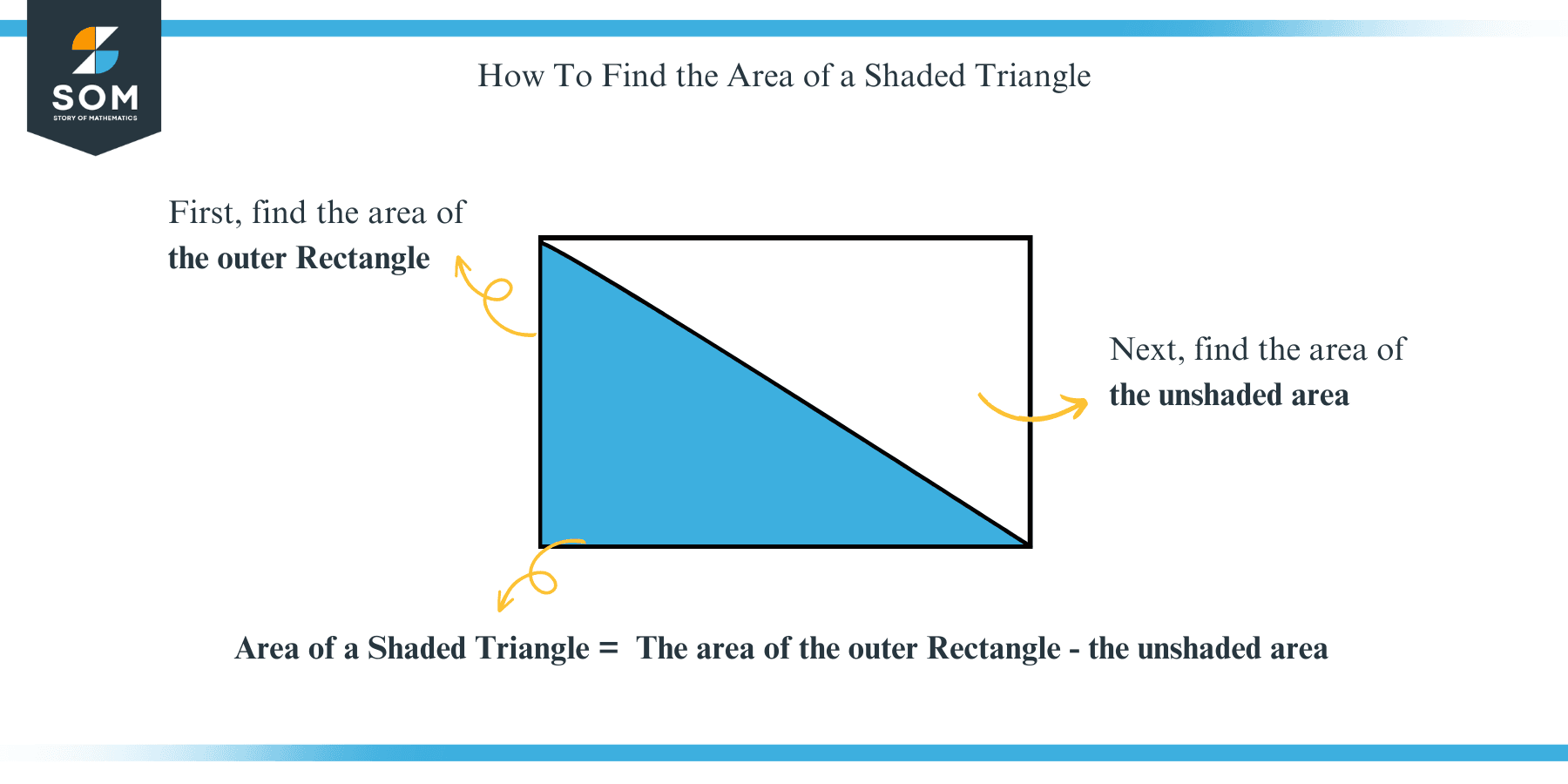
Examples
You may be asked to determine the area of shaded regions in some problems. Let’s look at some examples to gain knowledge on how to determine the area of a shaded triangle.
Example 1
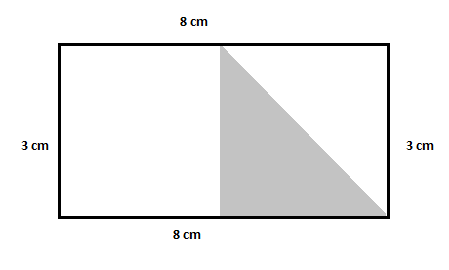
Consider the shaded triangle in the following figure. Work out the area of the shaded triangle.
Solution
Examine the given diagram. To find the area of the shaded triangle, you can see that the figure contains one shaded triangle, an unshaded triangle, and an unshaded rectangle inside a rectangle. To find the area of the shaded triangle, you first need to find the area of the bigger rectangle and then subtract it from the area of the unshaded rectangle plus the area of the unshaded triangle.
Area of the bigger rectangle $=3\times 8=24\,cm^2$
Area of the unshaded rectangle $=4\times 3=12\,cm^2$
Area of the unshaded triangle $=\dfrac{1}{2}\times 4\times 3=6\,cm^2$
Area of the shaded triangle $=$ Area of the rectangle $-$ Area of the unshaded region
Area of the shaded triangle $=24-(12+6)=24-18=6\,cm^2$
Example 2
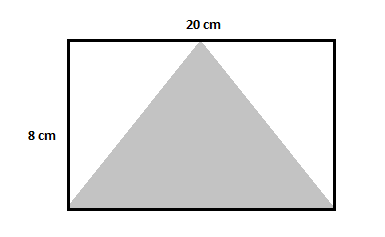
Find the area of the shaded triangle in the figure given below.
Solution
This figure has one bigger rectangle, two unshaded, and one shaded triangle. First, find the area of the rectangle and subtract the area of both the unshaded triangles from it as done in the previous example.
Area of the bigger rectangle $=20\times 8=160\,cm^2$
Area of the first unshaded triangle $=\dfrac{1}{2}\times 8\times 10=40\,cm^2$
You can see that both unshaded triangles have the same bases and heights, and therefore will have the same area. So:
Area of the second unshaded triangle $=\dfrac{1}{2}\times 8\times 10=40\,cm^2$
Area of the shaded triangle $=$ Area of the rectangle $-$ Area of the unshaded triangles
Area of the shaded triangle $=160-(40+40)=160-80=80\,cm^2$
Example 3
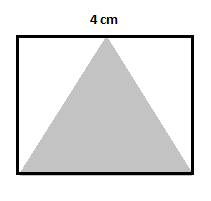
Consider a similar example with a square given in the figure and find the area of the shaded triangle.
Solution
First, find the area of the square. Let $A$ be the area of the square, then:
$A=(4\,cm)^2=16\,cm^2$
Next, find the areas of two unshaded triangles.
Area of the first unshaded triangle $=\dfrac{1}{2}(2)(4)=4\,cm^2$
Area of the second unshaded triangle $=\dfrac{1}{2}(2)(4)=4\,cm^2$
Area of the shaded triangle $=16-(4+4)=16-8=8\,cm^2$
Example 4
Examine the following diagram to work out the shaded triangle’s area.
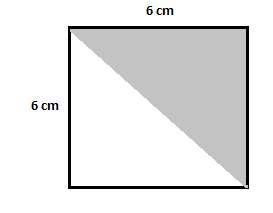
Solution
In the given diagram, the shaded triangle is present inside a square having the length of each side as $6\,cm$. In a similar manner as in the previous examples, let’s calculate the area of the square first:
Area of the square $=(6\,cm)^2=36\,cm^2$
Now calculate the area of the unshaded triangle:
Area of the unshaded triangle $=\dfrac{1}{2}\times 6\times 6=18\,cm^2$
Area of the shaded triangle $=36-18 = 18\,cm^2$
In this example, you can also observe that the area of the shaded and unshaded triangles is the same.
Example 5
Consider the rectangle below, and find the area of the shaded region.
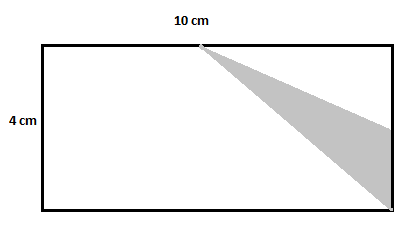
Solution
This figure has one bigger rectangle. To find the required area, you can see that there is one unshaded triangle. To simplify further, you just need to divide the figure into one more unshaded triangle and an unshaded rectangle as follows:
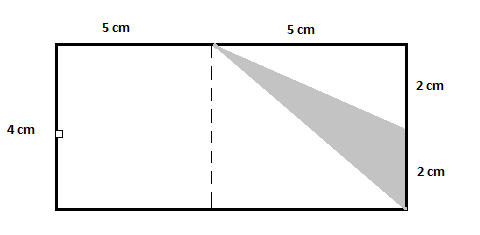
Now from the figure:
Area of the bigger rectangle $=10\times 4=40\,cm^2$
Area of the first unshaded triangle $=\dfrac{1}{2}\times 2\times 5=5\,cm^2$
Area of the second unshaded triangle $=\dfrac{1}{2}\times 5\times 4=10\,cm^2$
Area of the unshaded rectangle $=5\times 4=20\,cm^2$
Area of the shaded triangle $=40-(5+10+20) = 40-35=5\,cm^2$
What Is a Triangle?
A triangle is a three-sided polygon with three edges and vertices in geometry. The sum of a triangle’s internal angles equals 180 degrees, which is its most significant feature. This is also called the angle sum property of a triangle.
Principles
Some underlying principles, for instance, Pythagoras’ theorem and trigonometry, rely on triangle properties. Triangles are defined according to their angles and sides.
A triangle is a two-dimensional confined shape. It has three sides and is a polygon. Straight lines make up all of the sides. The vertex is the intersection of two straight lines. As a result, the triangle has three vertices.
Each vertex creates an angle. A triangle consists of three angles. When you extend the side length outwards, you get an exterior angle. The sum of a triangle’s subsequent interior and exterior angles is supplementary.
Types of Triangles
There are six basic types of triangles: scalene, isosceles, equilateral, acute angled, right angled, and obtuse angled. All of these triangle types are defined below.
1. Scalene Triangle: A scalene triangle is a triangle with three sides that have dissimilar side lengths. As a result, the three angles differ from one another.
2. Isosceles Triangle: The two sides of an isosceles triangle are equal in length. The two opposite angles to the two equal sides are also equal.
3. Equilateral Triangle: All three sides of an equilateral triangle are equal. As a result, all of the internal angles are of equal degrees, which means that each angle has a measure of 60 degrees.
4. Acute Angled Triangle: All of the angles in an acute triangle are less than 90 degrees.
5. Right Angled Triangle: The right-angled triangle has one angle with a measure of 90 degrees.
6. Obtuse Angled Triangle: Any one of the angles in an obtuse-angled triangle is greater than 90 degrees.
Area of the Triangle
The area of a triangle is the region that the triangle occupies in two-dimensional space. The areas of various triangles vary based on their dimensions. If the height and base length of a triangle is given, you can determine its area. It is expressed in square units.
If you are given a triangle with base $b$ and height $h$, then the area of the triangle is provided by a formula: $\dfrac{1}{2}\times base\times height$
With the aid of the following example, let us gain a better understanding of the area of a triangle.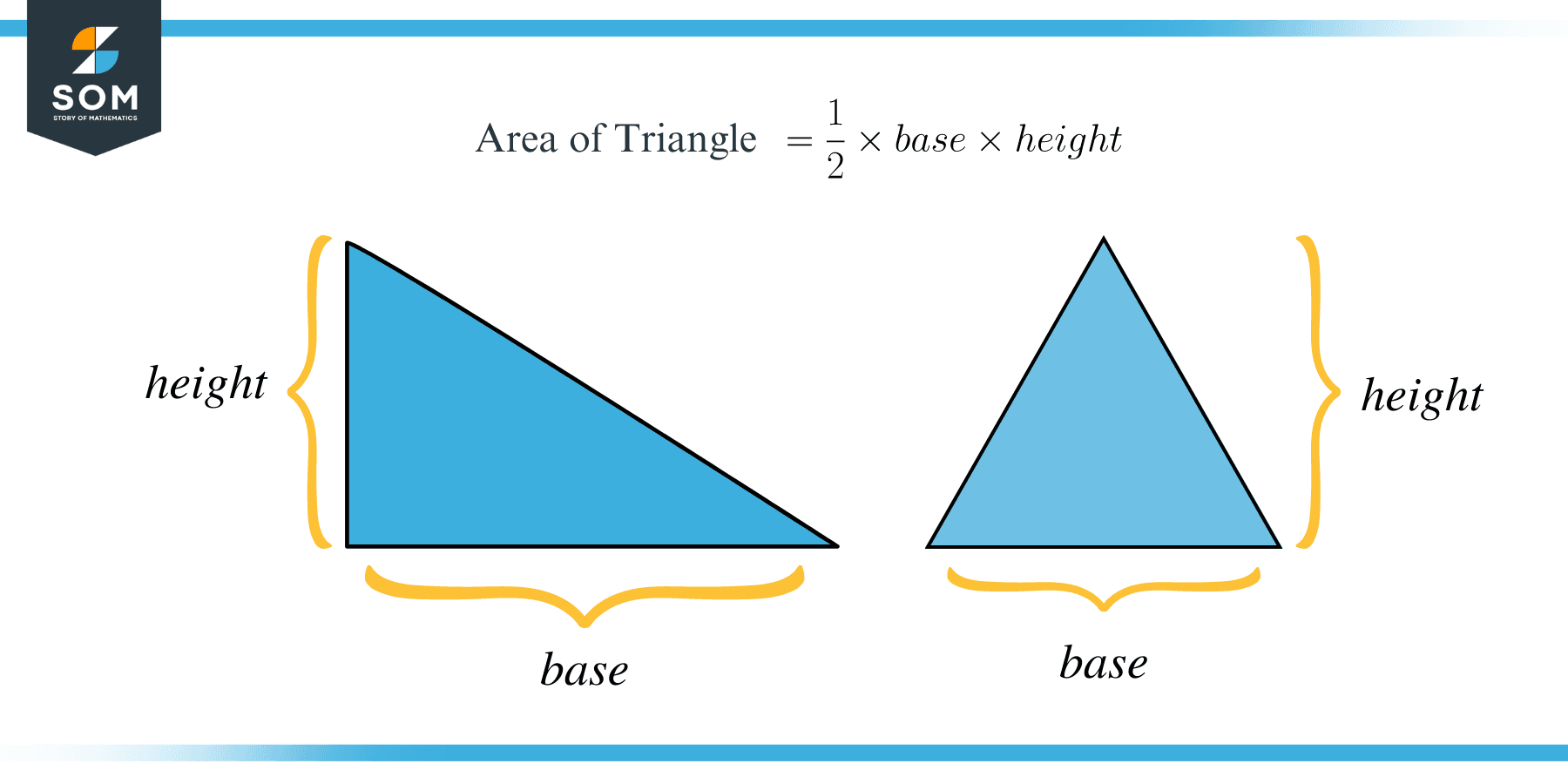
Example
Let $b=2cm$ and $h=3cm$ be the base and height of a triangle, respectively. Find its area.
Since the area of the triangle formula is $\dfrac{1}{2}\times base\times height$. Let $A$ be the area, you just need to plug in the values of base and height to find the area.
$A=\dfrac{1}{2}\times base\times height$
$A=\dfrac{1}{2}(2)(3)$
$A=3cm^2$
Heron’s Formula to Calculate the Area of a Triangle
Heron’s formula in geometry provides the area of a triangle whenever the measures of all three sides are given. In contrast to other triangle area formulae, it is not necessary to first calculate angles or other distances in the triangle. According to Heron’s formula, the area of a triangle with sides of lengths $a, b$, and $c$ is:
$A=\sqrt{s(s-a)(s-b)(s-c)}$
In this formula, $s$ is the semi-perimeter of the triangle such that:
$s=\dfrac{a+b+c}{2}$
Example
Work out the area of a triangle having sides of length $4,3$ and $5$ units length.
First, calculate $s$, that is, the semi-perimeter:
$s=\dfrac{a+b+c}{2}$ or $s=\dfrac{4+3+5}{2}=6$
Now, let $A$ be the area of the triangle, then:
$A=\sqrt{s(s-a)(s-b)(s-c)}$
$A=\sqrt{6(6-4)(6-3)(6-5)}$
$A=\sqrt{6(2)(3)(1)}$
$A=\sqrt{36}$
$A=6$ square units
Perimeter of a Triangle
The distance around any two-dimensional figure is classified as its perimeter. You can find the perimeter of every confined shape by adding the lengths of all of its sides. The perimeter of every polygon is the sum of the measure of its sides.
The perimeter refers to the sum of the three sides in the case of a triangle. When a triangle has three sides $a, b$, and $c$ and the perimeter is $P$, then mathematically, you can write:
$P=a+b+c$
Conclusion
This guide has provided a wealth of details on the shaded triangle’s area, so let us summarize the article for a better understanding of the entire study:
- A triangle is a three-edged polygon having three vertices.
- The most significant characteristic of a triangle is that the sum of its internal angles equals 180 degrees.
- There are six basic types of triangles.
- If the base length and height of a triangle are given, you can determine its area.
- The area of the triangle is the product of the length of base and height divided by $2$.
The area of the shaded triangle given inside any polygon can be calculated using the various formulae we have outlined in the guide above. You can solve some more examples in which you have to find out the area of the shaded triangle by dividing the given polygon into more sections. This way, you will have a vast knowledge of the formulas used for finding the areas of many different shapes in geometry.
