What Is the Derivative of Sec2x? A Detailed Guide

The derivative of $\sec2x$ is $2\sec2x\tan2x$. The chain rule is used to differentiate $\sec2x$. The chain rule comes up with a way to calculate the derivative of composite functions with both the number of functions in the composition identifying the number of differentiation steps required.

In this article, we will discuss in detail the methods involved in finding the derivative of $\sec2x$ as well as its second-order derivative.

What Is the Derivative of $\sec2x$?

The derivative of $\sec2x$ is $2\sec2x\tan2x$.

Let’s follow the steps in finding the derivative of $\sec2x$. To make it easier, suppose that $y=\sec2x$. The given function is in the form $y=f(g(x))$, where $g(x)=2x$ and $f(g(x))=\sec2x$. Next, differentiate both sides with respect to $x$ as follows:

$\dfrac{dy}{dx}=\dfrac{d}{dx}(\sec2x)$

The derivative of $\sec x$ is $\sec x\cdot \tan x$ and so you will get:

$y’=\sec2x\cdot\tan2x\cdot\dfrac{d}{dx}(2x)$

Again the derivative of $2x$ with respect to $x$ is $2$, so finally the result is: $y’=\sec2x\cdot\tan2x\cdot 2$ or $y’=2\sec2x\tan2x$.

Derivative of $\sec2x$ by First Principle

Let $f(x)$ be a function, then the derivative of $f(x)$ by the first principle can be worked out as:

$\dfrac{d}{dx}[f(x)]=\lim\limits_{h\to 0}\left[\dfrac{f(x+h)-f(x)}{h}\right]$

Here, $f(x)=\sec2x$ and so $f(x+h)=\sec[2(x+h)]$. Finally, by First Principle you can find the derivative of $\sec2x$ as follows:

$\dfrac{d}{dx}[\sec2x]=\lim\limits_{h\to 0}\left[\dfrac{\sec[2(x+h)]-\sec2x}{h}\right]$

It is well known that $\sec x=\dfrac{1}{\cos x}$ and so, $\sec 2x=\dfrac{1}{\cos 2x}$ and $\sec[2(x+h)]=\dfrac{1}{\cos [2(x+h)]}$.

$\dfrac{d}{dx}[\sec2x]=\lim\limits_{h\to 0}\dfrac{1}{h}\left[\dfrac{1}{\cos [2(x+h)]}-\dfrac{1}{\cos 2x}\right]$

$\dfrac{d}{dx}[\sec2x]=\lim\limits_{h\to 0}\dfrac{1}{h}\left[\dfrac{\cos2x-\cos [2(x+h)]}{\cos [2(x+h)]\cos 2x}\right]$

To further simplify the denominator, use the identity $\cos a-\cos b=-2\sin\left(\dfrac{a+b}{2}\right)\sin\left(\dfrac{a-b}{2}\right)$.

$\dfrac{d}{dx}[\sec2x]=\lim\limits_{h\to 0}\dfrac{1}{h}\left[\dfrac{-2\sin(-h)\sin (2x+h)}{\cos [2(x+h)]\cos 2x}\right]$

$\dfrac{d}{dx}[\sec2x]=2\lim\limits_{h\to 0}\left[\dfrac{\sin (2x+h)}{\cos [2(x+h)]\cos 2x}\right]\lim\limits_{h\to 0}\left[\dfrac{\sin h}{h}\right]$

Apply the limits:

$\dfrac{d}{dx}[\sec2x]=2\left[\dfrac{\sin (2x+0)}{\cos [2(x+0)]\cos 2x}\right](1)$

$\dfrac{d}{dx}[\sec2x]=2\left[\dfrac{1}{\cos 2x}\cdot\dfrac{\sin 2x}{\cos 2x}\right]$

$\dfrac{d}{dx}[\sec2x]=2\sec 2x\tan 2x$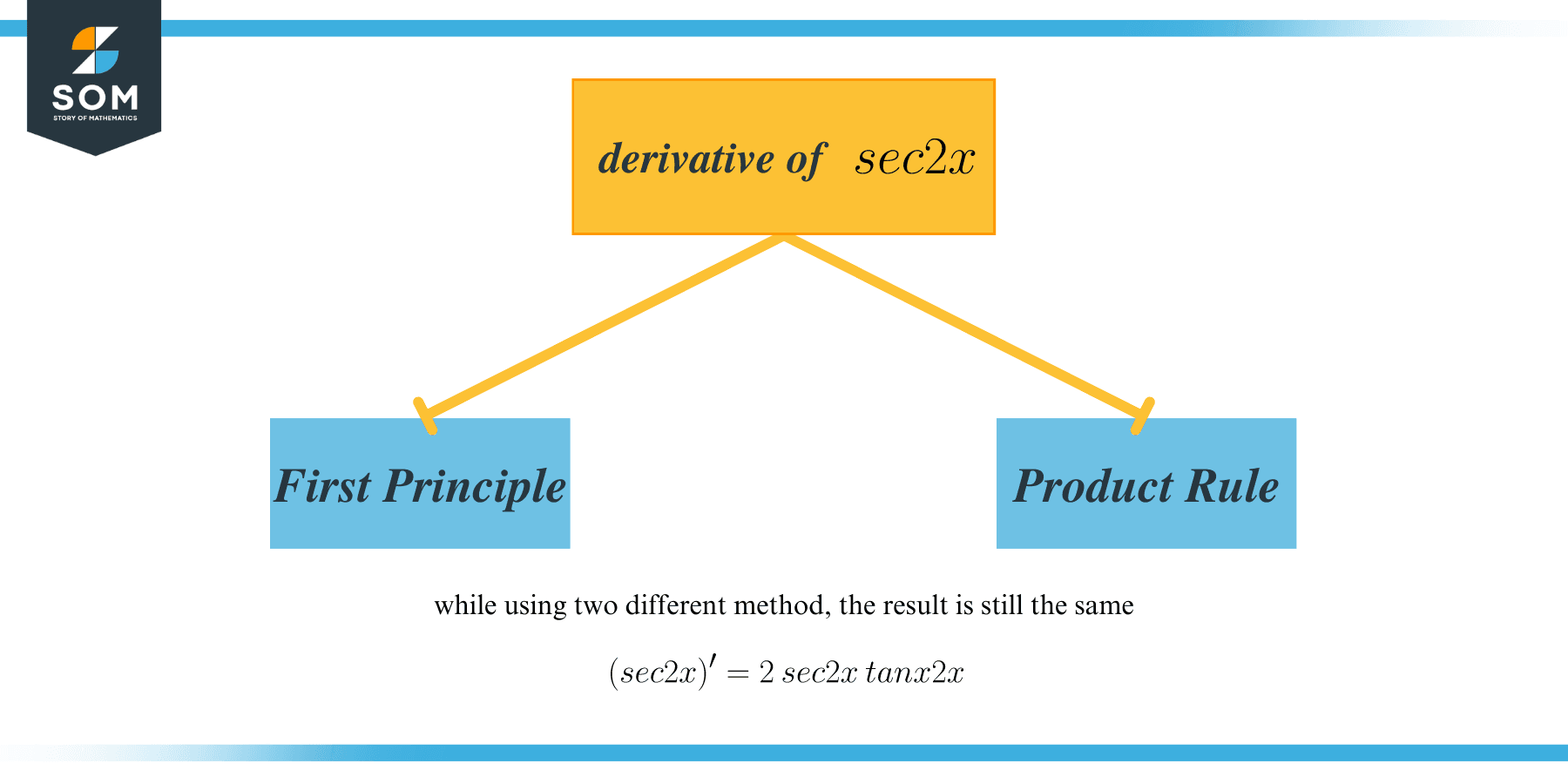

The Second Derivative of $\sec2x$

When you take the derivative of the derivative of a function, this is called the second derivative of that function. Though the first derivative indicates whether the function is decreasing or increasing, the second derivative indicates whether the first derivative is decreasing or increasing.

The positive second derivative indicates that the first derivative is increasing and the tangent line’s slope to the function increases with an increase in the value of $x.$ Similarly, if the second derivative is negative, the first derivative decreases, resulting in a decreasing tangent line’s slope to the function as $x$ increases.

To calculate the second derivative of a function, you just need to differentiate the first derivative. We know that the first derivative of $\sec 2x = 2\sec2x\tan2x$. So, to find the second derivative of $\sec2x$, just differentiate $2\sec2x\tan2x$. Since the second derivative will be the derivative of a function having the product of two terms, therefore, the product rule will be used to work out the second derivative in this case.

We have $y’=2\sec2x\tan2x$ so $y”=2\sec2x\dfrac{d}{dx}(\tan 2x)+2\tan 2x\dfrac{d}{dx}(\sec 2x)$ after the application of the product rule. Next, we know that the derivative of $\sec 2x$ is $2\sec 2x\tan2x$ and the derivative of $\tan 2x$ is $2\sec^2 2x$. So the substitution of these values in the above formula will give us:

$y”=2\sec2x(2\sec^2 2x)+2\tan 2x(2\sec 2x\tan 2x)$

$y”=4\sec^32x+4\sec 2x\tan^2 2x$

The Chain Rule

The chain rule is the method used to calculate the derivative of a composite function. It’s also known as the composite function rule. The chain rule only applies to composite functions.

Mathematically, let $f$ and $g$ be two differentiable functions. The derivative of the composition of these two functions can be expressed using the chain rule. To be more specific, if $y=f\circ g$ is the function in such a way that $y(x)=f(g(x))$ for every $x$, then the chain rule can be defined as $y'(x)=f'(g(x))g'(x)$.

The Secant Function

The secant of an angle in a right-angled triangle is the measure of the hypotenuse divided by the measurement of the adjacent side. It is abbreviated as “sec” when used in a formula. They are replaced easily by notations of the three more common types such as sin, cos, and tan.

$\sec x$ is referred to as the multiplicative inverse of the cosine function, so it exists specifically where $\cos x$ is not equivalent to $0$. Due to this fact, the domain of $\sec x$ contains all the real number excluding $\cdots ,-\dfrac{3\pi}{2},-\dfrac{\pi}{2},\dfrac{\pi}{2},\dfrac{3\pi}{2},\cdots$. $\sec x$ and $\tan x$ thus have identical domains. The range of $\sec x$ is significantly more complicated: keep in mind that the constraints on $\cos x$ are $−1 \leq \cos x \leq 1$.

So, if the secant of $x$ is positive, it cannot be less than one, and if it is negative, it cannot be greater than one. Hence, its range is divided into two intervals: $\sec x\geq 1$ and $\sec x\leq -1$. $\sec x$ has a similar period as $\cos x$, which implies that $\sec x$ has the period $2\pi$. $\sec x$ is an even function, which is due to $\cos x$ being an even function.

There exists an inverse function that works in opposite ways for every trigonometry function. These inverse functions share a similar name, but with the word “arc” before them. Therefore, the inverse of $\sec$ is $arc\sec$, and so on.

Conclusion

We now understand much more about the secant function and its first and second derivatives. To gain a better understanding of the derivative of $\sec 2x$, let us summarize the entire guide:

• $\sec x$ is the inverse function of $\cos x$.
• The derivative of $\sec 2x$ is $2\sec 2x\tan 2x$.
• The chain rule is employed to work out the derivative of the given function.
• The chain rule is used in finding the derivative of a composite function.
• The derivative of $\sec 2x$ can also be found using the First Principle.
• The second derivative of $\sec 2x$ involves the application of the product rule.

The derivative of $\sec 2x$ can be easily worked out using the chain rule, which is a convenient way to tackle the derivation of the composite functions. Why not take a few more functions such as $\sec 3x,\sec 4x$, and $\sec 5x$, and in a few steps, you’ll have slightly different values and a good command of carrying out the derivative of trigonometric functions!