Greatest Common Monomial Factor — Explanation and Examples

The greatest common monomial factor is the product of common factors of all the given monomials.

For example, if you are given three monomials, $6xy$, $4xy$ and $12xy$, then the product of common factors of each monomial will be called the G.C.F of the monomial.

The greatest common factor (G.C.F) is used in mathematics to find out the common denominators, and in real-life, G.C.F can be used in distribution scenarios. For example, you want to distribute some stuff among people, but you want all groups to have common distribution, and in such scenarios, you can use the concept of the G.C.F.

In this topic, we will discuss in detail what is meant by a polynomial, a monomial, G.C.F and how we find the G.C.F for given monomials.

What Is Greatest Common Monomial Factor?

The greatest common factor of a polynomial is the largest common factor which will divide each term of the polynomial, and each term of the polynomial is called a monomial; hence, it is called the greatest common factor of the monomial terms.

Factoring the G.C.F.

Below are the steps to factor out the greatest common factor of a polynomial.

1. Identify all the monomials and find out the prime factors for each monomial.
2. Find out the G.C.F of the given polynomial and write the polynomial as the product of G.C.F and the remaining factors.
3. Factor out the G.C.F by using the distributive property.

We will study how to identify a monomial further down this guide, and we will also discuss what is meant by the G.C.F and how you do factorization. There are certain steps to follow while doing the monomial factorization, and if you follow them, then you can easily apply them and solve for the G.C.F of monomials.

The factorization of the monomial can be done by following the steps listed below.

1. In the first step, separate the constant value from the variables.
2. In the second step, determine the prime factors of the constant value.
3. In the third step, determine the prime factors of the given variable.
4. In the last step, take the product of prime factors of constant value and the variable.

Once you have found out the factors of the monomial, then you can easily determine the G.C.F by simply taking the greatest or highest common factor and then factoring it out by using the distributive law. Let us now study the greatest common monomial factor examples with answers.

Example 1: What is the greatest common monomial factor of $6x+3$?

Solution:

The G.C.F for the given polynomial can easily be calculated by first identifying the factors of each term.

$6x = 3.2.x$

$3 = 3.1$

So the G.C.F for this polynomial is “$3$.”

$6x +3 = 3 (2x+1)$

Example 2: Determine the G.C.F from the monomials $6x^{2}$, $3x^{2}$ and $15x^{2}$.

Solution:

We know that the G.C.F will be an expression which divides each of the given monomials. Let us find out the prime factors of each monomial.

$6x^{2} = 3.2.x.x$

$3x^{2} = 3.x.x$

$15x^{2} = 3.5.x.x$

Most of the students ask the question “How did you find the greatest common monomial factor of the numerical coefficients of each term?” The answer is simple: by taking prime factors of the coefficient. We can see that the greatest common factor in each monomial is $= 3.2.x.x = 6x^{2}$.

As we are not dealing with a polynomial, hence we don’t need to factor out the G.C.F in this example.

Example 3: Determine the G.C.F and factor it out for the polynomial $16y^{2} – 8y$.

Solution:

Let us find out the prime factors for each term.

$16y^{2} = 2.2.2.2.y.y$

$8y = 2.2.2.y$

Now we can write them as:

$16y^{2} – 8y = (2.2.2.2.y.y) – (2.2.2.y)$

We can see that the common factor between these two is $2.2.2.y$, so factoring it out:

$16y^{2} – 8y = (2.2.2.y) (2.y-1) = 8y (2y-1)$

Here, $8y$ is the G.C.F for the given polynomial.

Example 4: Factor the given polynomial by finding the greatest common monomial factor.

$4y^{2} – 6y + 12$

Solution:

Let us find out the prime factors for each term.

$4y^{2} = 2.2.y.y$

$2y = 3.2.y$

$12 = 3.2.2$

We can see that the only common factor between all the terms is $2$, so it will also be the G.C.F. Factoring out the “$2$”, we get:

$4y^{2} – 6y + 12 = 2 ( 2y^{2} – 3y + 6)$

What Is G.C.F.?

G.C.F is the largest or highest number, and it is the factor of two or more numbers. When two or more numbers are given and we find out all the factors of the given numbers, then there will be a few factors that will be common, and if we take the product of such factors, then it will give us the G.C.F or highest common factor (H.C.F.).

Determining the G.C.F.

In Mathematics, factors are important in solving many problems. The G.C.F. can easily be determined by initially finding out the prime factors of given numbers and then just multiplying the factors which are common amongst them. For example, we are given two numbers, $16$ and $4$, and we want to find out the G.C.F. between these two numbers. Initially, we will find out the prime factors of each number.

The factors of the number $16$ are $1$,$2$,$4$, and $16$ because the number $16$ can be divided by these numbers.

The factors of $4$ are $1$, $2$, $3$, and $4$ because the number $4$ can be divided by these numbers.

Now the G.C.F, which can divide both $16$ and $4$, is “$4$”; hence the G.C.F. among these two numbers is $4$.

An alternative and mostly used method to calculate G.C.F. is by finding out the prime factors of both numbers. The goal of finding out the prime factors of any number or expression is to rewrite them in a simpler manner. For example, the prime factors of $16 = 2.2.2.2.1$ and the prime factors of $4 = 2.2.1$. As we can see, the common prime factors in both the numbers are “$2.2.1$”, and if we multiply them, then it will give us the G.C.F. So, the G.C.F. $= 2.2.1 = 4$. If we want to find the G.C.F between 18 and 30, then it can easily be found out as shown in the picture below.

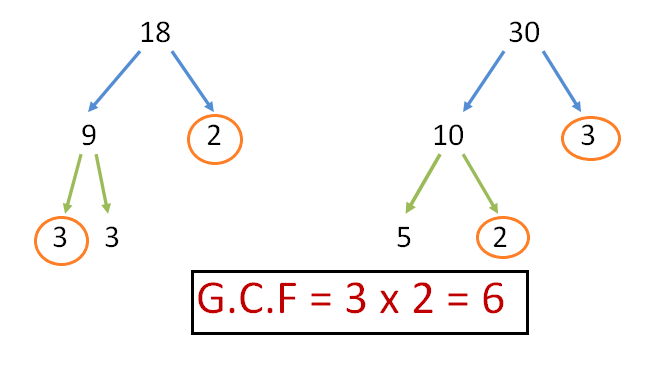
The process of factorization is essential to finding out the G.C.F. of polynomials or expressions because when you master the concept of factorization, then finding the factor of monomials and using them to find out the G.C.F. of a monomial will become much easier. So it is essential that before we move forward, you learn all you can regarding the concept of factorization here. (Link)

What Is a Monomial?

A monomial is a type of polynomial consisting of one term only. For example, single terms like $6x$, $5x^{2}$, and $4$ are called monomials. You have been solving mathematical problems involving monomials without even knowing that these are monomial expressions.

Identifying Monomials

Remember when you solved the problem “what is $1+1$ equal to?” this basically is an arithmetic expression that can also be called a binomial expression as it contains two terms, and we can say each individual term is a monomial term. Both the 1’s in this arithmetic expression are monomials, and the answer $2$ is also a monomial.

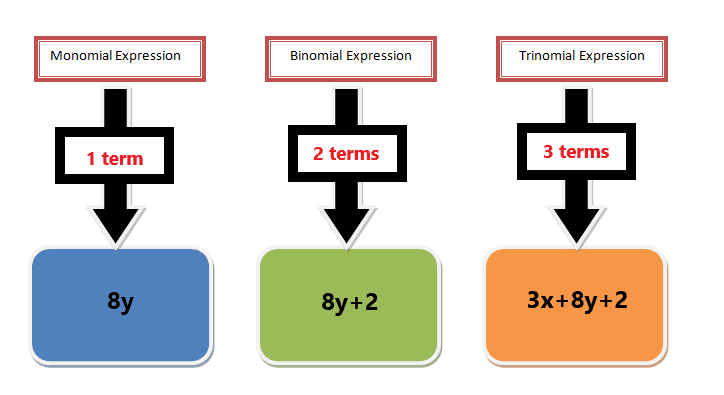
You must learn to identify a monomial before solving the problems related to the greatest common monomials factor. A monomial term can be a constant or a single variable, but any single variable which has a negative or fraction exponent will not be considered a monomial.

Monomial terms are also part of a polynomial expression. A polynomial expression can be a combination of several terms separated by signs of addition and subtraction. For example, the polynomial expression $3x^{2}+ 6x + 5$ is a trinomial expression with three terms, but if we take each term individually, then each term will be called a monomial. In this example, the terms $3x^{2}$, $6x$, and $5$ are all monomial, and if we factorize each term, then it will be called monomial factorization. Furthermore, if we take the common prime factors among each term and then factor out the G.C.F, it will be called the greatest common-monomial – factor.

Let us study the rules which are followed by the monomials.

1. When we multiply a monomial with a constant number, then the product will yield a monomial term. For example, if we are given a monomial expression “$3x$” and multiply it by a constant number of $5$, then the result will be $15x$, which is also a monomial term. Similarly, if we multiply the number $20$ with the number $10$, then the result will be $200$, and in this case, both $20$ and $200$ are monomial terms.
2. When we multiply two monomial variables, then the result will also be a monomial variable. For example, if we multiply $5x$ with variable $4x$, the resulting variable will be $20x^{2}$, and in this example, all the three variables $5x$,$4x$ and $20x^{2}$ are monomials. Similarly, if we multiply $5xy$ with $6xy$, then the resulting term will be $30x^{2}y^{2}$, and in this example, all the three terms $5xy$, $6xy$ and $30x^{2}y^{2}$ are monomials.
3. When two monomials are separated by an addition or subtraction sign, then the expression will not be called a monomial unless both terms have the same variables. For example, if we were given an expression “$4x+6y$”, then it will be called a binomial expression, and similarly, if three monomials are separated by addition or subtraction signs, for example, the expression $4x +6y +7$ will be called a trinomial expression. But if the expression with two or more terms contains the same variable, for example, the expression $4x+6x$ can be written as $10x$; hence, such expressions are called monomials. 
4. When we divide a monomial by another monomial, then the resulting expression will only be called a monomial if it does not have a negative or fraction exponent. For example, if we divide a monomial $6x^{2}$ by $3x^{2}$, then the result is $2$, which is a monomial, but if a monomial is $5x^{2}$ and it is divided by $5x^{4}$, then the result is $x^{-2}$ or $x^{\dfrac{1}{2}}$, and this is not a polynomial. Hence, the expression $\dfrac{6x^{2}}{3x^{2}}$ will be called a monomial expression, while the expression $\dfrac{5x^{2}}{5x^{4}}$ will not be called a monomial expression.

We have now studied in detail what a monomial is and its properties. Now let us study some examples to firmly revise what we have learned related to the identification of monomials so that when you are dealing with a complex expression, you can identify which is a monomial expression.

Example 5: Identify which of the expressions listed below is a monomial expression.

1. $3x + 4y$
2. $6y + 2x$
3. $8y^{3}$
4. $\dfrac{6xy}{3x}$
5. $5y \times 6x$

Solution:

1. The expression contains two terms $3x$ and $4y$ with different variables which are separated by an addition sign; hence it is a binomial expression, not a monomial expression.
2. The expression contains two terms $6y$ and $2x$ with different variables which are separated by an addition sign; hence it is a binomial expression, not a monomial expression.
3. $6x^{3}$ is a monomial expression.
4. We are given a fraction $\dfrac{6xy}{3x}$, and if we divide them, the final result is $2y$, hence the expression is a monomial expression.
5. We are given a product of two monomials, and we know that when a monomial is multiplied by another monomial, the result is always a monomial.

Example 6: Identify which of the following expressions are monomial:

1. $10x – 5y$
2. $6 (11x – 5xy)$
3. $7y^{3} – 6y^{3}$
4. $\dfrac{10}{2}$
5. $5x^{2} \times (6x + 3)$

Solution:

1. The expression contains two terms $10x$ and $5y$ with different variables which are separated by a subtraction sign; hence it is a binomial expression, not a monomial expression.
2. In this expression, we are multiplying the constant number 6 with a binomial expression; hence the expression is not a monomial expression.
3. The expression $7y^{3} – 6y^{3}$ can be written as $y^{3}$; hence it is a monomial expression as both terms have the same variable.
4. The fraction $\dfrac{10}{2}$ is equal to $5$; hence it is a monomial expression.
5. In this expression, we are multiplying $5x^{2}$ with a binomial expression; hence this expression is not a monomial expression.

Practice Questions

1. Determine the G.C.F. and factor it out for the polynomial $25xy^{3}z^{2} – 15xyz + 75 x^{2}y^{2}z$.
2. Determine the G.C.F. and factor it out for the polynomial $-4y^{2} + 6y + 18$.
3. Determine the G.C.F. and factor it out for the polynomial $-8xy^{2} – 12xy + 18x^{2}y$.

Answer Key

1).

Let us find out the prime factors for each monomial term

$25xy^{3}z^{2}= 5.5.x.y.y.y.z.z$

$15xyz = 5.3.x.y.z$

$75x^{2}y^{2}z= 5.5.3.x.x.y.y.z$

The common prime factor among these terms is $5.x.y.z$, so factoring it out, we get:

$25xy^{3}z^{2} – 15xyz + 75 x^{2}y^{2}z = 5xyz (5y^{2}z – 3 + 15xy)$

Hence, $5xy$ is the G.C.F. for the given polynomial.

2).

When we are given a polynomial such that the first term is negative, then we change the sign of the common factor, and then we factor that out.

Let us find out the prime factors for each term.

$-4y^{2}= -1.2.2.y.y$

$ 6y = 3.2.y $

$18 = 3.3.2$

The G.C.F. is “$2$”, but as the first term of the polynomial is negative, we will factor out the G.C.F. with the opposite sign, which is “$-2$.”

$-4y^{2} + 6y + 18 = -2 ( 2y – 3y – 9)$

3).

As the first term of the polynomial is negative, we will change the sign of the G.C.F. calculated for this polynomial.

Let us find out the prime factors for each term.

$-8xy^{2}= -1.2.2.2.x.y.y$

$ 12xy = 3.2.2.x.y $

$18x^{2}y = 3.3.2.x.x.y$

The common factor among all monomials is $2.x.y$, so the G.C.F is 2xy, but as the first term of the polynomial is negative, we will factor out the G.C.F. with the opposite sign that is “$-2xy$”.

$-8xy^{2} – 12xy + 18x^{2}y = -2xy (4y + 6 – 9x)$