JUMP TO TOPIC
 A matrix that consists of the coefficients of a linear equation is known as a coefficient matrix.
A matrix that consists of the coefficients of a linear equation is known as a coefficient matrix.
The coefficient matrix solves linear systems or linear algebra problems involving linear expressions. In the study of matrices, the coefficient matrix is used for arithmetic operations on matrices. A method like Cramer’s rule utilizes coefficient matrices to find the unknown values of a linear equation.
In this guide, we will learn how to develop a coefficient matrix from a given set of linear equations. Furthermore, we will study applications of coefficient matrix by solving numerical examples.
What Is Coefficient Matrix?
The matrix used to represent the coefficients of the variables of a linear equation is called a coefficient matrix. For example, we have two linear equations:
A: $3x + 4y = 2$
B: $6x + 9y = 1$
In these linear equations, the coefficients of the variable “$x$” are $3$ and $6$, while the coefficients of the variable “$y$” are $4$ and $9$.
How To Write a Coefficient Matrix
Writing a developing a coefficient matrix from a linear equation is very easy. If we write the coefficients of the above example in matrix form, then the corresponding matrix will be:
$\begin{bmatrix}3 & 4 \\ 6 & 9 \end{bmatrix}$
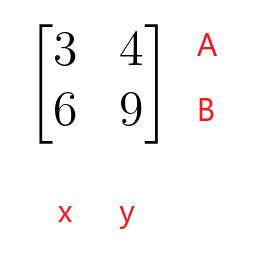
The first row of the coefficient matrix represents row A of the linear equation and the second row of the coefficient matrix represents row B of the linear equation. The first column of the coefficient matrix represents the coefficients of the “$x$” variable, while the second column of the coefficient matrix represents the coefficients of the “$y$” variable. The coefficient matrix doesn’t need to be a square matrix as it can take the shape of a rectangular, column, or row matrix as well.
The question which may arise in your mind is, “What about the other elements of the linear equation?” The matrix of variables “$x$” and “$y$” is known as the variable matrix, while the matrix of constant terms “$2$” and “$1$” is known as the constant matrix.
Coefficient Matrix Vs Augmented Matrix
The augmented matrix, just like the coefficient matrix, includes the coefficients of a linear equation in matrix form. As the name suggests, these coefficients are then combined with the column of another matrix to form an augmented matrix. For example, we have a set of linear equations:
$3x +5y -2z = 6$
$5x -6y +8z = 1$
$4x +2y -3z = -2$
We can write the coefficient matrix for above given linear equations as:
$A = \begin{bmatrix}3 & 5 & -2 \\ 5 & -6 & 8 \\ 4 & 2 & -3 \end{bmatrix}$
Suppose the constant matrix is B and is given as:
$B = \begin{bmatrix}6 \\ 1 \\ -2 \end{bmatrix}$
Now, if we combine the column of the B matrix with the columns of the A matrix, then we will get an augmented matrix C.
$\begin{bmatrix} 3 & 5 & -2 &\bigm| & 6 \\ 5 & -6 & 8 &\bigm| & 1 \\4 & 2 & -3 &\bigm|&-2\end{bmatrix}$
Let us now study coefficient matrix examples.
Example 1: Write down the coefficient matrix for the given set of linear equations
$ x – 2y = 0 $
$ 4x – 4y = 2 $
Solution:
1).
We can write the coefficient matrix for the given set of linear equations as:
$\begin{bmatrix}1 & -2 \\ 4 & -4 \end{bmatrix}$
Example 2: Write down the coefficient matrix for the given set of linear equations.
$ x – 3z = 0 $
$ 4y – 2z = -2 $
Solution:
1).
We can write the coefficient matrix for the given set of linear equations as:
$\begin{bmatrix}1 & 0 & -3 \\ 0 & 4 & -2 \end{bmatrix}$
Example 3: Write down the coefficient matrix for the given set of linear equations.
$ x – 2y + 5z = 4 $
$ 4x – 7z = 0 $
$ 6x – 9y – 5z = 1 $
Solution:
1).
We can write the coefficient matrix for the given set of linear equations as:
$A = \begin{bmatrix}1 & -2 & 5 \\ 4 & 0 & -7 \\ 6 & -9 & -5 \end{bmatrix}$
Example 4: Adam got a job in a multinational company. He was given a good salary package with annual increments. Adam’s monthly salary after completing $3$ years of service was $32,000$ dollars, and his monthly salary after completing $7$ years of service was $52,000$ dollars. Write down the linear equations relating the salary “$x$” and the annual increment “$y$” and find out the coefficient matrix.
Solution:
We can write the linear equations for the given problem as follows:
$x + 3y = 32,000$
$x + 7y = 52,000$
We can write the coefficient matrix for a given set of linear equations as:
$A = \begin{bmatrix}1 & 3 \\ 1 & 7 \end{bmatrix}$
Coefficient Matrix Applications
We can use the coefficient matrix to determine the values of variables of linear equations. Linear equations arise in many important engineering problems. Sometimes, the number of simultaneous equations is so large that we rely on computer tools to find the solutions. You will often hear the terms coefficient matrix Matlab and coefficient matrix Python. So, in general, coefficient matrices are used in various fields.
Our main focus is the usage of coefficient matrix to solve linear equations. The coefficient matrix can be used in a conventional method. For example, if we are given two sets of linear equations:
$4x + 2y = 2$
$6x – 4y = 5$
$\begin{bmatrix}4 & 2 \\ 6 & -4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 \\ 5 \end{bmatrix}$
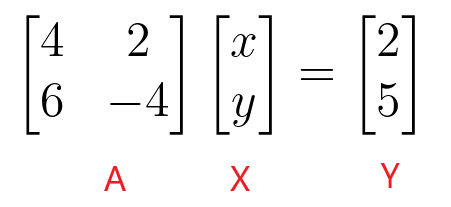
We can find the values of “$x$” and “$y$” by taking the inverse of the coefficient matrix and then multiplying it with the constant matrix.
Similarly, the values of “$x$” and “$y” can also be found using Cramer’s rule. We can say that coefficient matrices are used to solve for:
- Transpose of matrix
- Determinant of matrix
- To solve linear Equations
- To find out the Eigen Values of linear equations
In this topic, we will only study how coefficient matrices are used to solve the value “$x$” and “$y$” of linear equations using a simple inverse method.
Coefficient Matrix Inverse
The coefficient matrix formula for calculation of the inverse of the matrix is given as:
$A^{-1} = \dfrac{Adj A}{ Det A}$
Here, “Adj” is the adjoint of a matrix while “Det” is the determinant of a matrix.
Example 5: Determine the coefficient matrix for a given set of linear equations and then solve the equations using the inverse of the coefficient matrix.
$ x + 3y = 2 $
$ 2x – 6y = 4 $
Solution:
We can write the coefficient matrix for a given set of linear equations as:
$\begin{bmatrix}1 & 3 \\ 2 & -6 \end{bmatrix}$
We can write the linear equations in matrices form as:
$\begin{bmatrix} 1 & 3 \\ 2 & -6 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \end{bmatrix}$
$A.X = B$
$X = A^{-1}.B$
$A^{-1} = \dfrac{Adj A}{ Det A}$
$Adj A = \begin{bmatrix} -6 & -3 \\ -2 & 1 \end{bmatrix}$
$Det A = \begin{vmatrix} 1 & 3 \\ 2 & -6 \end{vmatrix}$
$Det A = -6 – 6 = -12$
$A^{-1} = \dfrac{\begin{bmatrix} -6 & -3 \\ -2 & 1 \end{bmatrix}}{-12 }$
$A^{-1} = \begin{bmatrix} \dfrac{1}{2} & \dfrac{1}{4} \\ \\ \dfrac{1}{6} & -\dfrac{1}{12} \end{bmatrix}$
$X = \begin{bmatrix} \dfrac{1}{2} & \dfrac{1}{4} \\ \\ \dfrac{1}{6} & -\dfrac{1}{12} \end{bmatrix}\begin{bmatrix} 2 \\ 4 \end{bmatrix}$
$X = \begin{bmatrix} 1 + 1 \\ \\ \dfrac{1}{3} – \dfrac{1}{3} \end{bmatrix}$
$X = \begin{bmatrix} 2 \\ 0 \end{bmatrix}$
Hence $x = 2$ and $y = 0$
Example 6: Determine the coefficient matrix for a given set of linear equations and then solve the equations using the inverse of the coefficient matrix
$ 3x + 4y = 2 $
$ 2x + 6y = 5 $
Solution:
We can write the coefficient matrix for a given set of linear equations as:
$\begin{bmatrix}3 & 4 \\ 2 & 6 \end{bmatrix}$.
We can write the linear equations in matrices form as:
$\begin{bmatrix} 3 & 4 \\ 2 & 6 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 \\ 5 \end{bmatrix}$
$A.X = B$
$X = A^{-1}.B$
$A^{-1} = \dfrac{Adj A}{ Det A}$
$Adj A = \begin{bmatrix} 6 & -4 \\ -2 & 3 \end{bmatrix}$
$Det A = \begin{vmatrix} 3 & 4 \\ 2 & 6 \end{vmatrix}$
$Det A = 18 – 8 = 10$
$A^{-1} = -\dfrac{\begin{bmatrix} 6 & -4 \\ -2 & 3 \end{bmatrix}}{10}$
$A^{-1} = \begin{bmatrix} \dfrac{3}{5} & -\dfrac{2}{5} \\ \\ -\dfrac{1}{5} & \dfrac{3}{10} \end{bmatrix}$
$X = \begin{bmatrix} \dfrac{3}{5} & -\dfrac{2}{5} \\ \\ -\dfrac{1}{5} & \dfrac{3}{10} \end{bmatrix} \begin{bmatrix} 2 \\ 5 \end{bmatrix}$
$X = \begin{bmatrix} \dfrac{6}{5} – 2 \\ \\ -\dfrac{2}{5} + \dfrac{3}{2} \end{bmatrix}$
$X = \begin{bmatrix} -\dfrac{4}{5} \\ \dfrac{11}{10} \end{bmatrix}$
Hence $x = -\dfrac{4}{5}$ and $y = \dfrac{11}{10}$
Example 7: Take example no.4 and calculate Adam’s initial salary and the annual increment.
Solution:
We know the linear equations for the given problem are:
$x + 3y = 30,000$
$x + 7y = 50,000$
$\begin{bmatrix} 1 & 3 \\ 1 & 7 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 30,000 \\ 50,000 \end{bmatrix}$
$A.X = B$
$X = A^{-1}.B$
$A^{-1} = \dfrac{Adj A}{ Det A}$
$Adj A = \begin{bmatrix} 7 & -3 \\ -1 & 1 \end{bmatrix}$
$Det A = \begin{vmatrix} 1 & 3 \\ 1 & 7 \end{vmatrix}$
$Det A = 7 – 3 = 4$
$A^{-1} = -\dfrac{\begin{bmatrix} 7 & -3 \\ -1 & 1 \end{bmatrix}}{2 }$
$A^{-1} = \begin{bmatrix} \dfrac{7}{4} & -\dfrac{3}{4} \\ \\ -\dfrac{1}{4} & \dfrac{1}{4} \end{bmatrix}$
$X = \begin{bmatrix} \dfrac{7}{4} & -\dfrac{3}{4} \\ \\ -\dfrac{1}{4} & \dfrac{1}{4} \end{bmatrix} \begin{bmatrix} 32,000 \\ 52,000 \end{bmatrix}$
$X = \begin{bmatrix} 56000 – 39000 \\ \\ -8000 + 13000 \end{bmatrix}$
$X = \begin{bmatrix} 17000 \\ 5000 \end{bmatrix}$
Hence, the initial salary of Adam was $17000$ dollars, and his job’s annual increment is $5000$ dollars.
Practice Questions
1. Write down the coefficient matrix for the given set of linear equations.
$ x – 2y = 4 $
$ – 5z = 0 $
$ 2x – 5z = 1 $
2. Determine the coefficient matrix for a given set of linear equations and then solve the equations using the inverse of the coefficient matrix.
$ 8x – 4y = 16 $
$ 6x + 5y = 32 $
Answer Key:
1).
We can write the coefficient matrix for the given set of linear equations as:
$A = \begin{bmatrix}1 & -2 & 0\\ 0 & 0 & -5 \\ 2 & 0 & -5 \end{bmatrix}$
2).
We can write the coefficient matrix for the given set of linear equations as:
$\begin{bmatrix}8 & -4 \\ 6 & 5 \end{bmatrix}$
We can write the linear equations in matrices form as:
$\begin{bmatrix} 8 & -4 \\ 6 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 16 \\ 32 \end{bmatrix}$
$A.X = B$
$X = A^{-1}.B$
$A^{-1} = \dfrac{Adj A}{ Det A}$
$Adj A = \begin{bmatrix} 5 & 4 \\ -6 & 8 \end{bmatrix}$
$Det A = \begin{vmatrix} 8 & -4 \\ 6 & 5 \end{vmatrix}$
$Det A = 40 + 24 = 64$
$A^{-1} = -\dfrac{\begin{bmatrix} 1 & 3 \\ 2 & -6 \end{bmatrix}}{64 }$
$A^{-1} = \begin{bmatrix} \dfrac{5}{64} & \dfrac{1}{16} \\ \\ -\dfrac{3}{32} & \dfrac{1}{8} \end{bmatrix}$
$X = \begin{bmatrix} \dfrac{5}{64} & \dfrac{1}{16} \\ \\ -\dfrac{3}{32} & \dfrac{1}{8} \end{bmatrix} \begin{bmatrix} 16 \\ 32 \end{bmatrix}$
$X = \begin{bmatrix} \dfrac{5}{4} + 2 \\ \\ -\dfrac{3}{2} + 4 \end{bmatrix}$
$X = \begin{bmatrix} \dfrac{13}{4} \\ \dfrac{5}{2} \end{bmatrix}$
Hence, $x = \dfrac{13}{4}$ and $y = \dfrac{5}{2}$
