Factoring Monomials — Explanation and Examples

The term factoring monomials mean to factorize a monomial into a product of two or more monomials.

In this complete guide, we will discuss in detail what a monomial means and how we factorize a monomial, along with related examples.

What Is Factoring Monomials?

The term factoring a monomial means that we break down the given monomial into products of its prime factors, and we can call them factor monomials. For a given monomial, during its factorization, we have to find the prime factors of the constant and the variable.

Examples

For example, if we are given a monomial $6x^{3}$, then we will have to find the prime factors of constant 6 as well as the prime factors of $x^{3}$. So if we want to write factors of the monomial $6x^{3}$, then we will first write down the prime factors of $6$, which are $(3) (2) (1)$. Similarly, in the next step, we will find prime factors of $x^{3}$, which can be written as $x.x.x$. So the complete factors of the monomial $6x^{3}$ are $3.2.x.x.x$.

You need to follow the steps given below for factoring a monomial:

1. The first step is the identification of a monomial. In this step, you first identify whether or not the given expression is a monomial.

2. In the second step, you will separate the constant term from the variable term.

3. In the third step, you will find out the prime factors of the constant.

4. In the fourth step, you will find out the prime factors of the variable.

5. In the last step, you multiply all the factors which you found out in the third and fourth steps, and it will give the original monomial.

Let us now study some factoring monomials examples.

Example 1: Find the factors for the monomial $8x^{6}$.

Solution:

Let us first find out the prime factors of constant $8$.

$8 = 4.2 = 2.2.2$

The prime factors of $x^{6}$ will be:

$x^{6} = x.x.x.x.x.x$

$8x^{6} = 2.2.2.x.x.x.x.x.x$

Example 2: Find the factors for the monomial $8x^{3}y^{4}$.

Solution:

Let us first find out the prime factors of constant $8$.

$8 = 4.2 = 2.2.2$

The prime factors of $x^{6}$ will be:

$x^{3} = x.x.x$

$y^{4} = y.y.y.y$

$8x^{3}y^{4} = 2.2.2.x.x.x.y.y.y.y$

Example 3: Find the factors for the monomial $6x^{5} + 10 x^{5}$.

Solution:

First of all, add up the given terms:

$6x^{5} + 10 x^{5} = 16x^{5}$

Prime factors of constant 16 are:

$16 = 4.4 = 2.2.2.2$

Prime factors of $x^{5}$:

$x^{5} = x.x.x.x.x$

$16x^{5} = 2.2.2.2.x.x.x.x.x$

Example 4: Find the value of “$k$” for the given expression $16x^{5} = 4x^{3}. k$.

Solution:

We can find the value of “$k$” by completing the factorization of the given polynomial, or we can simply divide both sides by $4x^{3}$.

Dividing both sides by $4x^{3}$:

$\dfrac{16x^{5}}{4x^{3}} = \dfrac{4x^{3}.k}{4x^{3}}$

$4x^{2} = k$

We can verify that k is a monomial factor of $16x^{5}$ because if we multiply it by $4x^{3}$, it gives us the original monomial expression.

Factoring Monomials and Greatest Common Factor

Factoring a monomial is essential to determine the greatest common factor or G.C.F of given monomials. For example, we are given three monomials $8x^{2}y$, $16x^{2}y$, and $32xy$, and we want to find the G.C.F. We can do that by factoring each monomial and taking the product of the common factors.

Now let us find the prime factors of monomials $8x^{2}y$, $16x^{2}y$, and $32xy$.

$8x^{2}y = 2.2.2.x.x.y$

$16x^{2}y = 2.2.2.2.x.x.y$

$32xy = 2.2.2.2.2.x.y$

We can see that the common prime factors in each monomial are $2,2,2,x$ and $y$. If we multiply all these common factors, then it will give us the G.C.F. Hence, the G.C.F in this case will be:

G.C.F = $2.2.2.x.y = 8xy$

Factoring Monomials From Polynomials

We can factor a monomial from a polynomial expression. To factor a monomial term from a polynomial, we follow the steps listed below.

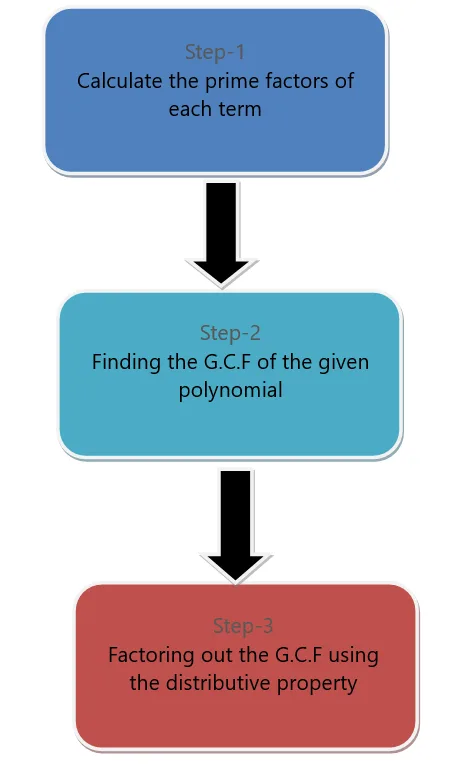
For example, we want to factorize the polynomial $6x^{2} + 9x^{4}$ through factoring monomials.

First of all, we factorize each term.

$6x^{2} = 3.2.x.x$

$9x^{4} = 3.3.x.x.x.x$

The common factor among these terms is $3$,$x$, and $x$. So the G.C.F is equal to $3x^{2}$. Now factor out the G.C.F, then the final expression will be:

$3x^{2} (2+3x^{2})$.

What Is a Monomial?

A monomial is a type of polynomial with a single expression. The word monomial is a combination of two words, “Mono” and “Mial”; “Mono” means one while “Mial” means a term, so it means a single term.

Examples

For example, if we are given a polynomial $3x^{2}- 4x + 5$, then we can say that this polynomial is a combination of three monomials. Here, $3x^{2}$, $4x$ and $5$, each expression is a monomial. A monomial can never have a negative or fraction exponent. For example, if we are given an expression $3x^{-3}$ or $3\sqrt{x}$, then both of these expressions are not monomials.

In elementary school, when you started working with arithmetic operations, the first addition problem you solved was most likely $1+1 = 2$. Now can you guess the number of monomials in the expression $1 + 1 = 2$? As you can see, the expression contains only constants and constants are also considered monomials, so in this expression, both 1’s and $2$ are monomials. So you have been working with monomials since your early school days.

A monomial can be a single variable or a constant. Similarly, it can also be the product of variables and constants, but if an expression contains an addition or subtraction sign which separates two or more algebraic expressions, then such an expression will be termed a polynomial. So we can say that a polynomial is formed by the combination of two or more monomials. For example, $2x^{2}$, $-5$, and $6y$ all three expressions are monomials, but if we combine them and write them as $2x^{2}+6y – 5$, then this whole expression will be called a polynomial.

Rules

A monomial follows some rules, which are:

1. When a monomial is multiplied with a constant value, the result will also be a monomial. For example, if we are given a monomial $4x$,and we multiply it by $4$, the result will be $4 \times 4x = 16x$, which is also a monomial. Similarly, if we give a constant value of $5$ and we multiply it by $10$, the result will be a constant value of $50$, which is also a monomial.

2. When a monomial containing a variable is multiplied by another monomial containing a variable, the result will also be a monomial. For example, if we are given a monomial $4x^{2}$ and we multiply it by $3x^{2}$, then the result will be $4x^{2} \times 3x^{2} = 12 x^{4}$, which is also a monomial. Similarly, if we multiply $3x$ with $4y$, then the result will be $12xy$, which is also a monomial.

3. If two or more terms are separated by an addition or subtraction sign, then it will not be called a monomial. For example, if we are given an expression $3x + 4y$ or $3x – 5$, then both these expressions are not monomials. But if we are given an expression having two or more terms but all the terms contain with same variable and exponential power, then it will be a monomial. For example, the expression $3x^{2}+ x^{2} -2x^{2}$ can be written as $2x^{2}$; hence it will be called a monomial.

4. When a monomial is divided by another monomial, then the result will be a monomial if and only if the exponent of the resultant expression is not negative. For example, if we divide $4x^{2}$ by $2x$, then the result will be $2x$, which is a monomial, and similarly, if we divide $4x^{2}$ by $4x^{3}$, then the result will be $x^{-1}$ or $\dfrac{1}{x}$, which is not a monomial.

Let us study some examples regarding the identification of a monomial.

Example 5: Identify which of the following expressions are monomials:

1. $2x + 3y$
2. $2x + 5x$
3. $5x^{3}$
4. $\dfrac{6x}{3x}$
5. $\dfrac{5x^{4}}{6x^{5}}$

Solution:

1. The expression contains two terms; hence it is a binomial expression and it is not a monomial expression.
2. The expression $2x + 5x$ can be added up, and the final result is $7x$; hence it is a monomial.
3. $5x^{3}$ is a monomial.
4. The final result of the expression $\dfrac{6x}{3x}$ is equal to $2$, hence it is a monomial.
5. The expression $\dfrac{5x^{4}}{6x^{5}}$ result will contain a negative exponent, and hence it is not a monomial.

Example 6: Identify which of the following expressions are monomials:

1. $2x – 3y$
2. $6 (3x+5x)$
3. $5x^{3} – 3x^{3}$
4. $\dfrac{6}{3}$
5. $5x \times 6x$

Solution:

1. The expression contains two terms; hence it is a binomial expression, and it is not a monomial expression.
2. The expression $6 (3x+5x)$ can be written as $6 (3x+5x) = 6 \times 8x = 48x$, hence it is a monomial.
3. The expression $5x^{3} – 3x^{3}$ can be written as $2x^{3}$, so it is a monomial.
4. The fraction $\dfrac{6}{3}$ can be written as $18$, hence it is a monomial.
5. The expression $5x \times 6x$ can be written as $30x^{2}$; hence it is a monomial.

Factoring or Factorization

The term factoring or factorization in mathematics means the decomposition of an expression into a product of smaller expressions, which, when multiplied, will give the original expression. For example, if we are given a constant number $21$, we can write it as a product of $7$ and $3$ ( $21 = 7 \times 3$). In this case, $7$ and $3$ are called prime factors of the number $21$.

Factoring polynomials can contain monomials, binomials or trinomials. For example, if we are given a binomial expression $x^{2} – 9$, then it can be written as the product of $(x-3) (x+3)$.

The aim of factoring any expression is to write it in a simpler manner or to determine its roots or prime factors. In the case of a monomial, the factoring is done to reduce it to other monomials. It is used as a building block to learning the process of factorization, and when you master factoring monomials, then you can easily tackle advanced problems related to the factorization of a polynomial.

Practice Questions

1. Factorize the monomial $16x^{6}y^{3}$.
2. Calculate the G.C.F. among the terms $64x^{3}y$, $44 xy^{2}$ and $36x^{2}y^{2}$ by using monomial factorization.

Answer Key:

1).

$16x^{6}y^{3} = 2.2.2.2.x.x.x.x.x.x.y.y.y$

2).

$64x^{3}y = 2.2.2.2.2.2.x.x.x.y$

$44xy = 11.2.2.x.y$

$36x^{2}y^{2} = 3.3.2.2.x.x.y.y$

G.C.F = $2.2.x.y = 4xy$