JUMP TO TOPIC
Function operations are the arithmetic operations that are used to solve a function. The arithmetic operations applied to a function are addition, subtraction, multiplication, and division.
In this article, we will learn about functions and how we can apply different operations to functions.
What Are Function Operations?
Function operations are the arithmetic rules we can apply to two or more functions. Functions can be added, subtracted, multiplied, or divided against each other, and we can divide function operations into four types.
- Addition of the functions
- Subtractions of the functions
- Multiplication of the functions
- Division of the functions
Addition of the Functions
When two or more functions are added together, it is called the addition of functions or functions addition rule. For example, we have two functions $f(x)$ and $g(x)$ and if we add them together then we will get $(f+g)(x) = f(x) + g(x)$. Suppose $f(x) = 2x$ and $g(x) = 3x+1$, then $(f+g)(x) = f(x) + g(x) = 2x + 3x +1 = 5x +1$.
Example 1: If $f(x) = 5x -3$ and $g(x) = 6x +2$, find out the function $(f+g) (x)$ at $x = 3$,$4$ and $5$.
Solution:
$f(x) = 5x – 3$
$g(x) = 6x + 2$
$(f+ g) (x) = 5x -3 +6x +2$
$(f+ g) (x) = 11x – 1$
At $x = 3$
$(f+ g) (3) = 11 (3) – 1 = 33 – 1 = 32$
At $x = 4$
$(f+ g) (4) = 11 (4) – 1 = 44 – 1 = 43$
At $x = 5$
$(f+ g) (5) = 11 (5) – 1 = 55 – 1 = 54$
Example 2: If $f(x) = 2x^{2} + 2$ and $g(x) = 6x – 1$, find out the function $(f+g) (x)$ at $x = 2$ and draw the graph of the addition function.
Solution:
$f(x) = 2x^{2} + 1$
$g(x) = 6x – 2$
$(f+ g) (x) = 2x^{2} + 1 + 6x -2$ = 2x^{2} + 6x – 1
$(f+ g) (x) = 2x^{2} + 6x – 1$
At $x = 2$
$(f+ g) (2) = 2 (2)^{2} + 6 (2) – 1 = 8 + 12 – 1 = 194$
The graph of the three functions is shown below.
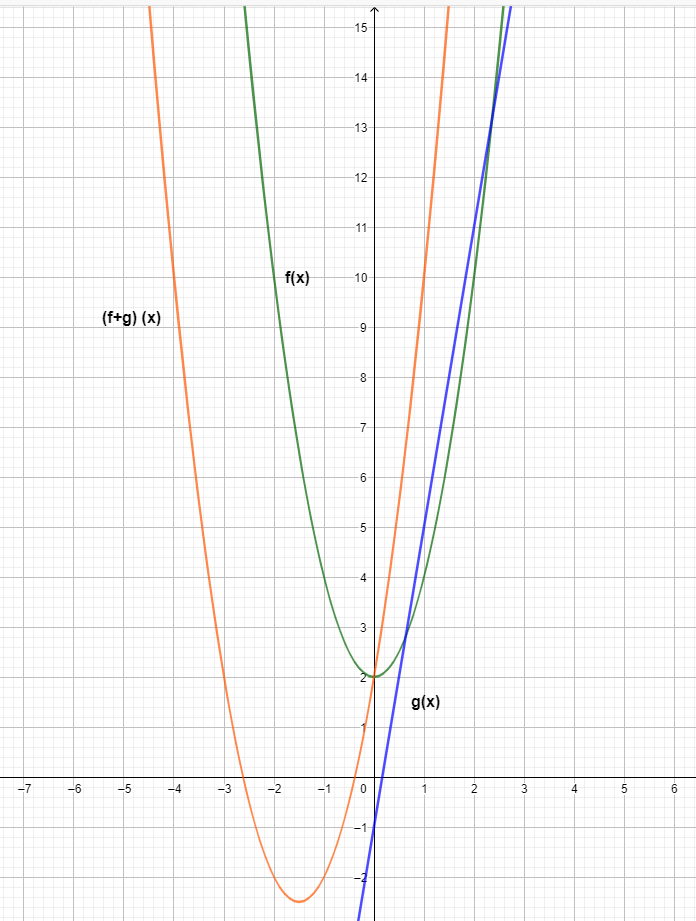
From the graph, we can see that the y-coordinate value of the addition function $(f+g) (x)$ is the result of the addition of individual functions $f(x)$ and $g(x)$.
Subtraction of the Functions
When two or more functions are subtracted, it is called the subtraction of functions or functions subtraction rule. For example, we have two functions $f(x)$ and $g(x)$ and if we subtract them, then we will get $(f – g)(x) = f(x) – g(x)$. Suppose $f(x) = 5x$ and $g(x) = 3x -1$ then $(f-g)(x) = f(x) – g(x) = 5x – (3x-1) = 5x – 3x + 1 = 2x + 1 $.
Example 3: If $f(x) = 7x -3$ and $g(x) = -4x +11$, find out the function $(f-g) (x)$ at $x = 1$,$2$ and $3$.
Solution:
$f(x) = 7x – 3$
$g(x) = -4x + 11$
$(f – g) (x) = 7x -3 – (-4x +11)$
$(f – g) (x) = 7x – 3 + 4x -11 = 11x – 14$
At $x = 1$
$(f – g) (3) = 11 (1) – 14 = 11 – 14 = -3$
At $x = 2$
$(f – g) (4) = 11 (2) – 14 = 22 – 14 = 6$
At $x = 3$
$(f – g) (5) = 11 (3) – 14 = 33 – 14 = 9$
Example 4: If $f(x) = 4x^{2} – 2$ and $g(x) = 5x +3$, find out the function $(f – g) (x)$ at $x = 3$ and draw the graph of the function $(f-g)(x)$.
Solution:
$f(x) = 4x^{2} – 2$
$g(x) = 5x + 3$
$(f – g) (x) = 4x^{2} – 2 – (5x +3) = 4x^{2} – 2 – 5x – 3 = 4x^{2} -5x -5$
$(f – g) (x) = 4x^{2} -5x -5$
At $x = 3$
$(f – g) (3) = 4 (3)^{2} – 5 (3) – 5 = 36 – 15 – 5 = 16$
The graph of the three functions is shown below.
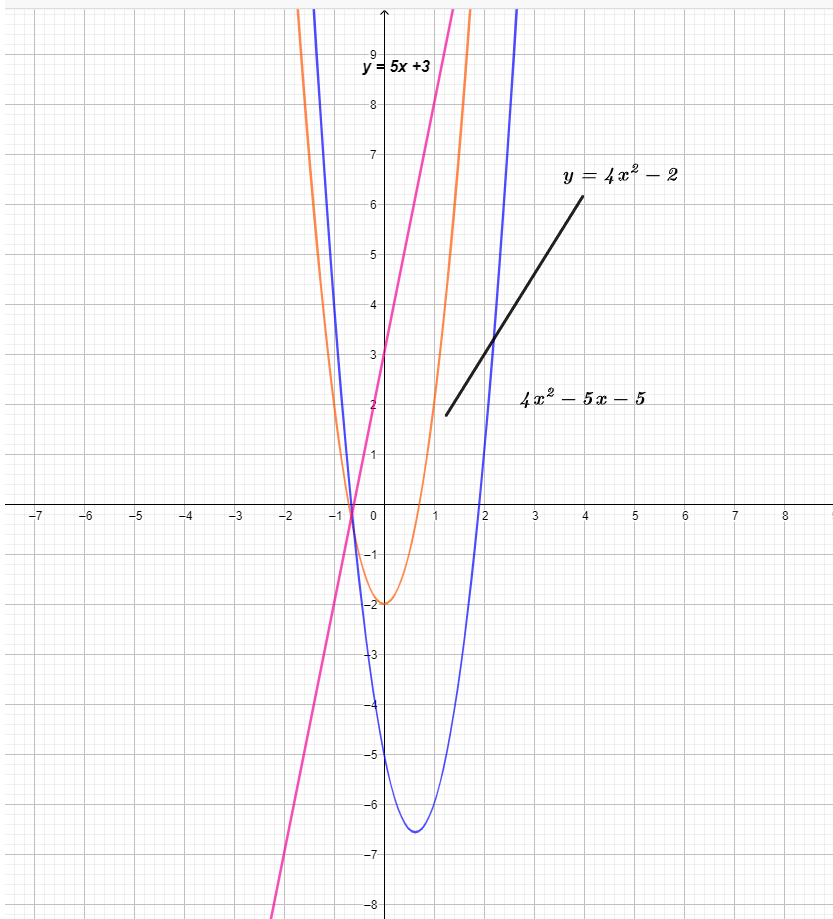
From the graph, we can see that the y-coordinate value of the function $(f – g) (x)$ is the result of the subtraction of the function $g(x)$ from the function $f(x)$.
Multiplication of the Functions
Let us consider an example of function operations multiplication: we have two functions f(x) and g(x) and if we multiply them together, then we will get $(f \times g) (x)$ = $f(x) \times g(x)$. Suppose $f(x) = 6x$ and $g(x) = 4x$ then $(f \times g)(x) = f(x) \times g(x) = 6x \times 4x = 24x^{2}$.
Example 5: If $f(x) = 3x -1$ and $g(x) = 4x$, find out the function $(f \times g) (x)$ at $x = 2$ and $3$.
Solution:
$f(x) = 3x – 1$
$g(x) = 4x$
$(f \times g) (x) = (3x-1) (4x)$
$(f \times g) (x) = 12x^{2} – 4x$
At $x = 2$
$(f \times g) (2) = 12 (2)^{2} – 4(2) = 48 – 8 = 40$
At $x = 3$
$(f \times g) (3) = 12 (3)^{2} – 4(3) = 108 – 12 = 96$
Example 6: If $f(x) = 2x +1$ and $g(x) = 2x – 1$. Determine the function $(f \times g) (x)$ and how the function $(f \times g) (x)$ is different from $f(x)$ and $g(x)$.
Solution:
$f(x) = 2x + 1$
$g(x) = 2x – 1$
$(f \times g) (x) = (2x + 1) (2x-1) = (2x)^{2} – (1)^{2}$
$(f \times g) (x) = 4x^{2} -1$
The graph of the three functions is shown below.
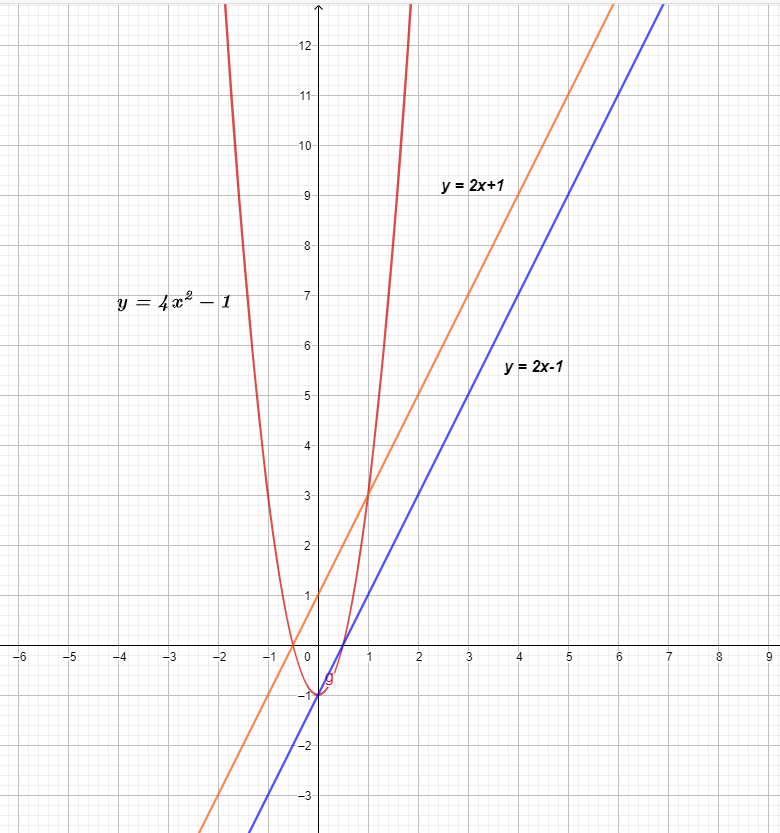
The graph of the $f(x)$ and $g(x)$ shows a straight line, which means they are linear functions, but when multiplied, they result in a non-linear quadratic function $( f \times g) (x) = 4x^{2}- 1$.
Division of the Functions
To understand the function operations division, suppose we have two functions $f(x)$ and $g(x)$ and if we divide them, then we will get $(\dfrac{f}{g})(x) = \dfrac{f(x)}{g(x)}$. Suppose $f(x) = 6x$ and $g(x) = 3x$ then $(\dfrac{f}{g})(x) = \dfrac{f(x)}{g(x)} = \dfrac{6x}{3x} = 2$.
Example 7: If $f(x) = 21 x^{2}$ and $g(x) = 3x$, find out the function $(\dfrac{f}{g}) (x)$ at $x = 5$.
Solution:
$f(x) = 21 x^{2}$
$g(x) = 3x$
$(\dfrac{f}{g}) (x) = \dfrac{21 x^{2}}{3x}$
$(\dfrac{f}{g}) (x) = 7x$
At $x = 5$
$(\dfrac{f}{g}) (5) = 7 (5) =35$
Example 8: If $f(x) = 4x^{2} + 8x + 16$ and $g(x) = 4x$, find out the function $(\dfrac{f}{g}) (x)$ at $x =2$.
Solution:
$f(x) = 4x^{2} + 8x +16$
$g(x) = 4x$
$(\dfrac{f}{g}) (x) = \dfrac{4x^{2} + 8x +16}{4x} = 4 (\dfrac{x^{2} + 2x +4}{4x})$
$(\dfrac{f}{g}) (x) = \dfrac{x^{2} + 2x +4}{x}$
At $x = 2$
$(\dfrac{f}{g}) (2) = \dfrac{(2)^{2} + 2(2) + 4}{2} = \dfrac{12}{2} = 6$
The examples we have discussed so far will surely help you in test preparation related to function operations and composition.
What Is a Function?
A function is an expression that is used to show a relation between two or more variables. If a function has two variables, then one variable will be the input variable while the other will be the output variable.
The function is generally written as $f(x)$. For example, if we are given an equation $f(x) = y = 3x + 5$, we will say that the variable “$x$” is the input variable and the variable “$y$” is the output variable.
Function and Variables
We can say that a function represents a relationship between a dependent and independent variable in the form of an equation. In the example $f(x) = y = 3x + 5$, “$x$” will be the independent variable and “$y$” will be the dependent variable. The value of “$y$” will depend upon the value of “$x$”, which is why it is called the dependent variable. All the possible values of “$x$” will be called the function’s domain, and the corresponding output values of “y” will be called the range of the function.
For example, if we are given a function $f(x) = y = 6x$ and we want to calculate the value of “$y$” at x = $1$,$2$ and $3$, then:
At $x = 1$
$y = 6 (1) = 6$
At $x = 2$
$y = 6 (2) = 12$
At $x = 3$
$y = 6 (3) = 18$
Here, the domain of the function will be $1$,$2$,$3$, and the range of the function will be $6$,$12$, and $18$. In this case, we were only dealing with one function. What if we have two functions, say $f(x)$ and $g(x)$, and we have to add or subtract these functions? This is where operations of the functions play their part.
Practice Questions
- If $f(x) = 3x^{3} – 9x$ and $g(x) = 3x$, find out the function $(\dfrac{f}{g}) (x)$ at $x = 4$.
- If $f(x) = 4x + 2$ and $g(x) = 2x + 5$, find out the function $(f \times g) (x)$ at $x = 2$.
- If $f(x) = -3x -1$ and $g(x) = 5x – 2$, find out the function $(f + g) (x)$ at $x = 7$.
Answer Keys:
1).
$f(x) = 3x^{3} – 9x$
$g(x) = 3x$
$(\dfrac{f}{g}) (x) = \dfrac{3x^{3} – 9x}{3x} = 3x (\dfrac{x^{2} + 3}{3x})$
$(\dfrac{f}{g}) (x) = x^{2} + 3$
At $x = 4$
$(\dfrac{f}{g}) (4) = 4^{2} + 3 = 19$
2).
$f(x) = 4x +2$
$g(x) = 2x + 5$
$(f \times g) (x) = (4x + 2) (2x +5)$
$(f \times g) (x) = 8x^{2} + 4x + 20x + 10 = 8x^{2} + 24x +10$
At $x = 2$
$(f \times g) (2) = 8(2)^{2} + 24 (2) +10 = 32 + 48 +10 = 90$
3).
$f(x) = -3x – 1$
$g(x) = 5x – 2$
$(f + g) (x) = -3x -1 +5x – 2$
$(f + g) (x) = 2x – 3$
At $x = 7$
$(f + g) (7) = 2(7) – 3 = 14 – 3 = 11$