JUMP TO TOPIC
 If we expand a number as a summation of individual digits multiplied by powers of $10$, then we call it the expanded form exponents.
If we expand a number as a summation of individual digits multiplied by powers of $10$, then we call it the expanded form exponents.
In this topic, we will learn how to expand any given number using exponents. We will cover integers as well as decimal numbers using many numerical examples.
What Is Expanded Form Exponents?
When an integer or a decimal is expanded using the exponents, then it is called expansion with exponents or expanded form exponents. In the exponential form, there is a base number and the power of the base is known as its exponent.
Expanded Form
The expanded form of any number is the expansion of the said number as individual digits. In the expanded form we add all the values of each individual and it will give us the original number.
In short, we divide the number into ones, tens, hundreds etc and then add all those digits to get the original number. If we are given a number $121$, then we can divide this number into three parts: units, tens and hundreds as: $121 = 100\times 1 + 2 \times 10 + 1 \times 1 = 100 + 20 + 1$ and this is called the expansion of a number.
So in short, we can say that in the expanded form the digits of the number are associated with an expression which has the same digits but each digit is then multiplied with a base of $10$ with an exponent in such a manner that if we add them all up we get the original number.
Writing a Number in Expanded Form
The method of writing a number in expanded form is very easy. Suppose we have a number “$a$” and we can divide into “$n$” digits, we can write it as $a = x_{n-1} \cdots x_{3} x_{2} x_{1}x_{0}$. Here, $x_{0}$ is the ones or units digit while $x_{1}$ the tens digits, $x_{2}$ the hundreds digit, and so on.
Let $a=321$, then $n=3$ and $x_{2}=3$, $x_{1} = 2$, and $x_{0}=1$.
Now, we want to expand $a$ as a summation of $n$ numbers, i.e., $a = c_{n-1} + c_{n-2} + \cdots + c_{0}$. In such a case, $c_{0}$ will be equal to $x_{0}$, $c_{1}$ will be equal to $x_{1}$ but with one extra zero at the end. Similarly, $c_{2}$ will be equal to $x_{2}$ but with two zeros appended at the end. For example, for $a=321$, we can write:
$a = 300 + 20 + 1$. Note that in this case, $c_{0}=1=x_{1}$, $c_{1}=20=x_{1}0$ and $c_{2}=300=x_{3}00$.
This expansion method which we discussed is suitable for integers, but what if the number which we are given for expansion is not an integer but a decimal, then what should be done? Well, this is where expansion with exponents comes in handy. Let us discuss what is meant by expansion with exponents and how we can use it to expand decimal numbers.
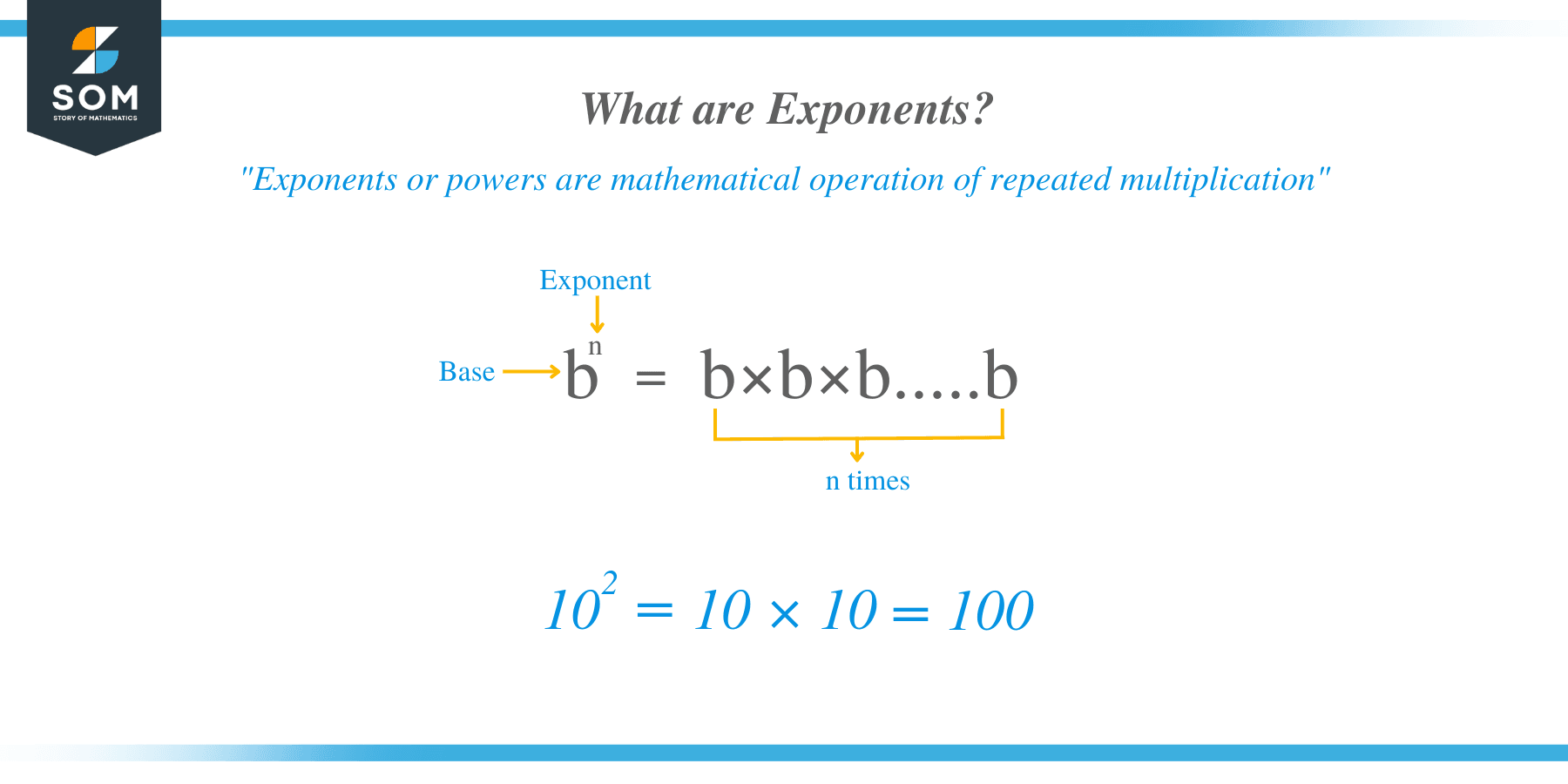
Expansion Statement
Expanded Form Exponents is just like the normal expansion which we have discussed in the previous section but we do the expansion using the exponents. If you remember the expansion statement:
$a = x_{n-1} …… x_{3} x_{2} x_{1} x_{0} = c_{n-1}+ …… + c_{3} + c_{2}+ c_{1} + c_{0}$
Earlier, we added zeros at end of each “$c$” depending upon the base value. Instead, we can remove the extra zeros and multiply the digit with “$10^{k}$”, where “$k$” is the power of the exponent. For example, if we are given a digit $x_{2}$ then we can write $c_{2} = x_{2} \times 10^{2}$. The general expression can be written as $c_{n} = x_{n} \times 10^{n}$.
For example, we take the same previous number $321$ and now let us expand it using the exponent method. The digit “$3$” is the hundred digit while the digit “$2$” is the tens and “1” is the unit digit. $x_{2} = 3$, $x_{1} = 2$ and $x_{0} = 1 $ and we can write the term as $c_{2} = 3 \times 10^{2}$, $c_{1} = 2 \times 10^{1}$ and $c_{0} = 1 \times 10^{0}$ so if we add all the “c” terms we get $321 = 3 \times 10^{2} + 2 \times 10^{1} + 1 \times 10^{0} = 3 \times 100 + 2 \times 10 + 1 \times 1 = 300 + 20 + 1$.
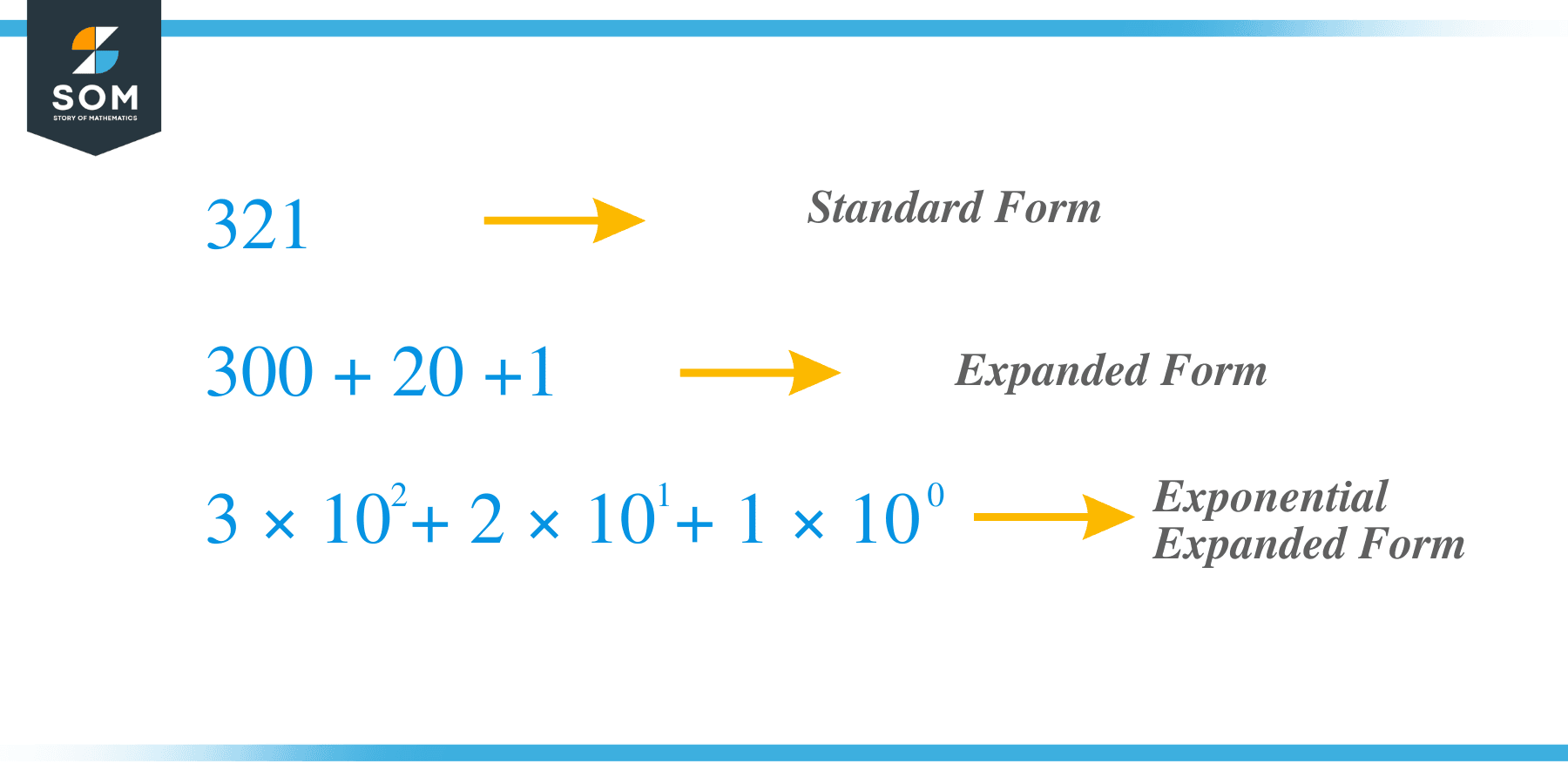
Let us study some of the examples related to the expansion of numbers using the exponent method.
Example 1: Expand the number $6565$ using the exponent method.
Solution:
The number $6565$ can be separated into digits $6$,$5$,$6$, and $5$.
Let $x = 6565$, then $x_{3} = 6, x_{2} = 5, x_{1} = 6, x_{0} = 5$
$6565 = 6 \times 10^{3} + 5 \times 10^{2} + 6 \times 10^{1} + 5 \times 10^{0}$
$6565 = 6 \times 1000 + 5 \times 100 + 6 \times 10 + 5 \times 1$
$6565 = 6000 + 500 + 60 + 5$
Example 2: Expand the number $7012$ using the exponent method.
Solution:
The number $7012$ can be separated into digits $6$,$5$,$6$, and $5$.
Let $x = 7012$, then $x_{3} = 7, x_{2} = 0, x_{1} = 1, x_{0} = 2$
$7012 = 7 \times 10^{3} + 0 \times 10^{2} + 1 \times 10^{1} + 2 \times 10^{0}$
$7012 = 7 \times 1000 + 0 \times 100 + 1 \times 10 + 2 \times 1$
$7012 = 7000 + 0 + 10 + 2$
Example 3: Expand the number $30492$ using the exponent method.
Solution:
The number $30492$ can be separated into digits $6$,$5$,$6$, and $5$.
Let $x = 30492$, then $x_{4} = 3$,$ x_{3} = 0$, $x_{2} = 4$, $x_{1} = 9$, $x_{0} = 2$
$30492 = 3 \times 10^{4} + 0 \times 10^{3} + 4 \times 10^{2} + 9 \times 10^{1} + 2 \times 10^{0}$
$30492 = 3 \times 10000 + 0 \times 1000 + 4 \times 100 + 9 \times 10 + 2 \times 1$
$30492 = 30000 + 0 + 400 + 90 + 2$
Expansion of Decimal Numbers
The decimal numbers can easily be expanded using the expansion with exponents. In the case of numbers, the digit on the far right is termed as a unit digit and it is multiplied by “$10^{0}$” but in the case of decimal numbers, there are digits after the decimal point. For example, the number 145.65 is considered a decimal number. So how do you expand the numbers after the decimal point?
It can easily be done by separating the digits before and after the decimal point. The digits prior to decimal points are $1$,$4$, and $5$, and we will expand them with the same method we have used so far, i.e., $x_{2} = 1$, $ x_{1} = 4$ and $x_{0} = 5$. We will multiply each digit with $10^{k}$, where $k$ depends upon the base value of “$x$”.
In the case of digits prior to the decimal point, we start from the right and multiply each digit with “10” while increasing the power of “$10$” by “$1$”; as a general expression, we can write it as:
$a = x_{n-1} \times 10^{n-1} + x_{n-2} \times 10^{n-2} + \cdots + x_{0} \times 10^{0}$
In the case of digits after the decimal point, we start from the left and multiply each digit with “10” while decreasing the power of “$10$” by “$1$”. As a general expression, we can write it as:
$a = b_{1} \times 10^{-1} + b_{2} \times 10^{-2} + \cdots + b_{n} \times 10^{-n}$
For the digits after the decimal point, we start decreasing the exponent of base “$10$” from left to right. Continuing the above example of number 145.65, the number after the decimal point can be written as $0.65 = 6 \times 10^{-1} + 5 \times 10^{-2} = 0.6 + 0.05$. So if we want to expand the decimal number $145.65$ using exponents, then it can be done as:
$145.65 = 1 \times 10^{2} + 4 \times 10^{1} + 5 \times 10^{0} + 6 \times 10^{-1} + 5 \times 10^{2} = 100 + 40 + 5 + 0.6 + 0.05$
As you can see, if we start from the right-most digit in this example which is 1, it was multiplied by $10^{2}$ as it was at a hundred place and as we moved to the left, we decreased the power of base “$10$” by $1$.
Let us discuss an example of an expanded exponential form of a decimal number.
Example 4: Expand the number $920.12$ using the exponent method.
Solution:
The number $920.12$ can be separated into digits 9,2,0, 1, and 2.
Let $x = 920.12$, then $c_{2} = 9$, $c_{1} = 2$, $c_{0} = 0$, $b_{1} = 1$, $b_{2} = 2$
$920.12 = 9 \times 10^{2} + 2 \times 10^{1} + 0 \times 10^{0} + 1 \times 10^{-1} + 2 \times 10^{-2}$
$920.12 = 9 \times 100 + 2 \times 10 + 0 \times 1 + \dfrac{1}{10} + \dfrac{2}{100}$
$920.12 = 900 + 20 + 0 + 0.1 + 0.02$
This is how decimals in the expanded form are presented or written.
Practice Questions
- Expand the number $-121.40$ using the exponent method.
- Write $224,090$ in expanded form using exponents.
Answer Key:
1).
The number is negative and there are two methods to solve this. You can either follow the first method which we have discussed and just simply multiply the final answer with “$-1$”, or take every digit as negative to expand the number.
$-121.40$ can be separated in to digits $-1$,$-2$,$-1$,$- 4$, and $0$.
Let $x = -121.40$, then $c_{2} = -1$, $c_{1} = -2$, $c_{0} = -1$, $b_{1} = -4$, b_{2} = 0$
$-121.40 = -1 \times 10^{2} – 2 \times 10^{1} – 1\times 10^{0} – 4 \times 10^{-1} – 0 \times 10^{-2}$
$-121.40 = -1 \times 100 – 2 \times 10 – 1 \times 1 – \dfrac{4}{10} – \dfrac{0}{100}$
$-121.40 = -100 – 20 – 1 – 0.4 – 0$
2).
The number $224,090$ can be separated into digits $2$,$2$,$4$, $0$,$9$, and $5$.
Let $x = 224,090$, then $x_{5} = 2$, $x_{4} = 2$,$ x_{3} = 4$,$ x_{2} = 0$, $x_{1} = 9 $, $x_{0} = 0$
$224,090 = 2 \times 10^{5} + 2 \times 10^{4} + 4 \times 10^{3} + 0 \times 10^{2} + 9 \times 10^{1} + 0 \times 10^{0}$
$224,090 = 2 \times 100000 + 2 \times 10000 + 4 \times 1000 + 0 \times 100 + 9 \times 1 + 0 \times 1$
$224,090 = 200000 + 20000 + 4000 + 0 + 90 + 0$
