How Many Sides Does a Circle Have – Definition and Examples

In the simplest terms, a circle is a two-dimensional shape that is perfectly round and consists of all points in a plane that are equidistant from a fixed center point. This distance from the center to any point on the circle is known as the radius.

Basic Properties of a Circle

Circumference

The circumference of a circle is the distance around it, or the circle’s perimeter. The circumference (C) can be calculated using the formula C = 2πr, where r is the radius of the circle.

Diameter

The diameter of a circle is the longest distance across the circle. It is twice the length of the radius, so the diameter (d) is d = 2r.

Radius

As mentioned above, the radius is the distance from the center of the circle to any point on its edge.

Area

The area (A) of a circle is the number of square units it encloses, which can be calculated with the formula A = πr², where r is the radius of the circle.

Pi (π)

Pi is a mathematical constant approximately equal to 3.14159, representing the ratio of the circumference of a circle to its diameter. It is an irrational number, which means its decimal representation never ends or repeats.

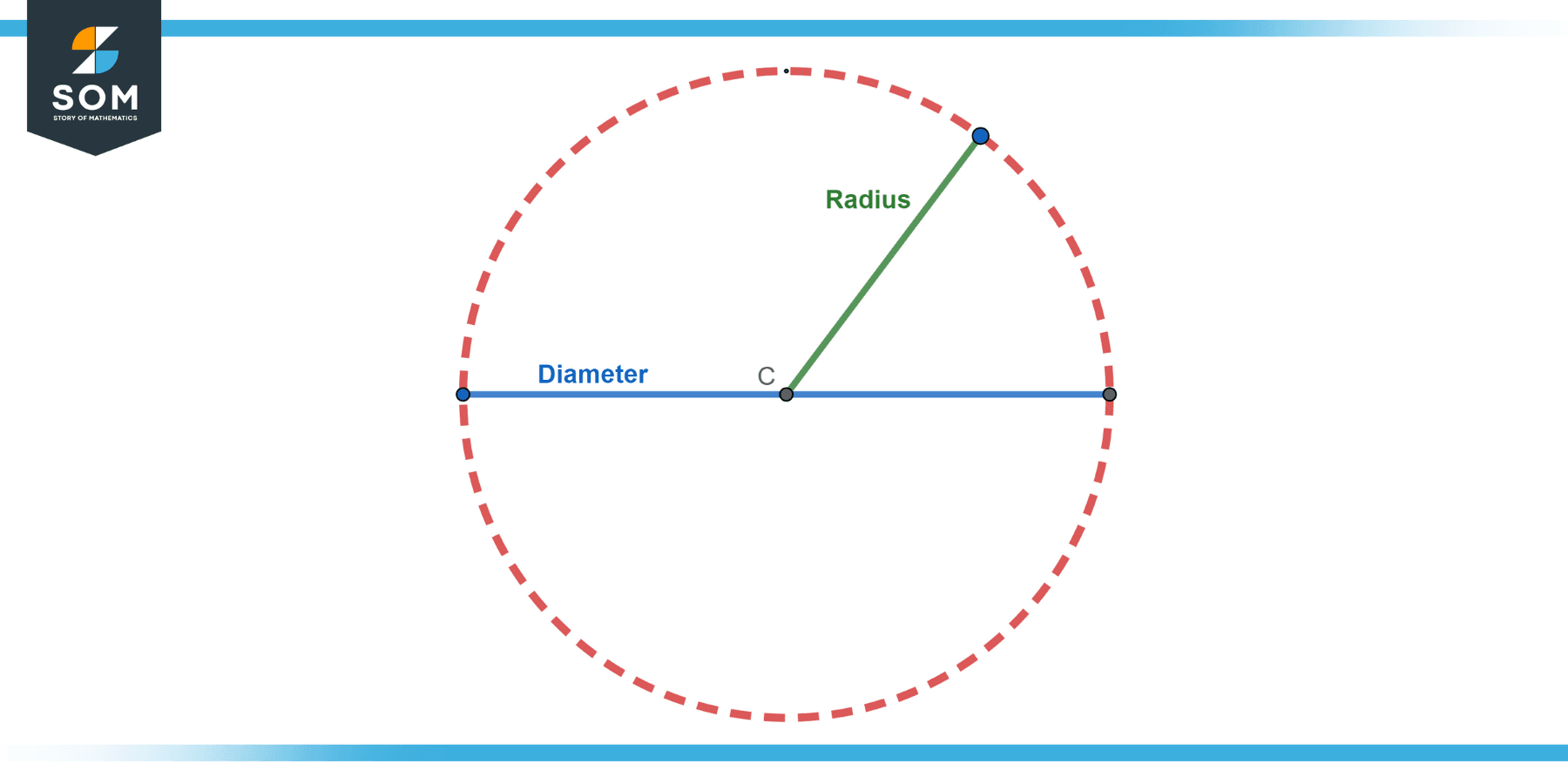
Figure-2.

Concept of Sides of a Circle

In traditional geometric terms, a circle is not said to have sides because it does not consist of straight-line segments. However, from different perspectives, a circle can be interpreted as having one side (considering the circumference as a continuous curve), two sides (distinguishing between the interior and exterior), or an infinite number of sides (considering it as the limit of a regular polygon with an increasing number of sides).

Chords, Secants, and Tangents

A chord of a circle is a straight line segment whose endpoints lie on the circle. The diameter is the longest possible chord of a circle. A secant line is a line that intersects a circle at two points, while a tangent line is a line that “touches” the circle at exactly one point.

Properties

Exploring the properties of a circle through the lens of how many sides it has is an interesting endeavor. As previously mentioned, we have three main perspectives on this matter: a circle having no sides, one side, or infinite sides. Let’s delve into the properties associated with each.

No Sides

This perspective is grounded in the classical definition of a circle, and it leads us to the basic properties of a circle:

Circumference

The distance around the circle is given by the formula 2πr, where r is the radius.

Area

The space enclosed by the circle is given by the formula πr².

Center

Every point on the circle is equidistant from the center.

Diameter

A line segment passing through the center and touching the circle at both ends is the diameter. It’s twice the radius.

No vertices

In this perspective, a circle doesn’t have any vertices or corners.

One or Two Sides

From a more abstract mathematical perspective, a circle could be thought of as having one or two sides:

One Side

If we consider the “side” to be the curved boundary of the circle (the circumference), then it has one continuous, unbroken side.

Two Sides

Some might consider a circle to have two sides: the outside (exterior) and the inside (interior). The interior is all the points within the circle, and the exterior is everything outside of it.

Infinite Sides

In certain mathematical contexts, a circle could be considered a polygon with an infinite number of sides:

• As the number of sides in a regular polygon increases, the shape becomes more and more like a circle. If you consider a polygon with an infinite number of infinitesimally small sides, it would essentially be a circle.
• From this viewpoint, each “side” would be a tangent line to the circle at a specific point.
• Each “vertex” would be a point on the circle where two adjacent tangents meet. Since the sides are infinitesimally small, there would be an infinite number of vertices.

Remember, these are interpretations of how many sides a circle has, each revealing unique aspects of the nature of a circle. However, in a standard mathematical context, the accepted view is that a circle does not have sides in the same way a polygon does.

Ralevent Formulas 

While the question “How many sides does a circle have?” isn’t typically associated with any specific mathematical formulas, it does implicitly lead us toward several key mathematical concepts and associated equations.

No Sides (Classical Perspective)

Here, we would deal with the basic properties of a circle, which have associated formulas:

Circumference

The total distance around the circle is given by the formula C = 2πr, where r is the radius of the circle.

Area

The total space enclosed by the circle, also known as the area, is given by the formula A = πr², where r is the radius of the circle.

Diameter

The longest distance from one end of the circle to the other, passing through the center, is called the diameter and is given by the formula d = 2r, where r is the radius of the circle.

One Side (abstract perspective)

Considering the circle’s perimeter as a single, continuous side, the length of this side is equivalent to the circle’s circumference, which, as mentioned above, is given by C = 2πr.

Two Sides (abstract perspective)

Here, we may think of the interior and exterior of the circle as two distinct “sides.” While it’s a more conceptual interpretation rather than a direct application of a formula, it does lead to the exploration of concepts like interior and exterior angles, typically in the context of polygons.

Infinite Sides (limits perspective)

When we consider a circle as the limit of an n-sided regular polygon as n approaches infinity, we can use the formula for the perimeter of a regular n-sided polygon to derive the circle’s circumference.

• For a regular n-sided polygon with side length s, the perimeter P = ns.
• If the polygon is inscribed in a circle of radius r, as n approaches infinity, the length of each side s approaches zero, and the perimeter P = ns approaches the circumference of the circle, C = 2πr.

These formulas reflect different ways to interpret the question “How many sides does a circle have?”, providing a variety of mathematical contexts to understand and analyze the unique and intriguing properties of a circle.

Exercise 

Example 1

No Sides – Circumference

Find the circumference of a circle with a radius of 5 units.

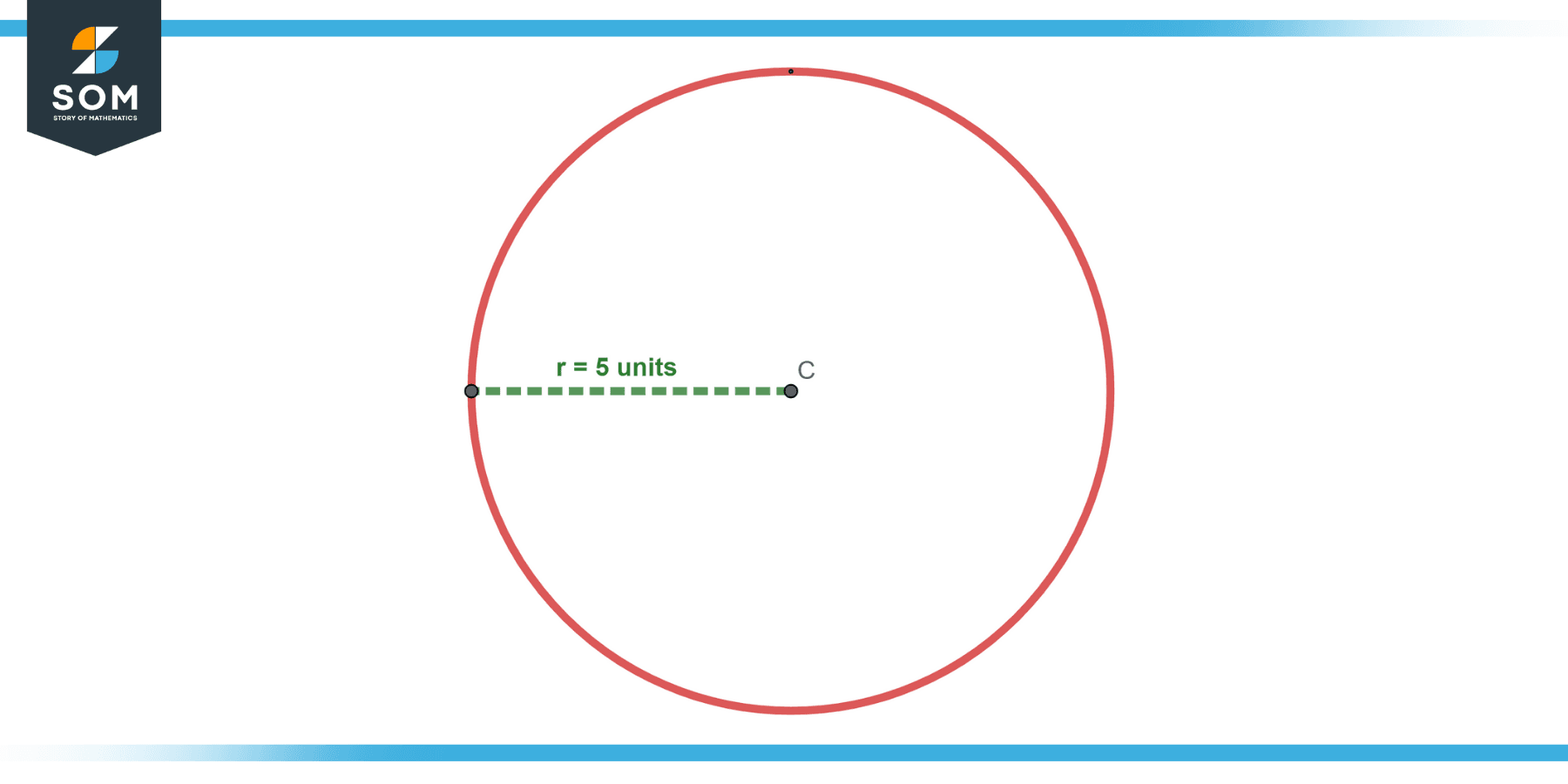
Figure-3.

Solution

Use the formula for circumference, C = 2πr. Substituting r = 5, we get:

C = 2π * 5

C = 10π units

Example 2

No Sides – Area

Calculate the area of a circle with a radius of 7 units.

Figure-4.

Solution

Use the formula for the area, A = πr². Substituting r = 7, we get:

A = π * (7)²

A = 49 * π square units

Example 3

One Side – Circumference

If a circle’s circumference (considered as one continuous side) is 31.4 units, find its radius.

Solution

Rearrange the formula for circumference to find the radius:

r = C / 2π

Substituting C = 31.4, we get:

r = 31.4 / 2π

r = 5 units

Example 4

One Side – Diameter

If a circle’s circumference (considered as one continuous side) is 44 units, find its diameter.

Solution

Use the formula for circumference:

C = π * d

Rearrange to find the diameter:

d = C / π

Substituting C = 44, we get:

d = 44 / π

d ≈ 14 units

Example 5

Two Sides – Interior and Exterior

Consider a circle of radius r. If a regular n-sided polygon is inscribed in the circle, show that the sum of the interior angles of the polygon is (n-2) * 180 degrees.

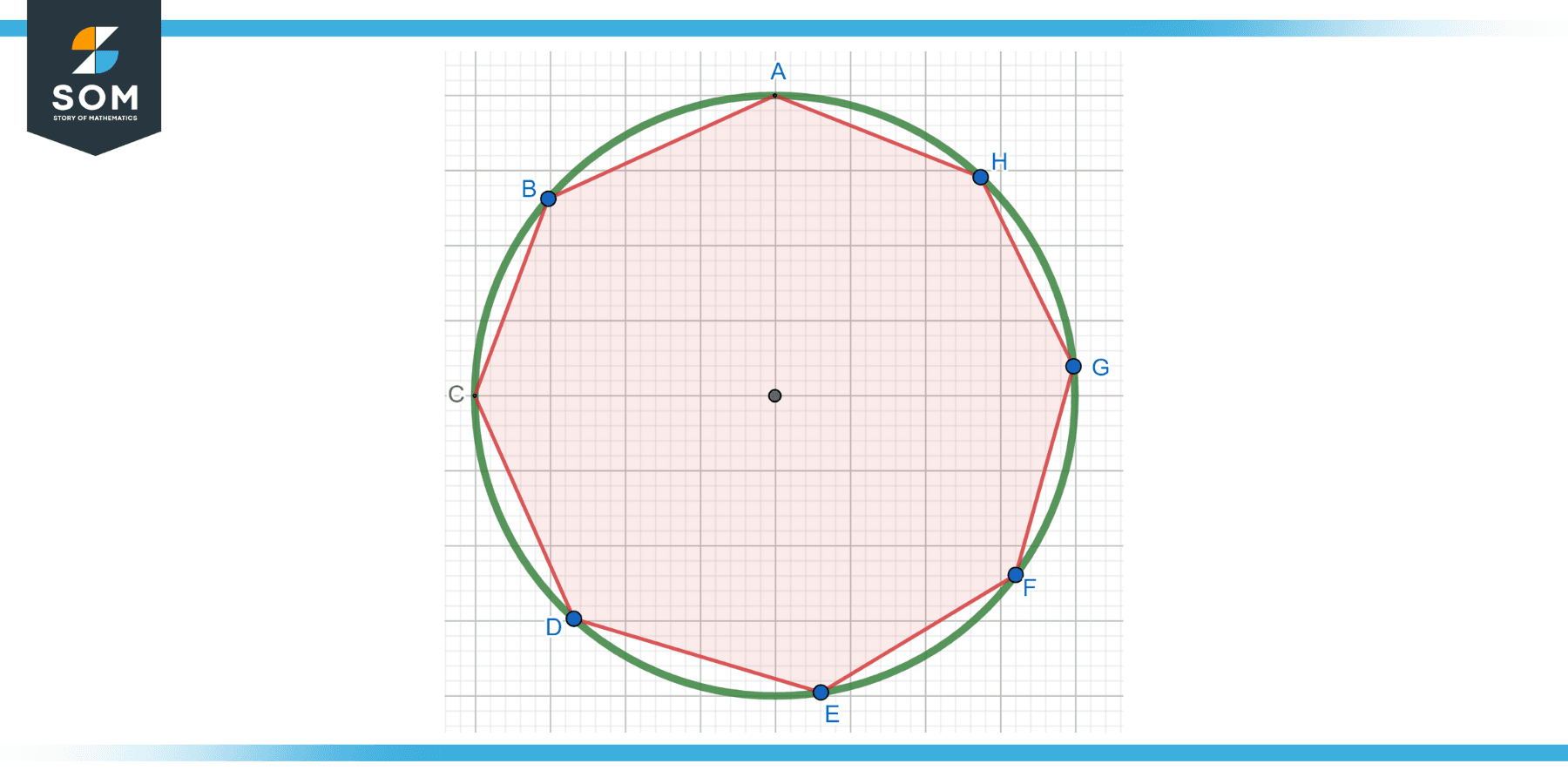
Figure-5.

Solution

This is a property of polygons. It’s not a direct measure of the circle’s sides but demonstrates the difference between a circle (with two conceptual sides, the interior, and the exterior) and a polygon with distinct sides.

Example 6

Infinite Sides – Circumference

A circle is a limit of an inscribed regular polygon with n sides, each of length s. As n approaches infinity, show that the circle’s circumference is the limit of the polygon’s perimeter.

Solution

The perimeter of the polygon is P = ns. As n approaches infinity, s approaches 0, but ns approaches 2πr, the circumference of the circle.

Example 7

Infinite Sides – Area

A circle is a limit of an inscribed regular polygon with n sides, each of length s. As n approaches infinity, show that the circle’s area is the limit of the polygon’s area.

Solution

The area of the polygon can be calculated using various formulas involving n, s, and r. As n approaches infinity, this area approaches πr², the area of the circle.

Example 8

Infinite Sides – Calculus

Use integral calculus to calculate the length of a semicircular arc (considered as an infinite number of infinitesimal straight-line segments) with radius r.

Solution

The length of a semicircular arc is half the circle’s circumference, which is given by:

l = (1/2) * 2πr

l = π * r

Example 9

One Side – Arc Length

A circle with a radius of 10 units has been divided into an arc of 60 degrees. Calculate the length of this arc.

Solution

The length of the arc (which can be considered as a “side” of a portion of the circle) is given by the formula:

L = 2πr * (θ/360)

where θ is the angle of the arc in degrees. So:

L = 2π * 10 * (60/360)

L = 10π/3

L ≈ 10.47 units

Example 10

Two Sides – Area Difference

Given a circle of radius 5 units and a square inscribed in it, find the difference between the area of the circle (considered one “side”) and the square.

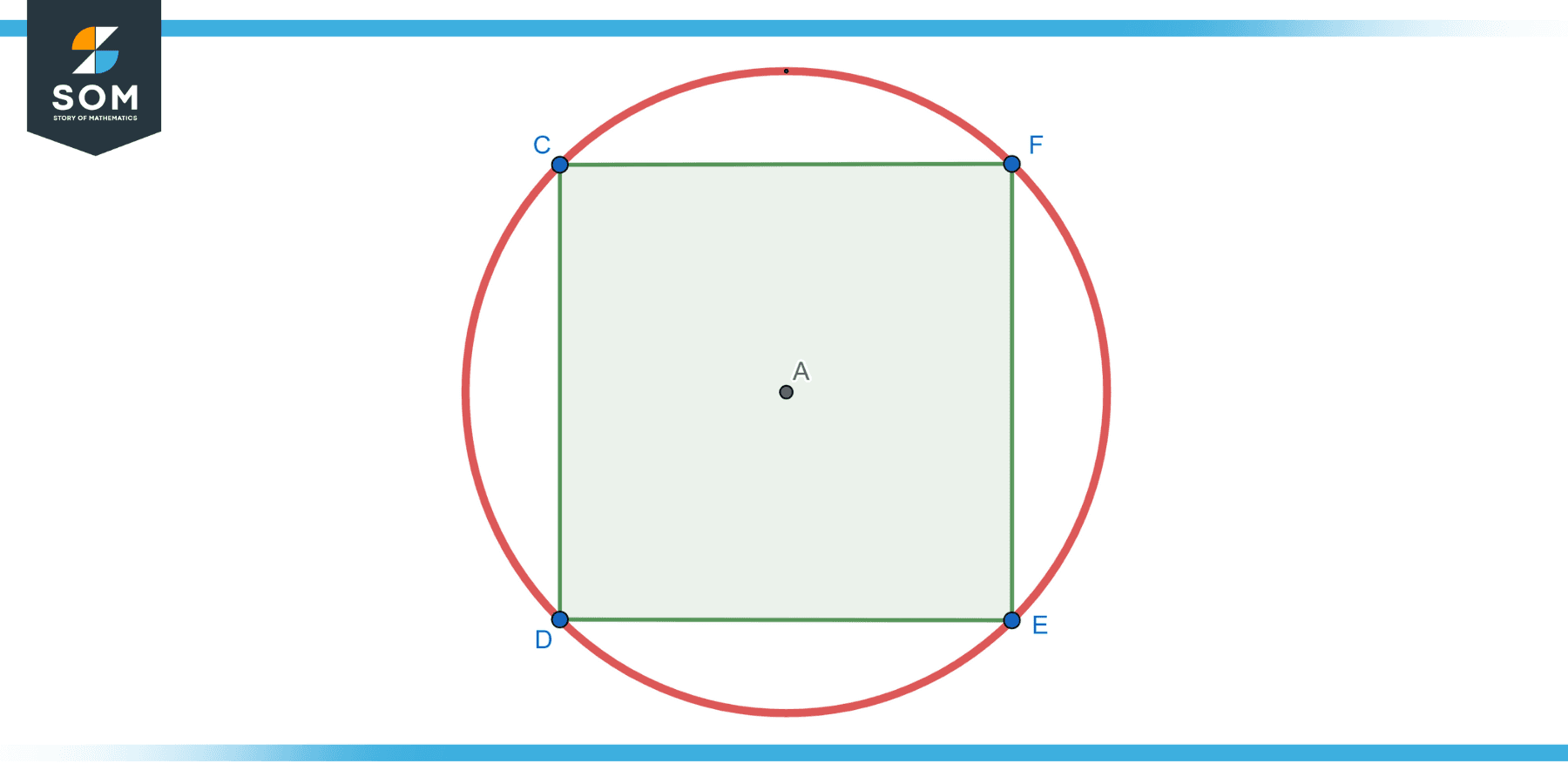
Figure-6.

Solution

The diameter of the circle is the same as the diagonal of the square. Therefore, the side of the square (s) is √2 * r, and its area is s². The area of the circle is πr². The difference in areas is given as follows:

d = πr² – s²

d = π(5)² – (√2 * 5)²

d = 25π – 50

d ≈ 28.54 square units

Example 11

Infinite Sides – Perimeter Limit

Consider a regular hexagon inscribed in a circle of radius r. Show that as the number of sides of the regular polygon increases (tending to infinity, implying a circle), the perimeter of the polygon approaches the circumference of the circle.

Solution

The side of a regular hexagon inscribed in a circle of radius r is also of length r. Therefore, the perimeter of the hexagon is 6 * r.

As the number of sides increases, each side length remains r (since each side is a radius of the circle), but the number of sides approaches infinity. Therefore, the perimeter approaches infinity * r = 2πr, the circumference of the circle.

Example 12

Infinite Sides – Area Limit

Consider a regular octagon inscribed in a circle of radius r. Show that as the number of sides of the regular polygon increases (tending to infinity, implying a circle), the area of the polygon approaches the area of the circle.

Solution

The area A of a regular polygon with n sides, each of length s, inscribed in a circle of radius r is given by:

A = 0.5 * n * s² * cot(π/n)

 As n approaches infinity, s approaches r, and the area approaches:

0.5 * infinity * r² * cot(π/infinity)

= 0.5 * infinity * r² * 1

= πr²

the area of the circle.

Applications 

While it may seem like an abstract question, pondering the number of sides a circle has can have implications and applications in several fields:

Mathematics and Geometry

Understanding the concepts of sides and vertices is fundamental to exploring more complex shapes and structures. The concept of a circle having an infinite number of sides can be a stepping stone to understanding the idea of limits, integral calculus, and the principles of continuity.

Physics and Engineering

The notion of a circle having one side or an infinite number of sides can be applicable in physics, particularly in the study of optics and mechanical engineering. The behavior of light as it refracts and reflects can be analyzed by treating the interface as an infinitesimally small section of a circle.

Similarly, understanding the characteristics of a wheel (which is circular) as an object with infinite contact points aids in the analysis of friction and motion.

Computer Graphics and Animation

In the field of computer graphics and animation, circles and other curved shapes are often modeled as polygons with many sides to approximate a smooth surface. The more sides the polygon has, the more the shape will appear as a perfect circle. This approach is crucial for rendering realistic images and animations.

Architecture and Design

In architecture, circles are often used because of their unique properties, which can be tied back to the concept of sides. For instance, the understanding that a circle has no sides or corners can influence the design of structures and spaces where wind resistance is crucial or where a sense of equality (no point on the boundary is different from any other) is desired.

The absence of distinct sides or corners in a circle can provide a smooth and harmonious aesthetic that architects may seek to incorporate into their designs.

Teaching and Learning

This question can serve as a great pedagogical tool. It helps to challenge students’ understanding and assumptions about shapes, pushing them to think critically and deeply about seemingly simple concepts.

By exploring different perspectives and interpretations, students can develop a stronger grasp of geometric principles and enhance their critical thinking skills.

Surveying and Map Making

Cartographers and surveyors often break down the curved surface of the Earth into small polygons for more manageable calculations. Although it’s more accurate to consider the Earth’s surface as a sphere (a three-dimensional analogue to a circle), treating it as a polyhedron with many flat faces simplifies the mathematics involved.

Astronomy

The orbits of planets and other celestial bodies are often approximated as circles. While Kepler’s first law of planetary motion states that planets orbit the Sun in elliptical paths, these ellipses are very close to circles for most planets. The concept of a circle as a shape with an infinite number of sides can help in calculating the paths of these orbits.

Computer Science and Algorithms

In computer algorithms related to graphics, a circle is often rendered as a polygon with many sides. The Bresenham’s Circle Drawing Algorithm, for instance, is a way of approximating the pixels needed to create the illusion of a circle on a pixelated screen.

Geology and Seismology

When an earthquake occurs, the seismic waves spread out in all directions, creating a ripple effect similar to dropping a stone in a pond. The concept of a circle having infinite sides helps in predicting how these waves propagate and how they will affect different regions.

Sport Sciences

In sports like soccer or basketball, understanding the dynamics of a ball, which is spherical, involves the concept of a circle in three dimensions. For instance, understanding the spin of a basketball during a shot or the curve of a soccer ball during a free kick can be linked back to the concept of a circle and its properties.

Civil Engineering and Urban Planning

Traffic roundabouts are designed using the principles of a circle. Understanding the circle’s properties, such as having no corners (or infinitely many, depending on perspective), aids in facilitating the smooth flow of traffic and reducing the risks of accidents.

Remember that the concept of how many sides a circle has is largely philosophical and theoretical. However, these interpretations provide different perspectives that can be applied to understand and solve real-world problems.

Circle as a Limit of Polygons

The idea of a circle as a limit of polygons indeed comes from the realm of calculus, particularly the concept of a limit, which is a value that a function or sequence “approaches” as the input or index approaches some value. In the case of a circle, you can approximate a circle by inscribing or circumscribing it with regular polygons (polygons with all sides and angles equal) and then increasing the number of sides of these polygons.

Inscribing Polygons

Start with a circle and draw a regular polygon inside it, such that all vertices of the polygon touch the circle. Now, as the number of sides of the inscribed polygon increases, the polygon starts looking more and more like a circle.

The more sides the polygon has, the closer its area and perimeter come to the area and circumference of the circle. If you were to inscribe a polygon with an infinite number of sides, it would “become” the circle.

Circumscribing Polygons

Conversely, you can also start by drawing a regular polygon around the circle, such that all sides of the polygon are tangent to the circle. As the number of sides increases, the polygon will look more and more like the circle, and the circle can be seen as the limit of such polygons as the number of sides tends to infinity.

This concept, where regular polygons with an increasing number of sides tend to become a circle, is an application of the mathematical concept of limits. It forms the basis of many calculations involving circles, particularly the computation of pi (π), where ancient mathematicians like Archimedes inscribed and circumscribed polygons to approximate the value of π.

In modern calculus, this concept is used in the technique of Riemann sums to calculate areas under curves and in integral calculus. It’s essential to note that a polygon will never actually become a circle, no matter how many sides it has.

However, the properties of the polygon (like its area and perimeter) will tend to the properties of the circle (its area and circumference), providing a useful mathematical model for understanding and calculating the properties of circles.

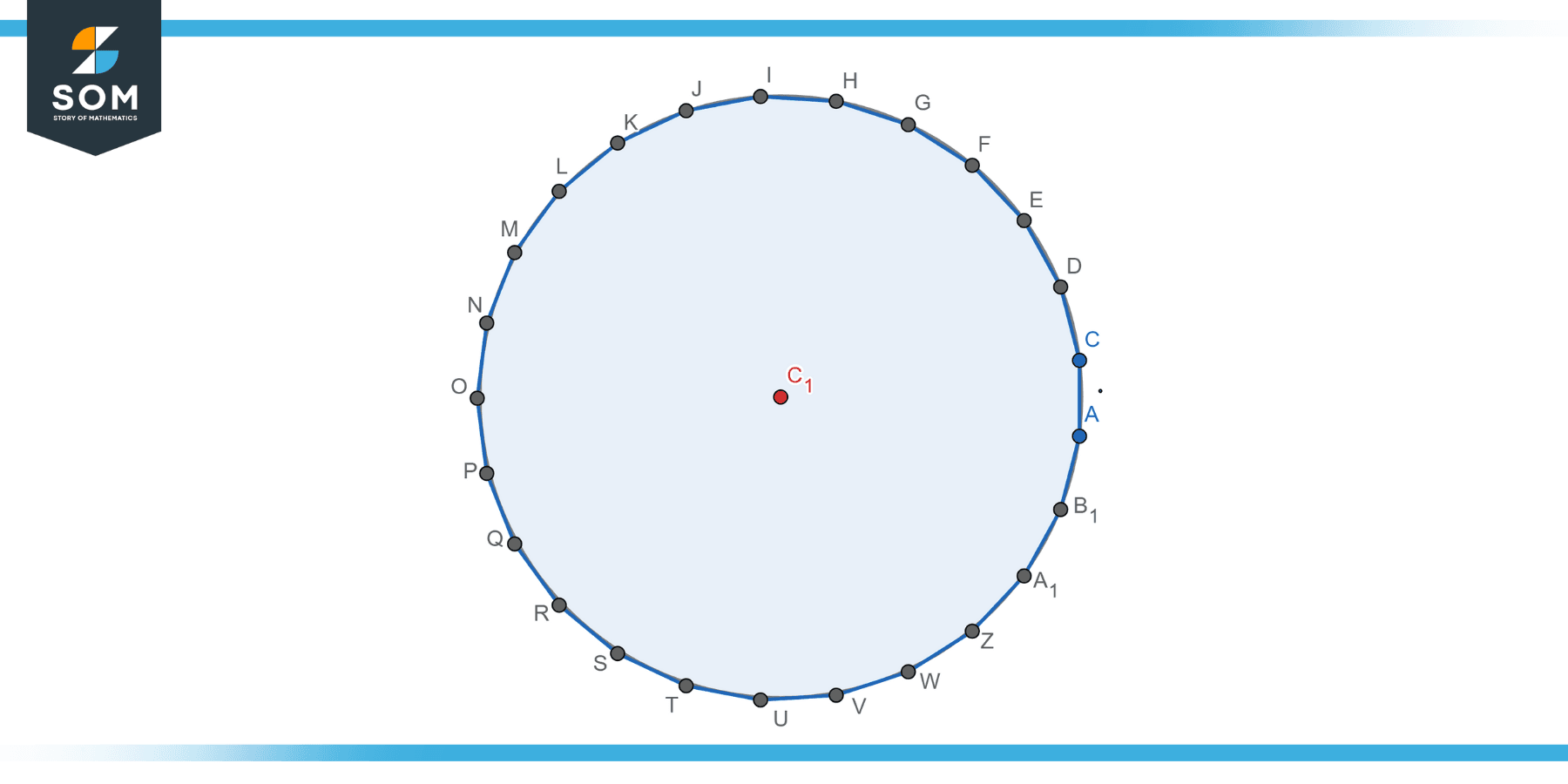
Figure-7.

Historical Significance

The history of contemplating the nature of a circle and its sides dates back to ancient civilizations and forms the basis for much of our understanding of geometry today.

Ancient Egypt

The Rhind Mathematical Papyrus, dating from around 1800 BC, shows that the ancient Egyptians used a simple approximation for the area of a circle, treating it in a way similar to a square. This approach doesn’t directly engage with the question of how many sides a circle has, but it suggests an early attempt to grapple with the circle’s unique nature.

Ancient Greece

The ancient Greeks made significant progress in understanding circles. Greek mathematicians like Euclid, in his monumental work “Elements,” treated circles as having no sides, distinct from polygons, which have a finite number of sides.

However, it was also the Greeks, particularly the mathematician and philosopher Zeno of Elea, who first contemplated the paradoxical nature of infinity, which underpins the idea of a circle having an infinite number of sides.

Archimedes

Around 250 BC, the Greek mathematician Archimedes made a significant breakthrough by closely approximating the value of π (pi), the ratio of a circle’s circumference to its diameter.

He did this by inscribing and circumscribing polygons with many sides around a circle and calculating their perimeters. This method indirectly considered a circle as having an infinite number of sides, forming the basis for our modern understanding of limits in calculus.

Islamic Golden Age

In the Islamic Golden Age (8th to 14th centuries), scholars continued the Greek tradition of mathematical inquiry, further exploring the properties of circles and spheres in the context of astronomy and geometry. This work also contributed indirectly to the understanding of a circle’s “sides.”

Modern Age

The development of calculus in the 17th century by Newton and Leibniz solidified the concept of a circle having an “infinite number of sides.” With calculus, mathematicians could precisely handle the concept of infinity, which is key to understanding a circle as a limit of polygons with increasing numbers of sides.

In summary, the question “How many sides does a circle have?” has deep roots in mathematical history. Different answers to this question reflect various attempts to understand the unique and intriguing nature of the circle. These historical perspectives continue to shape our modern understanding of geometry and the nature of shapes.  

All images were created with GeoGebra.