How to Find the Intersection of Two Planes – A Comprehensive Guide

Geometry plays a crucial role in our understanding of the physical world. In advanced geometry, particularly in three-dimensional space, planes are infinite flat surfaces that extend indefinitely in all directions.

How to find the intersection of two planes? This article delves into the methods of finding the intersection of two planes and the significance of the intersection line.

How to Find the Intersection of Two Planes

To find the intersection of two planes, we solve their equations simultaneously. The intersection can be a line (given as a point and a direction) or can be the entire plane (if they’re identical) or no intersection (if they’re parallel).

To further understand the concept, we need to delve into the understanding of planes first, let us begin with some fundamentals of a plane.

Introduction to Planes

In three-dimensional space, a plane can be defined using a point and a normal vector to the plane or using three non-collinear points. The equation of a plane is generally represented in the form:

$ax+by+cz=d$

Where $a,b,c$ are the coefficients of the normal vector to the plane and $d$ is a constant.

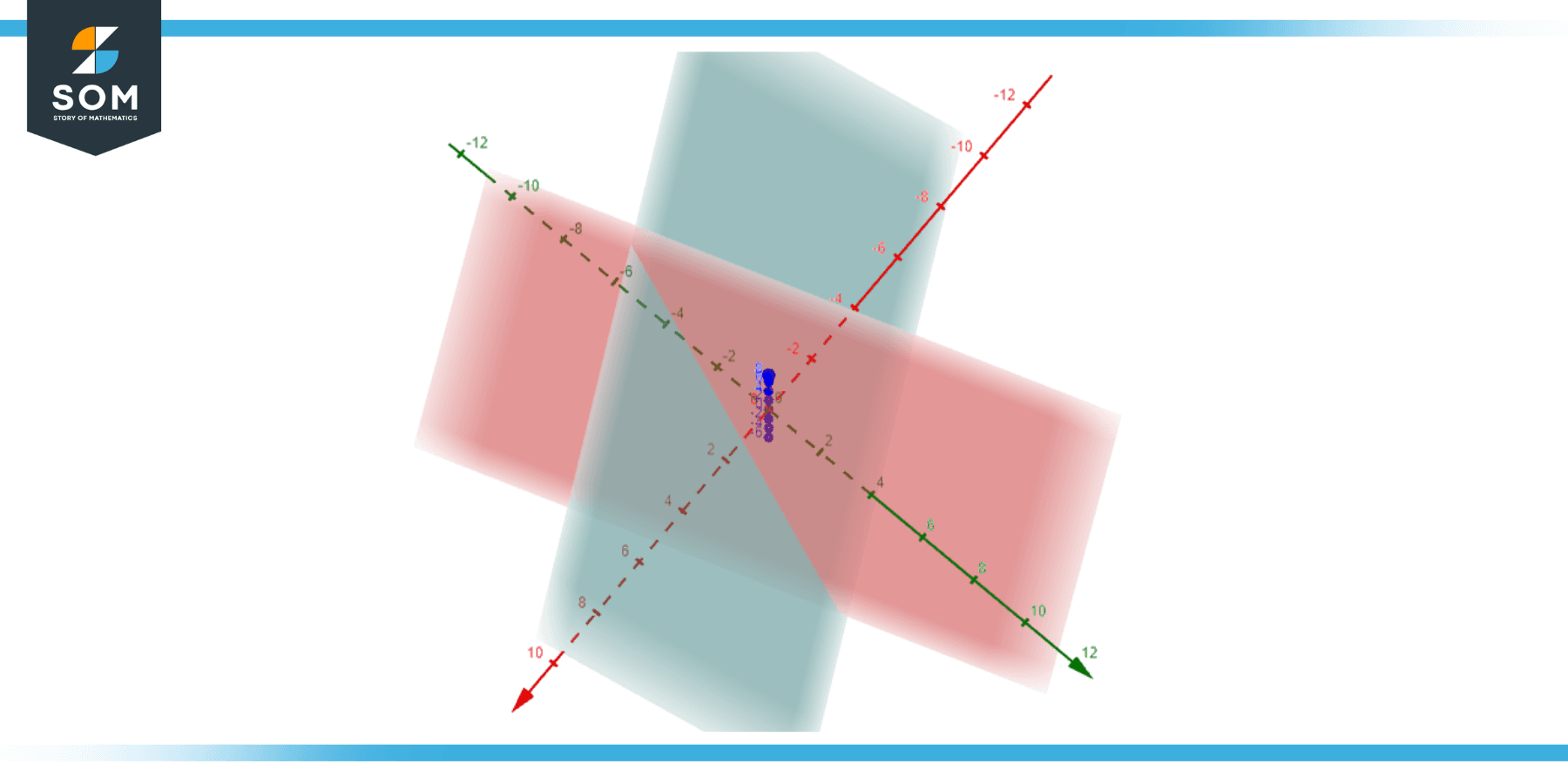
Figure-1.

Understanding Intersections

When two planes intersect, they typically do so along a straight line, unless they are parallel. This intersection line will have its unique direction vector, determined by the cross product of the normal vectors of the two planes.

However, if two planes are parallel and distinct, they won’t intersect. If they are coincident (i.e., the same plane), then their intersection is the plane itself.

Finding the Intersection of Two Planes

• Determine the Direction Vector of the Line of Intersection

  • Begin by identifying the normal vectors of the two planes. If your planes are defined by the equations:

a1 * x + b1 * ​y + c1 * ​z = d1​

a2 ​* x + b2 * ​y + c2 * ​z = d2​

The normal vectors are n1 ​= <a1​, b1​, c1​> and n2 = <a2​, b2​, c2​>.

• • Calculate the direction vector of the intersection line $\text{d}$, by taking the cross product of n1n1​ and n2n2​.

• Find a Point on the Line of Intersection

One approach is to set one of the variables (x, y, or z) to a constant value, then solve the two plane equations simultaneously to get the values of the other two variables. This will give you a point on the intersection line.

• Determine the Parametric Equations

 With the direction vector $\text{d}$ and a point P(x0​ ,y0​, z0​) on the line, the parametric equations of the intersection line can be expressed as:

x = x0​ + d * t1

​y = y0 ​+ d * t2​

z = z0 ​+ d * t3​

Where $t$ is a parameter and (t1​, t2​, t3​) are the components of the direction vector $\text{d}$.

Exercise

Example 1

Plane 1: $x+y+z=6$
Plane 2: $x-y+z=2$

Solution

To find their intersection, equate z from both equations:
From Plane 1: $z=6-x-y$
Substitute in Plane 2: $x-y+6-x-y=2$
This gives: $-2y=-4$
Thus, $y=2$
Now, using $y=2$ in Plane 1: $x+2+z=6$ => $x+z=4$
So, the intersection line is: $x+z=4$, and $y=2$.

Example 2

Plane 1: $2x-3y+z=5$
Plane 2: $x+y-z=1$

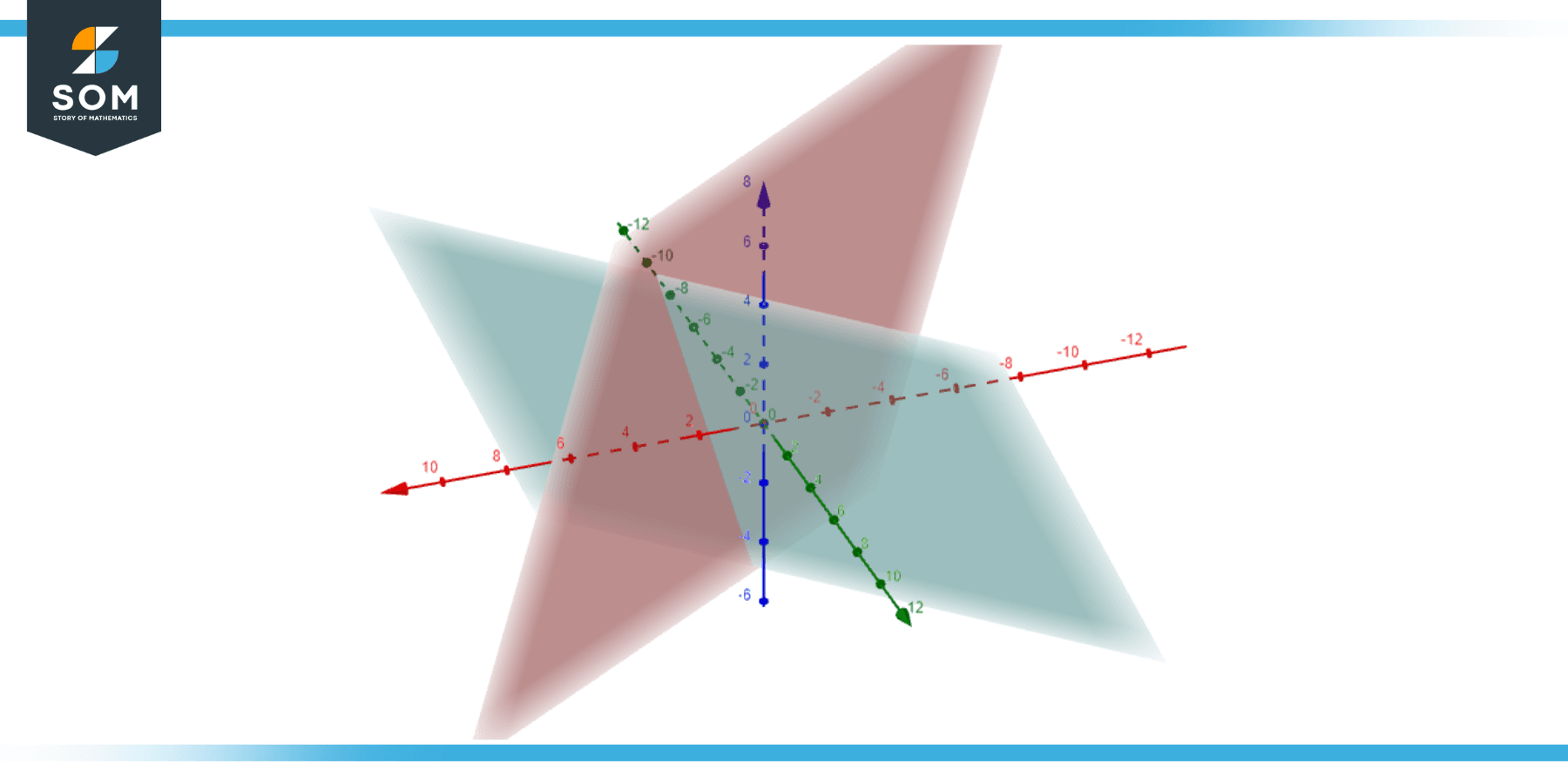
Figure-2.

Solution

Equating z from both:
From Plane 1: $z=5-2x+3y$
Substitute in Plane 2: $x+y-5+2x-3y=1$
This yields: $3x-2y=6$.
Using Plane 1 for z: $z=5-2x+3y$
Intersection line is described by: $3x-2y=6$, and $z=5-2x+3y$.

Example 3

Plane 1: $3x-y-2z=7$
Plane 2: $x+2y-z=2$

Solution

From Plane 1: z = (3x − y − 7)/2​
Substitute in Plane 2: x+2y− (3x − y − 7)/2 ​= 2
This results in: $y=-x+3$
Using Plane 1 for z: z = (3x − y − 7)/2​
Intersection line: $y=-x+3$, and z = (3x − y − 7)/2​

Example 4

Plane 1: $x-y+z=2$
Plane 2: $2x+y+3z=6$

Solution

From Plane 1: $z=2-x+y$

Substitute in Plane 2: $2x+y+3(2-x+y)=6$
This simplifies to: $x+4y=0$

Using Plane 1 for z: $z=2-x+y$

Intersection line: $x+4y=0$, and $z=2-x+y$.

Example 5

Plane 1: $3x+y+z=4$
Plane 2: $x-2y-z=1$

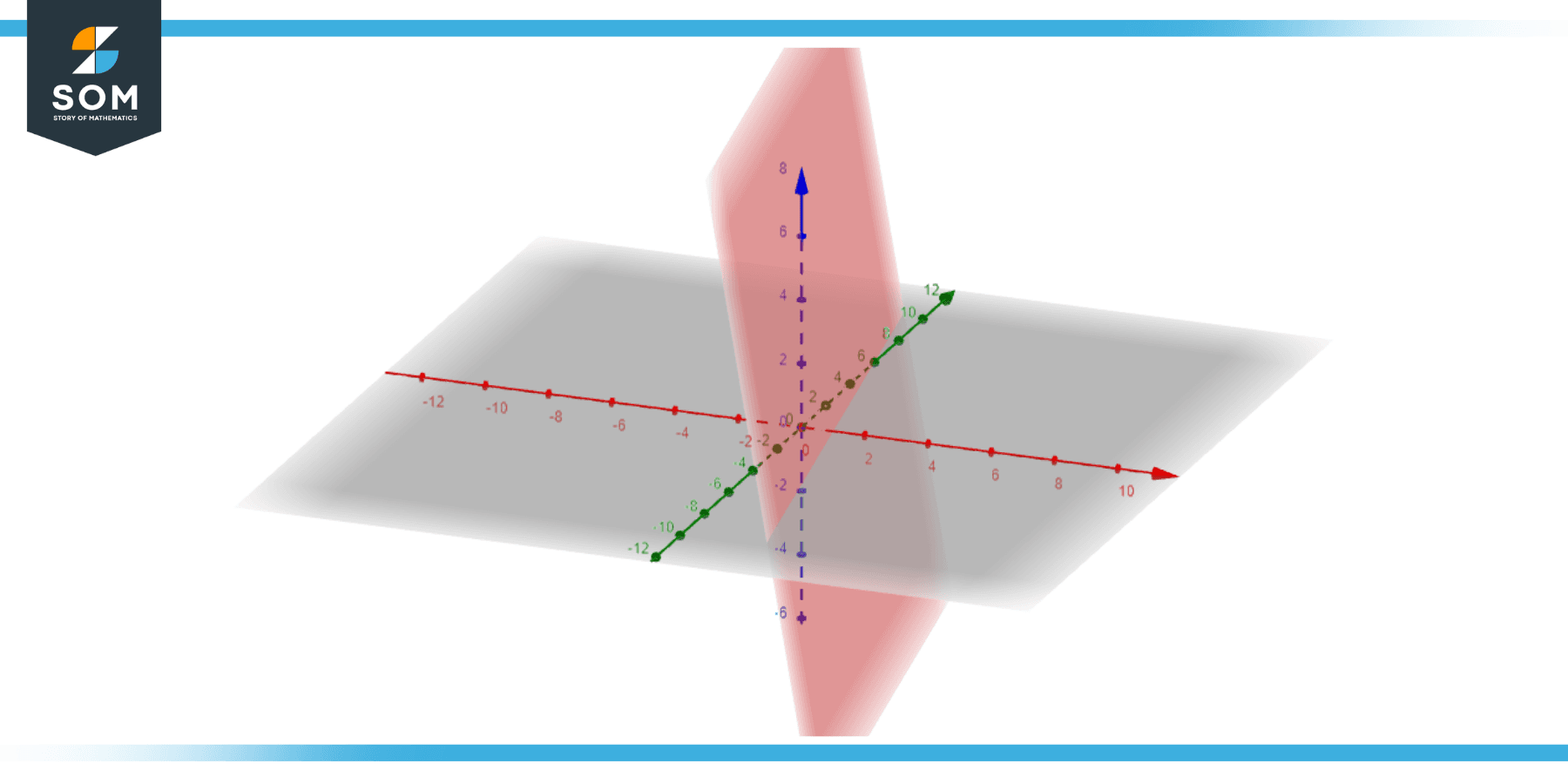
Figure-3.

Solution

From Plane 1: $z=4-3x-y$

Substitute into Plane 2: $x-2y-4+3x+y=1$
This gives: $4x-y=5$

Using Plane 1 for z: $z=4-3x-y$

Intersection line: $4x-y=5$, and $z=4-3x-y$.

Real-World Implications of Finding the Intersection of Two Planes

The mathematical principle of determining the intersection of two planes might seem abstract, but its real-world applications abound across various fields. Unraveling where two planes meet is essential in numerous sectors, be it technology, engineering, design, or even natural phenomena. Here’s a look at how this geometric concept integrates seamlessly into our daily lives.

• Civil Engineering and Architecture

  • In the design and construction of infrastructure, understanding where two planes intersect helps in determining stress points, especially in complex structures.
  • For architects, intersections can form design features, such as where the roof meets a wall, or how multi-level terraces might interact with each other.

• Computer Graphics and Animation

  • Rendering realistic environments often requires determining where surfaces meet, which is essentially calculating the intersection of planes. Shadows, reflections, and even character interactions might be based on these calculations.
  • Gaming environments, where characters navigate complex terrains, interact with objects, or when objects crash into each other, rely on intersection calculations.

• Air Traffic Control

  • Air traffic controllers ensure that aircraft maintain safe distances from each other. In a three-dimensional airspace, flight paths can be considered as planes. Recognizing potential intersections helps in preventing mid-air collisions.

• Geology and Geography

  • Studying the Earth’s layers, especially during phenomena like plate tectonics, can be understood in terms of plane intersections. For instance, where two tectonic plates meet (converge), mountain ranges or deep ocean trenches can form.
  • In topographical mapping, the intersection of planes can represent ridgelines or river valleys.

• Astronomy

  • The study of celestial mechanics, especially when plotting the orbits of planets and other celestial bodies, can involve understanding the points where orbits (considered as planes in space) intersect.
  • Phenomena like eclipses occur when the planes of orbits of the Earth and the Moon intersect, casting shadows on each other.

• Medicine

  • In medical imaging, like MRI or CT scans, images are taken in slices or planes. To understand a three-dimensional structure or locate a tumor, radiologists might look at the intersections of these planes.

• Design and Art

  • Sculptors, especially those working with materials like stone or metal, need to understand the intersection of planes to shape their artwork correctly.
  • In graphic design, understanding how two planes interact can aid in creating depth, perspective, and layers in an artwork.

• Marine Navigation

  • Just like in air traffic, ship navigators need to be aware of potential intersections with other vessels, especially in busy shipping lanes or narrow straits. This becomes even more crucial in foggy conditions or at night.

• Meteorology

  • The study of weather patterns, particularly fronts (where warm and cold air masses meet), can be conceptualized as the intersection of two planes. These intersections often result in weather events like thunderstorms or shifts in wind patterns.

• Economics and Market Research

  • Believe it or not, even in economics, the concept of plane intersections is used. For instance, in graphical methods, the intersection of supply and demand curves (which can be thought of as planes in multi-variable scenarios) determines equilibrium price and quantity.

All images were created with GeoGebra.