JUMP TO TOPIC

This article aims to provide an in-depth exploration of the concept of ln(0), demystifying its nature, its undefined status in real numbers, and its implications within the field of mathematics.
Delving into the mathematical fabric that constitutes this unique expression, we aspire to bring clarity and understanding to this compelling aspect of logarithmic functions.
Definition
Regarding ln(0), the natural logarithm function is undefined for zero or any negative number in the real number system. This is because there is no real number that you can raise ‘e’ to get zero or a negative number.
The natural logarithm function, denoted as “ln,” is the inverse of the exponential function with base ‘e,’ where ‘e’ is approximately equal to 2.71828. The natural logarithm of a number ‘x’ is denoted as ln(x) and is defined for all positive real numbers.
In mathematical terms, if you graph y = ln(x), the graph would approach negative infinity as ‘x’ approaches zero from the right. So, for real numbers, we say that ln(0) is undefined or negative infinity.
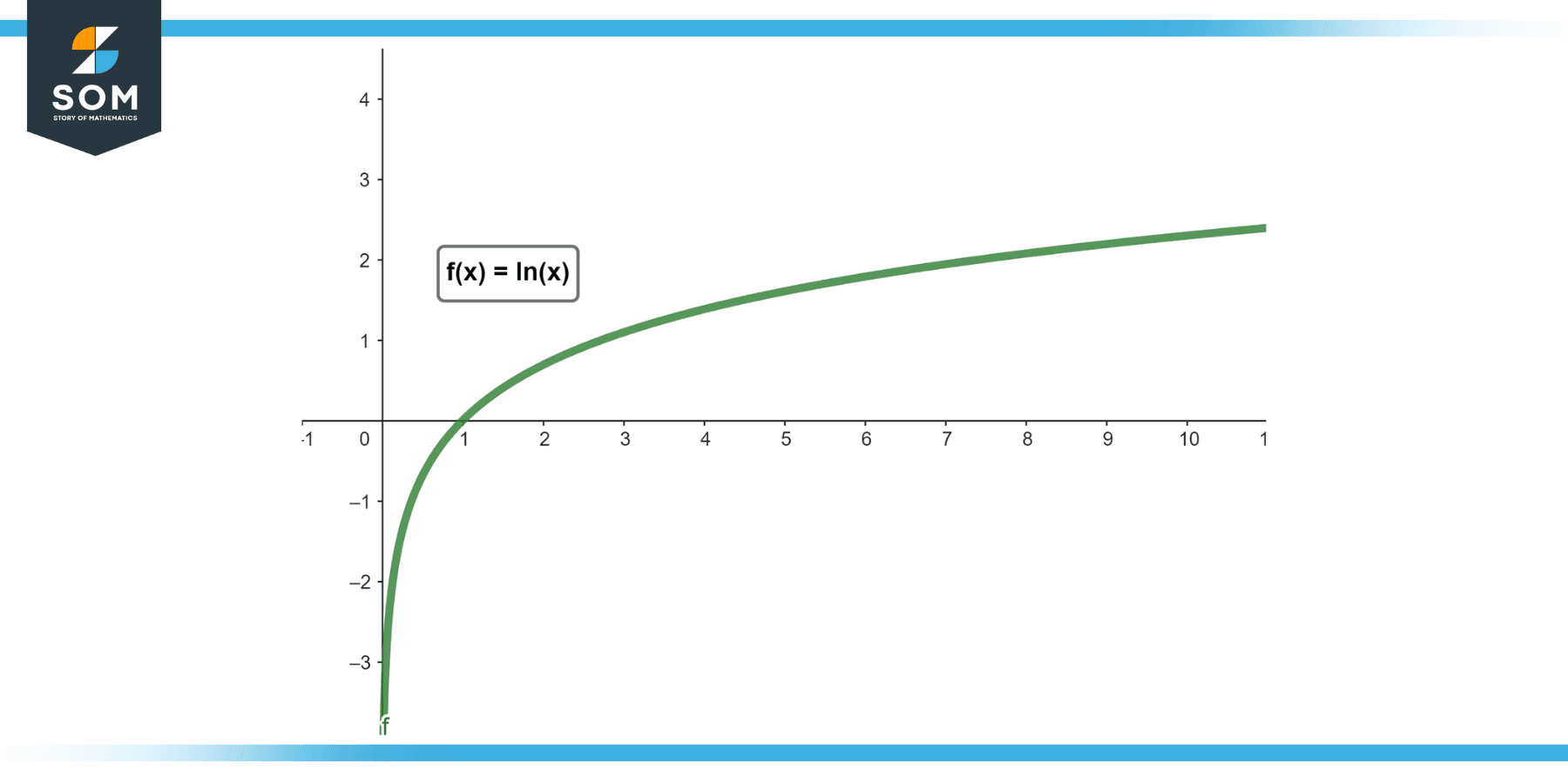
Figure-1.
However, in the complex number system, there are complex values ‘z’ for which $e^z$ = 0 can hold, but these cases extend beyond the realm of real numbers and venture into the more advanced topic of complex analysis.
Properties
Here are some key properties and features:
Undefined in Real Numbers
ln(0) is undefined in the set of real numbers because there is no real number ‘x’ for which $e^x$ = 0.
Negative Infinity in Limit Terms
In terms of limits, we often say that ln(x) approaches negative infinity as x approaches 0 from the right (x → 0+), symbolically written as $lim_{x→0+}$ ln(x) = -∞. The y = ln(x) graph descends without bounds as ‘x’ gets closer to 0.
Complex Logarithms
In the realm of complex numbers, the natural logarithm can be defined for negative numbers and zero, but it involves complex infinity and complex analysis, which is a more advanced topic.
Continuity and Differentiability
The function y = ln(x) is continuous and differentiable for all x > 0. However, it’s neither continuous nor differentiable at x = 0, and as such, ln(0) is not a value that fits into the normal rules of calculus.
Monotonic Function
The function y = ln(x) is a strictly increasing function for x > 0. This means that as ‘x’ increases, ln(x) also increases. This is true up to x approaching 0 from the right, where ln(x) approaches negative infinity.
Exercise
Example 1
Calculate $lim_{x→0+}$ ln(x).
Solution
The limit of ln(x) as x approaches zero from the right is negative infinity. So, $lim_{x→0+}$ ln(x) = -∞.
Example 2
Calculate $lim_{x→0+}$ x ln(x).
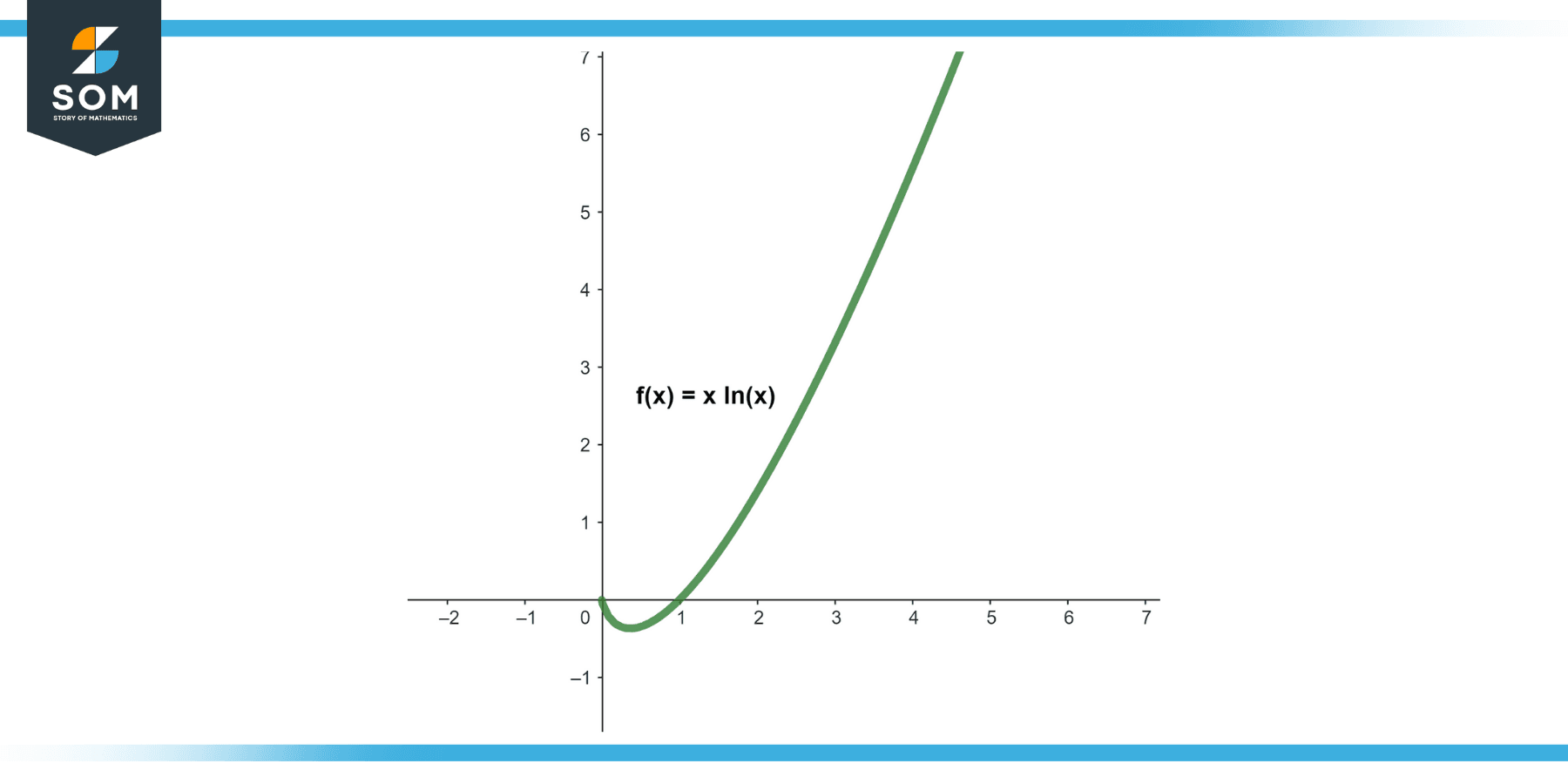
Figure-2.
Solution
This is an indeterminate form of type 0*(-∞). By applying L’Hopital’s rule (which states that this limit is the same as the limit of the ratio of the derivatives), we get:
$lim_{x→0+}$ [1 / (1/x)]
= $lim_{x→0+}$ x
= 0
Example 3
Calculate the derivative of ln(x) at x=0.
Solution
The derivative of ln(x) is 1/x, but x=0 is undefined, demonstrating again that ln(x) is not differentiable at x=0.
Example 4
Calculate $lim_{x→0+}$ ln(1/x).
Solution
This limit can be simplified using the property ln(1/x) = -ln(x), thus:
$lim_{x→0+}$ ln(1/x)
=$lim_{x→0+}$ -ln(x)
= -$lim_{x→0+}$ ln(x)
= -(-∞)
= ∞
Example 5
Calculate the integral from 1 to ∞ ln(x) / x dx.
Solution
This integral also involves ln(x) near zero from the perspective of a very large x. Because ln(x) grows more slowly than x, this integral converges to a finite value (specifically, Euler’s constant, γ), demonstrating the slow growth of ln(x).
Example 6
Calculate $lim_{x→0+}$ ln(sin(x)).
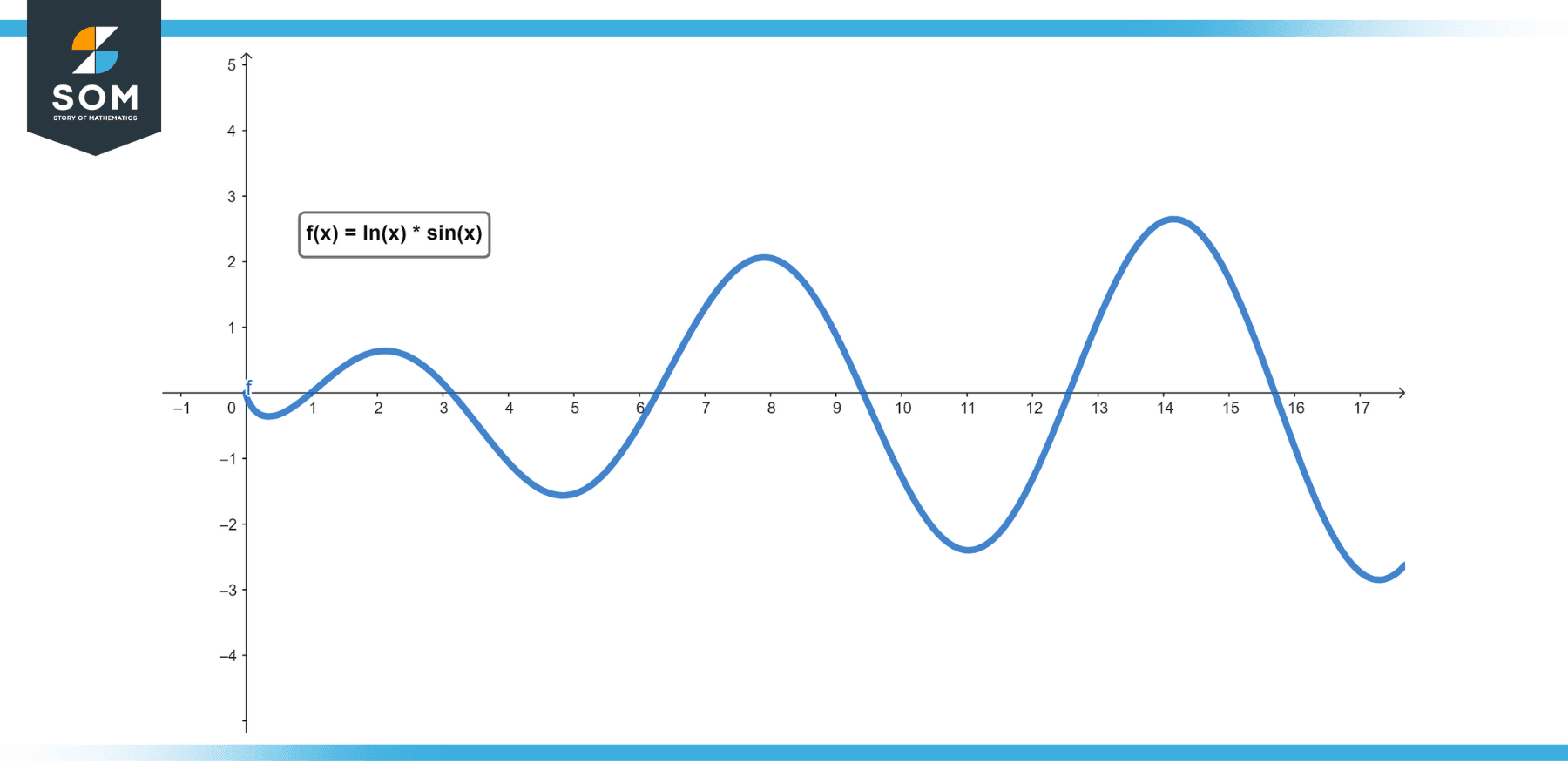
Figure-3.
Solution
Here we can use the limit property that if l $lim_{x→a}$ f(x) = lim_(x→a) g(x) = L, then $lim_{x→a}$ f(g(x)) = f(L). We know that $lim_{x→0+}$ sin(x) = 0, and we can apply this property here to get:
$lim_{x→0+}$ ln(sin(x))
= ln($lim_{x→0+}$ sin(x))
= ln(0)
undefined in the real number system.
Applications
Calculus and Mathematics
Understanding the behavior of ln(x) as x approaches 0 is essential in calculus, particularly in limit problems, differential calculus, integral calculus, and series expansion.
Complex Analysis
The natural logarithm can be extended to the complex number plane. While ln(0) is still a troublesome point (and it is often said to be “complex infinity”), understanding how to extend logarithms to complex arguments requires grappling with the behavior at zero.
Computer Science and Information Theory
In computer science, especially in data compression and information theory, the concept of logarithms and understanding their behavior around zero is fundamental. For instance, Shannon’s entropy formula – a key concept in information theory – involves the log function, and understanding its behavior as the argument approaches zero is important.
Physics
Natural logarithms come into play in physics, particularly in thermodynamics and quantum mechanics. Understanding the behavior of ln(x) as x approaches zero can be essential in these contexts, such as understanding entropy or the behavior of gases.
Economics and Finance
In economics, natural logarithms are used to model growth and to calculate compound interest. The notion of continuous compounding can be thought of in terms of $e^x$ and its inverse, ln(x), and understanding these functions’ behavior near zero can be important in such contexts.
Statistics and Machine Learning
Natural logarithms are used in various methods and algorithms in statistics and machine learning. They’re integral to calculations involving probabilities, especially in the context of logistic regression, likelihood functions, and information criteria like AIC and BIC.
While ln(0) is undefined, understanding the behavior of the function ln(x) near zero and handling expressions where the argument approaches zero, often through limits or similar constructions, is critical in these and other fields.
All images were created with GeoGebra.
