Inverse Variation – Explanation & Examples

Inverse variation means that a variable has an inverse relationship with another variable, i.e., the two quantities are inversely proportional or varies inversely to each other. Mathematically, it is defined by the relation $y = \dfrac{c}{x}$, where $x$ and $y$ are two variables and $c$ is a constant.

Two quantities $x$ and $y$ are said to be in an inverse relation when $x$ increases if $y$ decreases and vice versa.

What Is Inverse Variation?

Inverse variation is a mathematical relation that shows the product of two variables/quantities is equal to a constant.

$x.y = c$

$y = \dfrac{c}{x}$

Inverse Variation Between Two Variables

The inverse relation between two variables or quantities is represented through inverse proportion. The previous example $y = \dfrac{4}{x}$ is between two variables “x” and “y”, which are inversely proportional to each other.

We can also write this expression as:

$xy =4$

In the above table for each case, the product xy = 4, justifying the inverse relation between the two variables.

Inverse Variation Formula

Inverse variation states that if a variable $x$ is inversely proportional to a variable $y$, then the formula for inverse variation will be given as:

  $y \propto \dfrac{1}{x}$

$y = \dfrac{c}{x}$

If we are given two different values of $x$, say $x_1$ and $x_2$ and let $y_1$ and $y_2$ be the corresponding values of $y$, then the relation between the pair $(x_1,x_2)$ and $(y_1,y_2)$ is given as:

$\dfrac{x_1}{x_2} = \dfrac{y_2}{y_1}$

Visualization

To visualize an inverse relation, lets put $c$ equals $4$, and the graphical representation of the formula $y = \dfrac{4}{x}$ is as shown below:

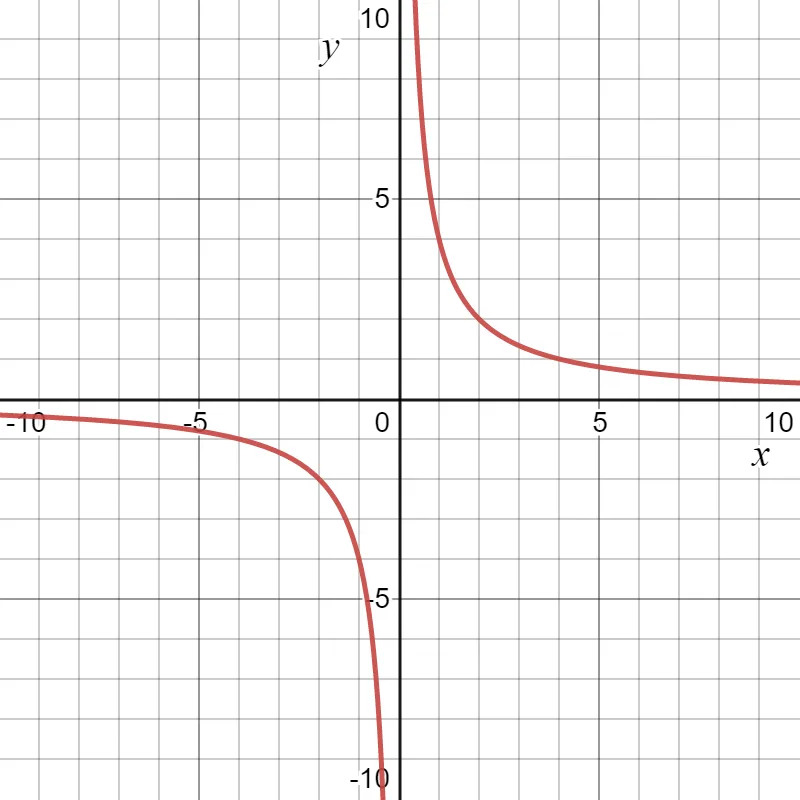
We can see from the above table that an increase (or decrease) in the value of $x$ will result in a decrease (or increase) in the value of $y$.

In a mathematical relation, we have two types of variables: the independent and the dependent variable. As the name suggests, the value of the dependent variable is dependent upon the value of the independent variable.

If the value of the dependent variable varies in such a way that, if the independent variable increases then the dependent variable decreases and vice versa, then we say an inverse variation exists between these two variables. We can observe the inverse variation phenomenon in our daily life.

Let’s discuss some real-life examples below:

1.  We can observe an inverse variation relation while driving a car. For example, let’s say you have to move from location A to B. Here, the time to cover the whole distance and the speed of the car has an inverse relation. The higher the vehicle’s speed, the less time it would take to reach location B from A.

2.  Similarly, the time it takes to complete a labor work and the number of laborers have an inverse relation between them. The larger the number of laborers, the lesser time it would take to complete the work.

In this topic, we will learn and understand the inverse variation with graphical representation, its formula, and how it is used, along with some numerical examples.

How To Use Inverse Variation

Inverse variation is simple to calculate if only two variables are given.

1. Write down the equation $x.y = c$
2. Calculate the value of constant $c$
3. Rewrite the formula in fraction form $y = \dfrac{c}{x}$
4. Insert different values of independent variables and draw the inverse relation graph between these two variables.

Example 1: 

If a variable $x$ varies inversely to a variable $y$, calculate the value of the constant $c$ if $x$ = $45$  has $y$ = $9$. Also, find the value of $x$ when the value of $y$ is $3$.

Solution:

We know that product of two variables in an inverse relation is equal to a constant.

$x.y = c$

$45\times 9 = c$

$c = 405$

Now we have the value of the constant $c$ so we can calculate the value of $x$ if $y = 3$.

The variable $x$ is inversely proportional to $y$

$x = \dfrac{c}{y}$

$x = \dfrac{405}{9}$

$x = 45$

Example 2: 

If a variable $y$ varies inversely to a variable $x$, calculate the value of the constant $c$ when $x$ = $15$  then $y$ = $3$. Also, find the value of $x$ if the value of $y$ is $5$.

Solution:

We know that product of two variables in an inverse relation is a constant.

$x.y = c$

$15\times 3 = c$

$c = 45$

Now we have the value of constant $c$ so we can calculate the value of $x$ if $y = 25$.

The variable $y$ is inversely proportional to $x$

$y = \dfrac{c}{x}$

$25 = \dfrac{45}{x}$

$x = \dfrac{45}{5}$

$x = 9$

Example 3:

If a variable $x$ is inversely proportional to a variable $y$, then for the given table, calculate the value of the variable $y$ for given values of variable $x$. The value of constant $c$ is known to be $5$.

Solution:

The variable $x$ is inversely proportional to variable $y$, and the value of constant is $5$. Hence, we can write the equation for calculating $x$ for different values of $y$.

$x = \dfrac{5}{y}$

So, by using the above equation we can find out all the values of variable $x$.

Example 4: 

If 12 men can finish a task in 6 hours, how long will it take 4 men to finish the same task?

Solution:

Let men =$ x$ and hours = $y$

So, $x_1 = 12$ , $x_2 = 4$ and $y_1 = 6$

We have to find the value of $y_2$.

We know the formula:

$\dfrac{x_1}{x_2} = \dfrac{y_2}{y_1}$

$\dfrac{12}{4} = \dfrac{y_2}{6}$

$3 = \dfrac{y_2}{6}$

$y_2 = 3\times 6$

$y_2 = 18$ hours

This means that $4$ men will take $18$ hours to finish the task.

Example 5: 

A charity is providing food for homeless people. The charity has arranged food for $15$ days for $30$ people. If we add $15$ more people to the total, how many days will the food last for $45$ people?

Solution:

Let people = $x$ and days = $y$

So $x_1 = 30$ , $x_2 = 45$ and $y_1 = 15$

We have to find the value of $y_2$.

We know the formula:

$\dfrac{x_1}{x_2} = \dfrac{y_2}{y_1}$

$\dfrac{30}{45} = \dfrac{y_2}{15}$

$\dfrac{2}{3} = \dfrac{y_2}{15}$

$y_2 = (\dfrac{2}{3}) 15$

$y_2 = 10$ days

Example 6: 

Adam is distributing ration for victims of war. He has $60$ people under his supervision. The current ration storage can last for $30$ days. After $20$ days, $90$ more people are added under his supervision. How long will the ration last after this addition of new people?

Solution:

Let people = x and days = y

We added the new people after $20$ days. We will solve for the last $10$ days and add up the first $20$ days in the end.

So $x_1 = 60$ , $x_2 = 90$ and $y_1 = 10$

We have to find the value of $y_2$.

We know the formula:

$\dfrac{x_1}{x_2} = \dfrac{y_2}{y_1}$

$\dfrac{60}{150} = \dfrac{y_2}{10}$

$\dfrac{6}{15} = \dfrac{y_2}{10}$

$y_2 = (\dfrac{6}{15}) 10$

$y_2 = 6$ days

So the total number of days the ration will last = $20\hspace{1mm} +\hspace{1mm} 6$ = $26$ days.

Inverse Variation With Power

Non-linear inverse variation deals with inverse variation with a power. It is the same as a simple inverse variation. The only difference is that the variation is represented using a power of “n” as follows:

$y \propto \dfrac{1}{x^{n}}$

$y = \dfrac{c}{x^{n}}$

Just like the simple example we saw earlier for graphical representation, let us take the value of $c$ equal to 4. Then the graphical representation of $y$ being inversely proportional to $x^{2}$, $y = \dfrac{4}{x^{2}}$ can be plotted as shown below:

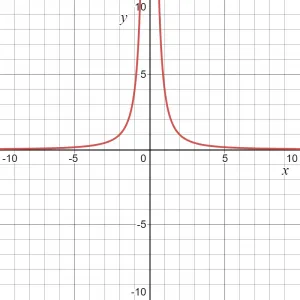
Example 7: 

If the variable $y$ is inversely proportional to the variable $x^{2}$, clculate the value of the constant $c$, if for $x$ = $5$ we have $y$ = $15$. Find the value of $y$ if the value of $x$ is $10$.

Solution:

$x^{2}.y = c$

$5^{2}.15 = c$

$25\times 15 = c$

 $c = 375$

Now we have the value of the constant $c$ so we can calculate the value of $y$ if $x = 10$.

The variable $y$ is inversely proportional to $x^{2}$

$y = \dfrac{c}{x^{2}}$

$y = \dfrac{375}{10^{2}}$

$y = \dfrac{375}{100}$

$y = 3.75$

Practice Questions:

1. If 16 workers can build a house in 20 days, how long will it take 20 workers to build the same house?
2. If the variable $x$ is inversely proportional to the variable $y^{2}$, calculate the value of the constant $c$, if for $x = 15$  we have $y = 10$. Find the value of $x$ if the value of $y$ is $20$.
3. A 6-member group of an engineering class completes an assigned task in 10 days. If we add two more group members, how much time will the group take to finish the same job?

Answer Key:

1.

Let worker = $x$ and days = $y$

So $x_1 = 16$ , $x_2 = 20$ and $y_1 = 20$

We have to find the value of $y_2$.

We know the formula:

$\dfrac{x_1}{x_2} = \dfrac{y_2}{y_1}$

$\dfrac{16}{20} = \dfrac{y_2}{20}$

$y_2 = (\dfrac{16}{20}) 20$

$y_2 = 16$ days

So $20$ workers will build the house in $16$ days.

2.

$x.y^{2} = c$

$15\times 10^{2} = c$

$15\times 100 = c$

$c = 1500$

Now we have the value of the constant $c$ so we can calculate the value of $x$ if $y = 20$.

The variable $x$ is inversely proportional to $y^{2}$

$x = \dfrac{c}{y^{2}}$

$x = \dfrac{1500}{20^{2}}$

$x = \dfrac{1500}{400}$

$x = \dfrac{15}{4}$

3.

Let members = x and days = y

So, $x_1 = 6$ , $x_2 = 8$ and $y_1 = 10$.

We have to find the value of $y_2$

We know the formula:

$\dfrac{x_1}{x_2} = \dfrac{y_2}{y_1}$

$\dfrac{6}{8} = \dfrac{y_2}{10}$

$\dfrac{3}{4} = \dfrac{y_2}{10}$

$y_2 = (\dfrac{3}{4}) 10$

$y_2 = \dfrac{15}{2} = 7.5 days$

So $8$ members will take $7.5$ days to complete all the assignments.