JUMP TO TOPIC
The midpoint theorem highlights how the midpoints of the triangle relate to each other. It also defines how the midsegment formed by the midpoints relates to the third side of the triangle.
In this article, we’ll break down the conditions needed to utilize the midpoint theorem. We’ll break down the theorem, show the proof behind it, and exhibit the interesting properties that can be applied to solve problems.
The discussion assumes one’s understanding of parallel lines, triangle congruency and parallelograms. By the end of this discussion, we want each reader to feel confident when working with triangles, midpoints, and midsegments!
What Is the Midpoint Theorem?
The midpoint theorem is a theorem that states that the line segment formed by the two midpoints of the triangles’ two sides will have a length equal to half of the third side parallel to it. To better understand what the theorem states, take a look at the triangle $\Delta ABC$ shown below.
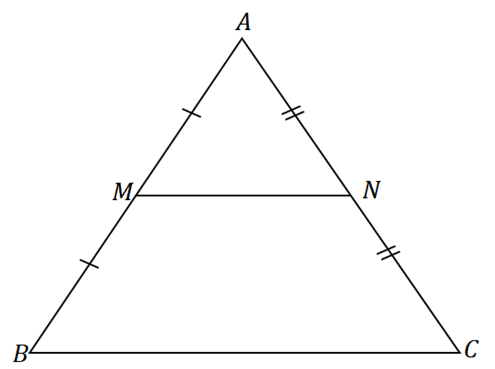
Suppose that $M$ and $N$ are the midpoints of the line segments $\overline{AB}$ and $\overline{AC}$, respectively. Through the midpoint theorem, the following statements are true:
- The line segment $\overline{MN}$ is parallel to the third side of the triangle $BC$.
- The length of $\overline{MN}$ is equal to half that of $\overline{BC}$’s length.
\begin{aligned}\overline{MN} &\parallel \overline{BC}\\\overline{MN} &= \dfrac{1}{2} \overline{BC}\end{aligned}
We call the segment connecting these two midpoints a midsegment. This means that $\overline{MN}$ is the midsegment formed by the midpoints of $\overline{AB}$ and $\overline{AC}$.
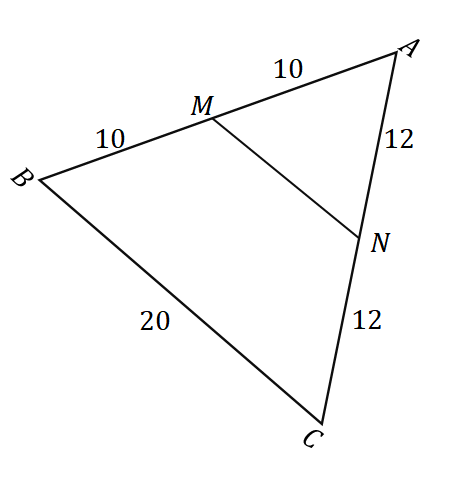
Given the figure shown above, we can apply the midpoint theorem to find the length of the line segment $\overline{MN}$. First, confirm that the points $M$ and $N$ are midpoints of the sides $\overline{AB}$ and $\overline{AC}$. Recall that a midpoint divides a given line segment into two equal parts.
| \begin{aligned}\boldsymbol{M}\end{aligned} | \begin{aligned}\boldsymbol{N}\end{aligned} |
\begin{aligned}\overline{AM} &= \overline{MB}\\&= 10\text{ units}\\\end{aligned} This means that $M$ is indeed a midpoint. | \begin{aligned}\overline{AN} &= \overline{NC}\\&= 12\text{ units}\\\end{aligned} This means that $N$ is indeed a midpoint. |
Once we’ve confirmed that $M$ and $N$ are midpoints, we can confirm that the midpoint theorem applies. This means that when $MN$ and $BC$ are parallel to each other, $\overline{MN} = \dfrac{1}{2} \cdot \overline{BC}$.
\begin{aligned}\overline{MN} &= \dfrac{1}{2} \cdot \overline{BC}\\&= \dfrac{1}{2} (20)\\&= 10\end{aligned}
This means that through the midpoint theorem, it’s now possible to find the length of midsegments such as $\overline{MN}$. To better understand the midpoint theorem, let’s take a look at its proof and learn how to eventually prove other statements using the midpoint theorem.
Understanding the Proof of Midpoint Theorem
To prove the midpoint theorem, use the properties of parallel lines, the definition of parallelograms, and triangle congruency to show the two parts of the midpoint theorem.
These two parts that need to be proven are: 1) that the midsegment is parallel to the third side of the triangle and 2) the midsegment has a length that is half of the third side’s length. To do this, construct line segments to form a triangle adjacent to the triangle.
- Connect another line segment to the midsegment so that the two have equal lengths.
- Construct a line segment so that it is parallel with one of the remaining side’s triangles. This line segment and the one from the previous bullet meets so that they form a triangle.
Applying these steps to the triangle $\Delta ABC$, we’ll have a line segment $\overline{NO}$ that has the same length as the midsegment $\overline{MN}$. In the same figure, construct a line segment $\overline{OC}$ that is parallel to $\overline{AB}$. The resulting figure is as shown below.
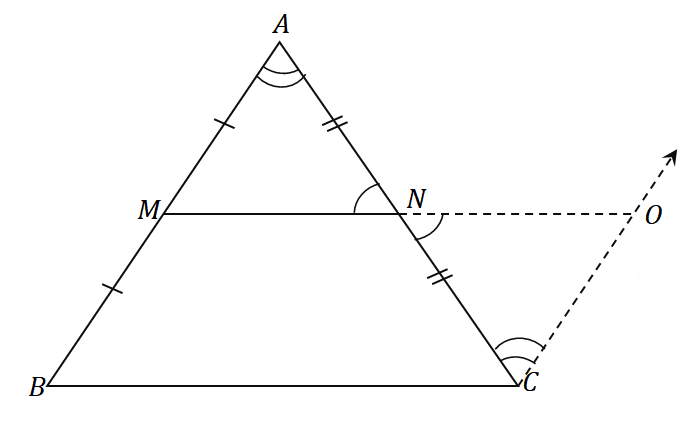
Since $\overline{AB}$ and $\overline{CO}$ are parallel to each other and $\angle ABC$ and $\angle NCO$ are alternate interior angles, these two angles are equal.
Similarly, since $\angle ANM$ and $\angle ONC$ are vertical angles, they share the same angle measurements.
The midpoint $N$ divides the line segment $AC$ equally: $\overline{AN} = \overline{CN}$. By the ASA (Angle-Side-Angle) rule, the triangles $\Delta AMN$ and $\Delta CON$ are congruent. This means that the sides $\overline{AM}$ and $\overline{CO}$ share the same length.
Since $\overline{AM} = \overline{MB}$, by transitive property, $\overline{MB}$ is also equal to $\overline{OC}$.
Since $\overline{MB} = \overline{OC}$ and $\overline{MB} \parallel \overline{OC}$, it is implied that $MBCO$ is a parallelogram.
This confirms the first part of the midpoint theorem:
\begin{aligned} \overline{MO}&\parallel \overline{BC}\\\overline{MN} &\parallel \overline{BC}\end{aligned}
This also means that the line segments $\overline{MO}$ and $\overline{BC}$ have equal measures. $\overline{MN}$ and $\overline{NO}$ share the same lengths, so we have the following:
\begin{aligned}\overline{MO} &= \overline{BC}\\\overline{MN}+\overline{NO}&= \overline{BC}\\2\overline{MN}&= \overline{BC}\\\overline{MN}&= \dfrac{1}{2}\cdot \overline{BC}\end{aligned}
This confirms the second part of the midpoint. Now that both parts have been proven, we can conclude that the midpoint theorem applies to all triangles. This time, let’s extend our understanding by applying the midpoint theorem to solve different problems in Geometry.
How To Prove a Midpoint in Geometry?
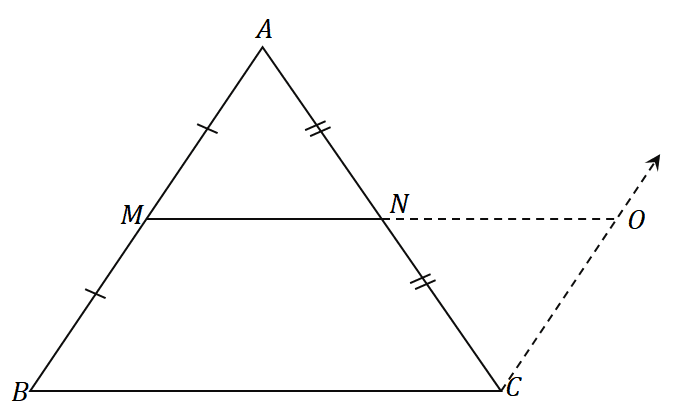
To prove a midpoint in geometry, apply the converse of the midpoint theorem, which states that when the line segment passes through the midpoint of one line and is parallel to the second side, the other end of the line segment will pass through the midpoint of the third side.

Going back to $\Delta ABC$, if $O$ represents the midpoint of $BC$, and if $\overline{MO}$ is parallel to $\overline{AC}$, then the midsegment, $\overline{MO}$, bisects the lines $\overline{AB}$ and $\overline{BC}$. This also applies to the two other midsegments, $\overline{MN}$ and $\overline{NO}$.
| Midsegment | Conserve of Midpoint Theorem |
| \begin{aligned}\overline{MO}\end{aligned} | \begin{aligned} \overline{MO}&\parallel \overline{AC}\\\overline{AM} &= \overline{MB}\\\overline{BO}&= \overline{OC}\end{aligned} |
| \begin{aligned}\overline{MN}\end{aligned} | \begin{aligned} \overline{MN}&\parallel \overline{BC}\\\overline{AN} &= \overline{NC}\\\overline{AM}&= \overline{MB}\end{aligned} |
| \begin{aligned}\overline{NO}\end{aligned} | \begin{aligned} \overline{NO}&\parallel \overline{AB}\\\overline{BO} &= \overline{OC}\\\overline{AN}&= \overline{NC}\end{aligned} |
Use the same principle to prove whether a given point is a line segment’s midpoint. This is most helpful when working with a triangle where we can identify one midpoint and one pair of parallel sides.
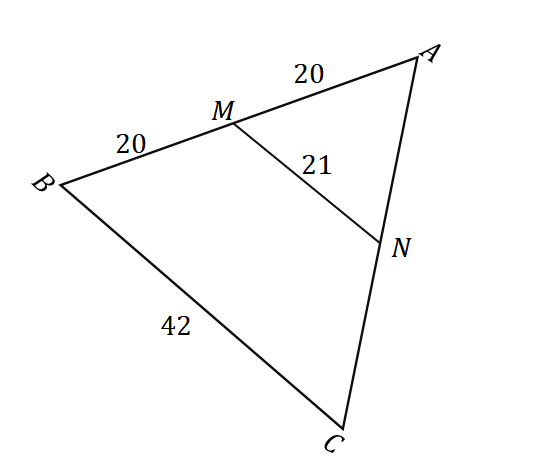
Take a look at the triangle shown above. To prove that $N$ is the midpoint of the line segment $\overline{AC}$, let’s apply the converse of the midpoint theorem. Since $\overline{AM} = \overline{MB}$, $M$ is the midpoint of $\overline{AB}$.
Here are some more relationships that can be observed from $\Delta ABC$:
- The line segment $\overline{MN}$ passes through the point $M$ and is parallel to the second side of the triangle, $\overline{BC}$.
- We can see that $\overline{MN} = \dfrac{1}{2} \cdot\overline{BC}$.
From this, we can conclude that $\overline{MN}$ is a midsegment and it also bisects the third side of the triangle, $\overline{AC}$.
\begin{aligned}\overline{AN} &= \overline{NC}\\&\Rightarrow N \text{ is a midpoint}\end{aligned}
This shows that $N$ is indeed the midpoint of $\overline{AC}$. Apply a similar approach when working with similar problems.
When we know the midpoint theorem and its converse by heart, it opens a wide range of applications and theorems for us to work with. This is why we’ve prepared more examples for you to work on, so head on over to the section below when you’re ready!
Example 1
Using the midpoint theorem and the triangle shown below, what is the value of $x$?
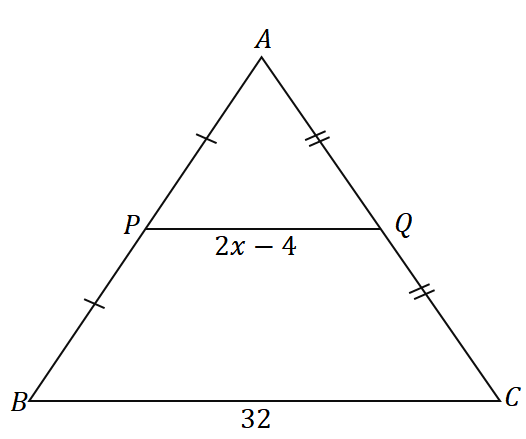
Solution
First, let’s identify whether $P$ and $Q$ are the midpoints of the sides $AB$ and $AC$.
\begin{aligned}\boldsymbol{P}\end{aligned} \begin{aligned}\boldsymbol{Q}\end{aligned}
\begin{aligned}\overline{AP} &= \overline{PB}\end{aligned}
This means that $P$ is indeed a midpoint. \begin{aligned}\overline{AQ} &= \overline{QC}\end{aligned}
Hence, $Q$ is also a midpoint. Now we’ve established that $\overline{PQ}$ passes through the midpoints of the triangle’s sides, $\overline{AB}$ and $\overline{AC}$.
We now have all two conditions to conclude that $\overline{PQ}$ is a midsegment of the triangle. Since $\overline{PQ}$ and $\overline{BC}$ are parallel with each other, we can conclude that the length of $\overline{PQ}$ is half of $\overline{BC}$ through the midpoint theorem.
\begin{aligned}\overline{PQ} &= \dfrac{1}{2} \cdot \overline{BC}\end{aligned}
Use this relationship to establish the equation relating $(2x -4)$ and $32$ then solve for $x$.
\begin{aligned}(2x – 4) &= \dfrac{1}{2}(32)\\2x – 4&= 16\\2x&= 20\\x&= 10\end{aligned}
Hence, we have $x = 10$.
Example 2
Using the converse of the midpoint theorem and the triangle shown below, what is the perimeter of the triangle $\Delta ABC$?
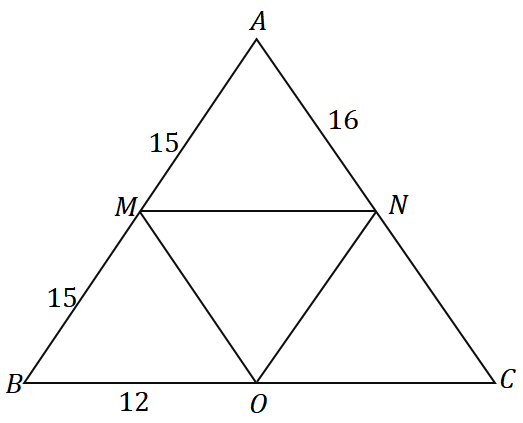
Solution
Since $\overline{AM} = \overline{MB} = 15$, $M$ is the midpoint of $\overline{AB}$. We can see that $\overline{MN}$ passes through the midpoint of $\overline{AB}$ and is parallel to the triangle’s side $\overline{BC}$, so we can conclude that it is indeed the midsegment of $\Delta ABC$.
\begin{aligned}\overline{MN} &\parallel \overline{BC}\\&\Rightarrow N \text{ is the midpoint of } \overline{AC} \end{aligned}
$N$ is the midpoint of $\overline{AC}$, so $\overline{AN} = \overline{NC} = 16$. Applying the same thought process, we can also show that $\overline{MO}$ is a midsegment, so $O$ is also a midpoint.
\begin{aligned}\overline{MO} &\parallel \overline{AC}\\&\Rightarrow O \text{ is the midpoint of } \overline{BC} \end{aligned}
Hence, $\overline{BO} = \overline{OC} = 12$. Now, find the perimeter of $\Delta ABC$ by adding the three sides’ lengths.
\begin{aligned}\text{Perimeter}_{\Delta ABC} &= \overline{AB}+\overline{BC}+ \overline{AC}\\&= 2(\overline{AM})+ 2(\overline{BO}) + 2(\overline{AN})\\&= 2(15) + 2(12) + 2(16)\\&= 86\end{aligned}
This means that the perimeter of $\Delta ABC$ is equal to $86$ units.
Practice Questions
1. The triangle $\Delta ABC$ has $\overline{XY}$ as the midsegment that bisects $\overline{AB}$ and $\overline{AC}$. Which of the following statements is not always true?
A. The line segment $\overline{XY}$ is half the length of $\overline{AB}$.
B. The line segment $\overline{XY}$ is half the length of $\overline{BC}$.
C. The measures of $\angle AXY$ and $\angle ABC$ are equal.
D. The measures of $\angle AYX$ and $\angle ACB$ are equal.
2. Given the triangle $\Delta ABC$ as shown below, what is the length of $\overline{BC}$?
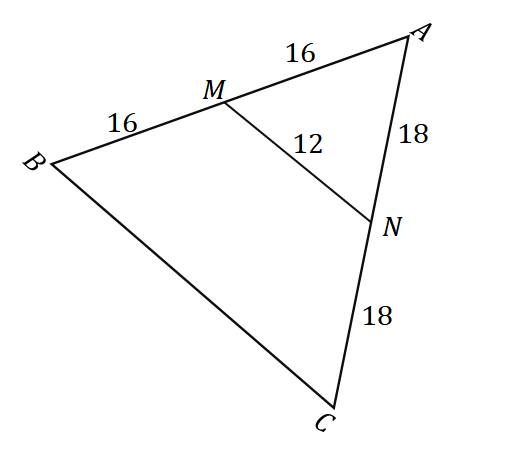
A. $6$ units
B. $8$ units
C. $24$ units
D. $32$ units
3. Given the triangle $\Delta ABC$, what is the perimeter of the triangle shown below?
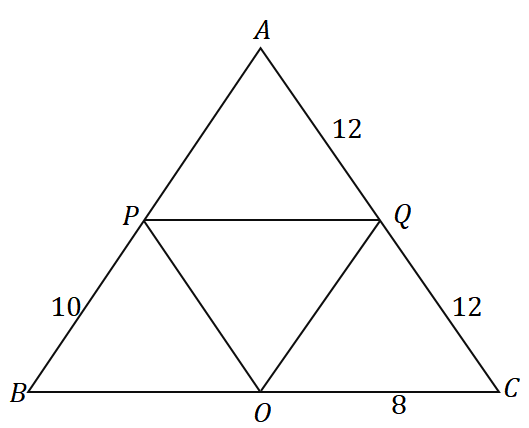
A. $36$ units
B. $48$ units
C. $56$ units
D. $60$ units
Answer Key
1. A
2. C
3. D
