JUMP TO TOPIC

In the realm of mathematical analysis, determining whether a series converges or diverges is a fundamental question. The p-series test provides a valuable tool for investigating the behavior of a specific type of series known as the p-series.
This article delves into the definition of the p-series, explores its properties, and provides a comprehensive understanding of its convergence or divergence.
Definition of P Series Test
The p-series test is a method used to determine the convergence or divergence of a specific type of series called the p-series. A p-series is defined as the sum of the terms (1/nᵖ) for n ranging from 1 to infinity. Mathematically, it can be represented as:
∑(1/nᵖ)
In this representation, the symbol “∑” denotes the summation notation, “n” is the index variable that ranges from 1 to infinity, and “p” is a positive constant.
The p-series test focuses on the value of the exponent “p” to assess the behavior of the series. The test establishes the following criteria:
Convergence (p > 1)
If the value of “p” is greater than 1, the p-series converges. This means that as more terms are added, the sum of the series approaches a finite value. In other words, the series’ partial sums become arbitrarily close to a particular number. Below we present the example of a series convergence in figure-1.
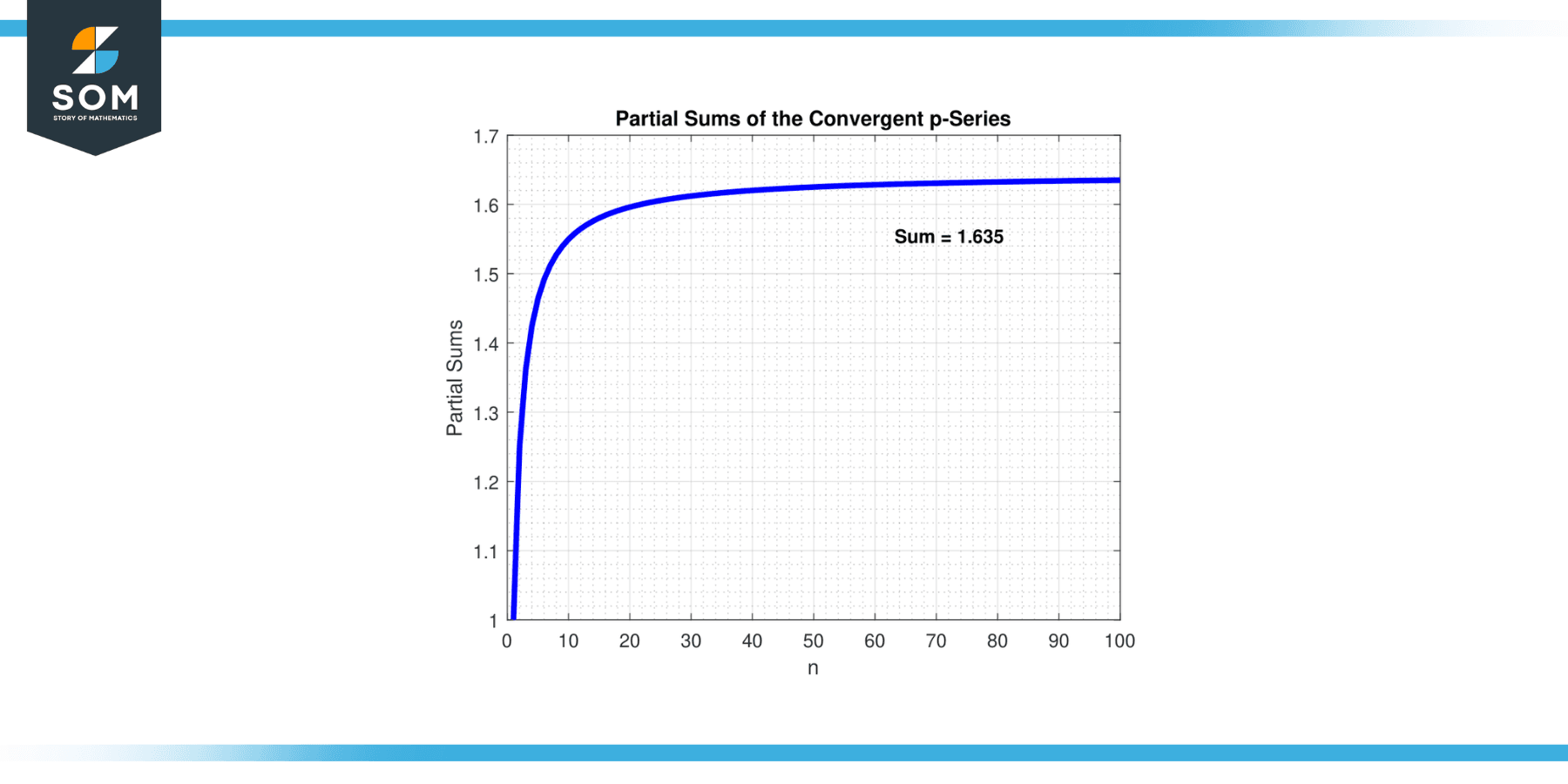
Figure-1.
Divergence (p ≤ 1)
If the value of “p” is less than or equal to 1, the p-series diverges. This means that as more terms are added, the sum of the series becomes infinitely large or approaches infinity. The series of partial sums does not converge to a finite value.
The p-series test provides a clear criterion for determining the convergence or divergence of the p-series based on the value of “p.” It is a straightforward and powerful tool for analyzing the behavior of this specific type of series. Below we present the example of a series divergence in figure-2.
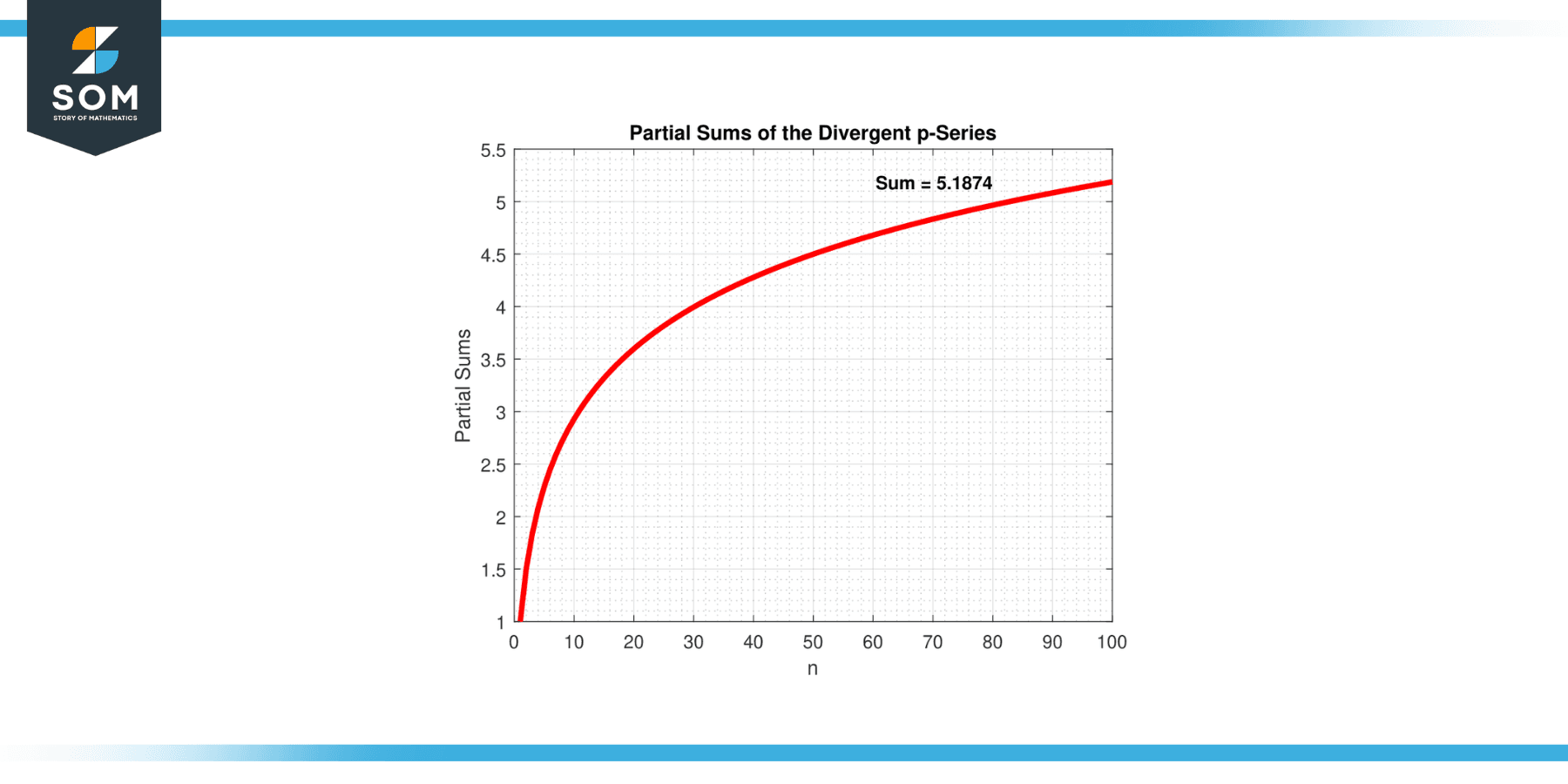
Figure-2.
Historical Significance of P Series Test
The historical significance of the p-series test lies in its contribution to the development of mathematical analysis, particularly in the study of series convergence.
While the test itself may not have a specific historical origin, its principles and applications have been explored by mathematicians over the centuries. Here’s a discussion on the historical significance of the p-series test.
Euler and the Basel Problem
The p-series test gained historical prominence through its association with one of the most famous problems in mathematics—the Basel problem.
In the 18th century, the Swiss mathematician Leonhard Euler used the p-series test to prove that the sum of the reciprocals of the squares (∑(1/n²)) converges to a specific value, $\pi^{2/6}$.
Euler’s solution demonstrated the power of the p-series test as a tool for determining convergence and led to further investigations into the properties of p-series.
Analytic Methods and Convergence Tests
The development and refinement of analytic methods and convergence tests throughout the history of mathematics have contributed to the significance of the p-series test.
Mathematicians such as Augustin-Louis Cauchy, Karl Weierstrass, and Bernhard Riemann expanded upon the concepts underlying the p-series test, developing more general convergence tests and exploring the intricacies of series analysis. The p-series test, as a foundational concept, has served as a stepping stone to these advancements.
Exploration of Series Behavior
The p-series test, along with other convergence tests, has provided mathematicians with a means to understand and classify different series based on their convergence or divergence properties.
This exploration has led to the development of mathematical tools, techniques, and theories that have broad applications in various fields of mathematics, including calculus, analysis, and number theory.
Generalizations and Extensions
The p-series test has also inspired generalizations and extensions, expanding its historical significance. Mathematicians have developed tests such as the Cauchy condensation test, which is a generalization of the p-series test, and the Dirichlet test, which combines aspects of the p-series test with other convergence criteria.
These extensions have enriched our understanding of series convergence and provided additional tools for analyzing various types of series.
Properties
Specific to p-Series
The p-series test is specifically designed to analyze the convergence or divergence of the p-series of the form ∑(1/nᵖ). It is not applicable to other series or more general cases. This specialized nature ensures that the test is most effective when examining p-series.
Borderline Case (p = 1)
When the exponent “p” in the p-series is equal to 1, the series becomes the harmonic series ∑(1/n). In this case, the p-series test is inconclusive.
The harmonic series neither converges nor diverges. It serves as a noteworthy example in the study of series convergence and is often discussed in relation to the p-series test.
Relationship to Other Tests
The p-series test has a connection to other convergence tests, which allows for a more comprehensive understanding of series behavior. Two notable tests often used in conjunction with the p-series test are:
Integral Test
The integral test compares the behavior of a given series with the behavior of an integral. In the context of p-series, the integral test can be employed to prove the convergence of a p-series by comparing it to an appropriate integral. This test provides a powerful tool for establishing convergence.
Comparison Test
The comparison test enables the comparison of a given series with a known convergent or divergent series. By comparing their behavior, conclusions can be drawn about the series in question.
The comparison test can be used in conjunction with the p-series test to strengthen the analysis of series convergence or divergence.
Limitations and Scope
It’s important to note that the p-series test is specific to p-series and cannot be applied universally to all types of series. Other convergence tests are available for different series forms, and the choice of test depends on the specific properties of the series being analyzed.
The p-series test is a valuable tool within its defined scope but should not be applied indiscriminately to all series.
Generalization
While the p-series test focuses on the behavior of the p-series, it has inspired generalizations and extensions in mathematical analysis. For example, the Cauchy condensation test and the Dirichlet test are derived from the p-series test and are applicable to broader classes of series.
These generalizations enhance our understanding of series convergence and provide further tools for analysis.
Applications
The p-series test, with its ability to determine the convergence or divergence of specific types of series, has found applications in various areas of mathematics and beyond. Here are some notable applications of the p-series test.
Series Analysis
The primary application of the p-series test is in the analysis of series convergence. By applying the test to the p-series of the form ∑(1/nᵖ), mathematicians can determine whether a series converges or diverges based on the value of the exponent “p.”
This analysis aids in understanding the behavior of series and helps establish convergence results.
Comparison Tests
The p-series test is often used in conjunction with other convergence tests, particularly comparison tests. By comparing a given series with a known convergent or divergent p-series, mathematicians can deduce the convergence or divergence of the series under consideration. This comparison provides a valuable tool for analyzing a wide range of series.
Calculus and Integration
The p-series test has connections to calculus and integration. It can be used to establish the convergence of improper integrals involving p-series. By comparing an improper integral to an equivalent p-series, mathematicians can determine whether the integral converges or diverges, aiding in the evaluation of integrals and solving problems in calculus.
Harmonic Analysis
The p-series test finds applications in the field of harmonic analysis. The harmonic analysis deals with the decomposition of functions into harmonic components.
The convergence properties of the Fourier series, which are used to represent periodic functions, can be analyzed using the p-series test. This analysis is crucial in understanding the convergence and behavior of Fourier series representations.
Number Theory
The p-series test has implications in number theory, particularly in the study of sums of reciprocals of powers of integers. For example, the p-series test is utilized in investigations related to perfect numbers, which are positive integers that are equal to the sum of their proper divisors.
The convergence properties of series involving the reciprocals of divisors are analyzed using the p-series test to shed light on the properties of perfect numbers.
Physics and Engineering
The p-series test has applications beyond mathematics in disciplines such as physics and engineering. It plays a role in the analysis of infinite series that arise in physical phenomena, including electrical circuits, signal processing, and wave propagation. Understanding the convergence properties of these series is essential in modeling and analyzing real-world systems.
Exercise
Example 1
Determine the convergence or divergence of the series ∑(1/n^3).
Solution
To analyze the convergence or divergence of the series, we can apply the p-series test with “p = 3”. The p-series test states that if the exponent “p” is greater than 1, the series converges; otherwise, it diverges.
In this case, “p = 3” is greater than 1. Therefore, the series ∑(1/n^3) converges. This implies that as more terms are added, the sum of the series approaches a finite value.
Example 2
Investigate the convergence or divergence of the series ∑(1/n⁰˙⁵).
Solution
To determine the convergence or divergence of the series, we can use the p-series test with “p = 1/2”. According to the p-series test, if the exponent “p” is less than or equal to 1, the series diverges.
In this case, “p = 1/2” is not greater than 1. Therefore, the series ∑(1/n⁰˙⁵) diverges. This means that as more terms are added, the sum of the series becomes infinitely large or approaches infinity.
Example 3
Consider the series ∑(1/n⁴) and analyze its convergence or divergence.
Solution
To examine the convergence or divergence of the series, we can apply the p-series test with “p = 4”. According to the p-series test, if the exponent “p” is greater than 1, the series converges.
In this case, “p = 4” is greater than 1. Hence, the series ∑(1/n⁴) converges. As more terms are added, the sum of the series approaches a finite value. Below we present the series convergence in figure-3.
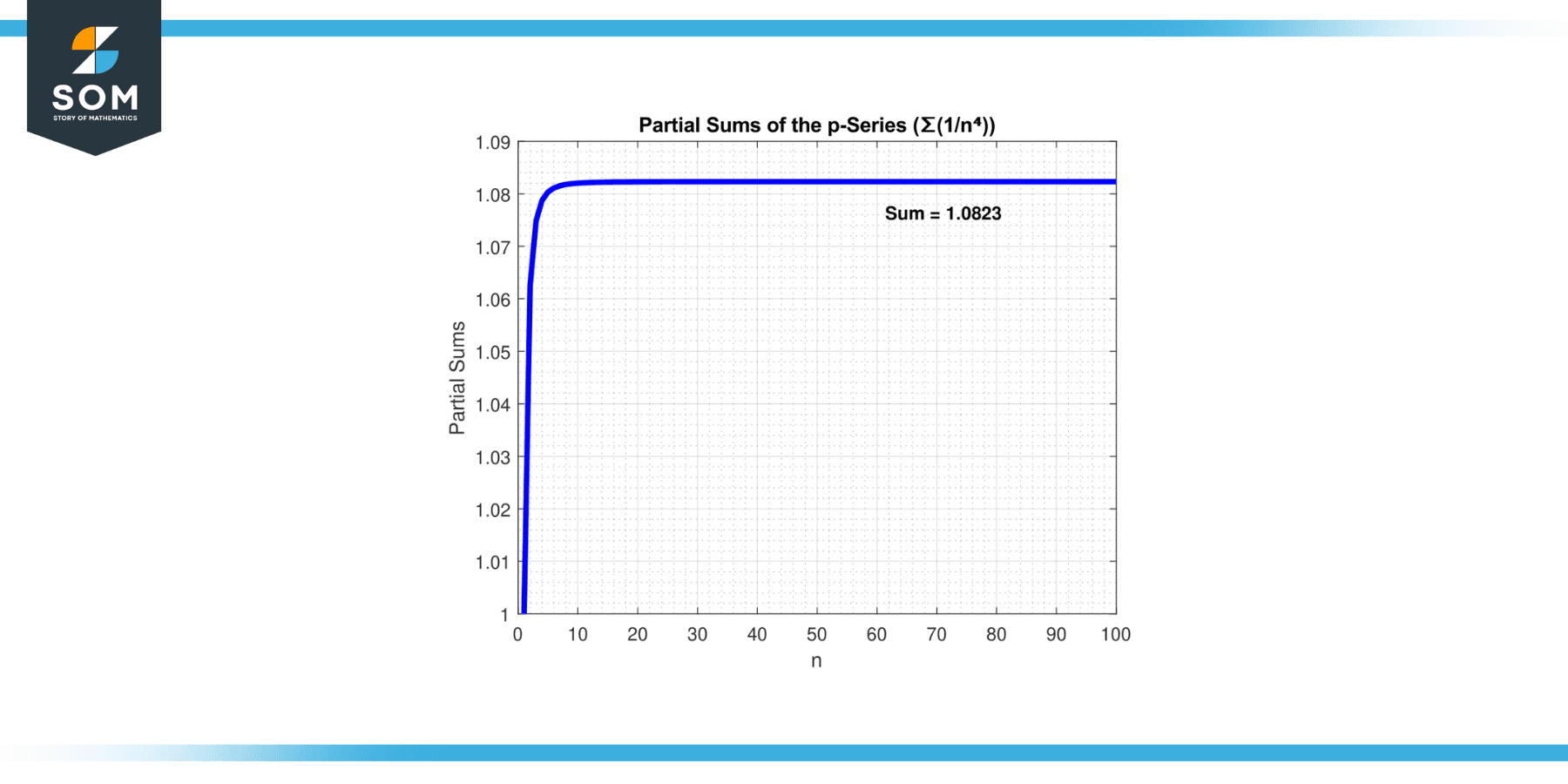
Figure-3
Example 4
Determine the convergence or divergence of the series ∑(1/n).
Solution
To investigate the convergence or divergence of the series, we can utilize the p-series test with “p = 1”. According to the p-series test, if the exponent “p” is equal to 1, the test is inconclusive.
In this case, “p = 1” is not greater than 1. Therefore, the p-series test does not provide a definitive answer regarding the convergence or divergence of the series ∑(1/n). The series in question is known as the harmonic series, and it diverges to infinity.
Example 5
Investigate the convergence or divergence of the series ∑(1/n²).
Solution
To analyze the convergence or divergence of the series, we can apply the p-series test with “p = 2”. According to the p-series test, if the exponent “p” is greater than 1, the series converges.
In this case, “p = 2” is greater than 1. Therefore, the series ∑(1/n²) converges. As more terms are added, the sum of the series approaches a finite value.
Example 6
Determine the convergence or divergence of the series ∑(1/n⁵).
Solution
To determine the convergence or divergence of the series, we can use the p-series test with “p = 5”. According to the p-series test, if the exponent “p” is greater than 1, the series converges.
In this case, “p = 5” is greater than 1. Hence, the series ∑(1/n⁵) converges. As more terms are added, the sum of the series approaches a finite value.
Example 7
Determine the convergence or divergence of the series ∑(1/n⁰˙⁷⁵).
Solution
To investigate the convergence or divergence of the series, we can utilize the p-series test with “p = 3/4”. According to the p-series test, if the exponent “p” is greater than 1, the series converges.
In this case, “p = 3/4” is not greater than 1. Hence, the series ∑(1/n⁰˙⁷⁵) diverges. As more terms are added, the sum of the series becomes infinitely large or approaches infinity.
Below we present the series divergence in figure-4.
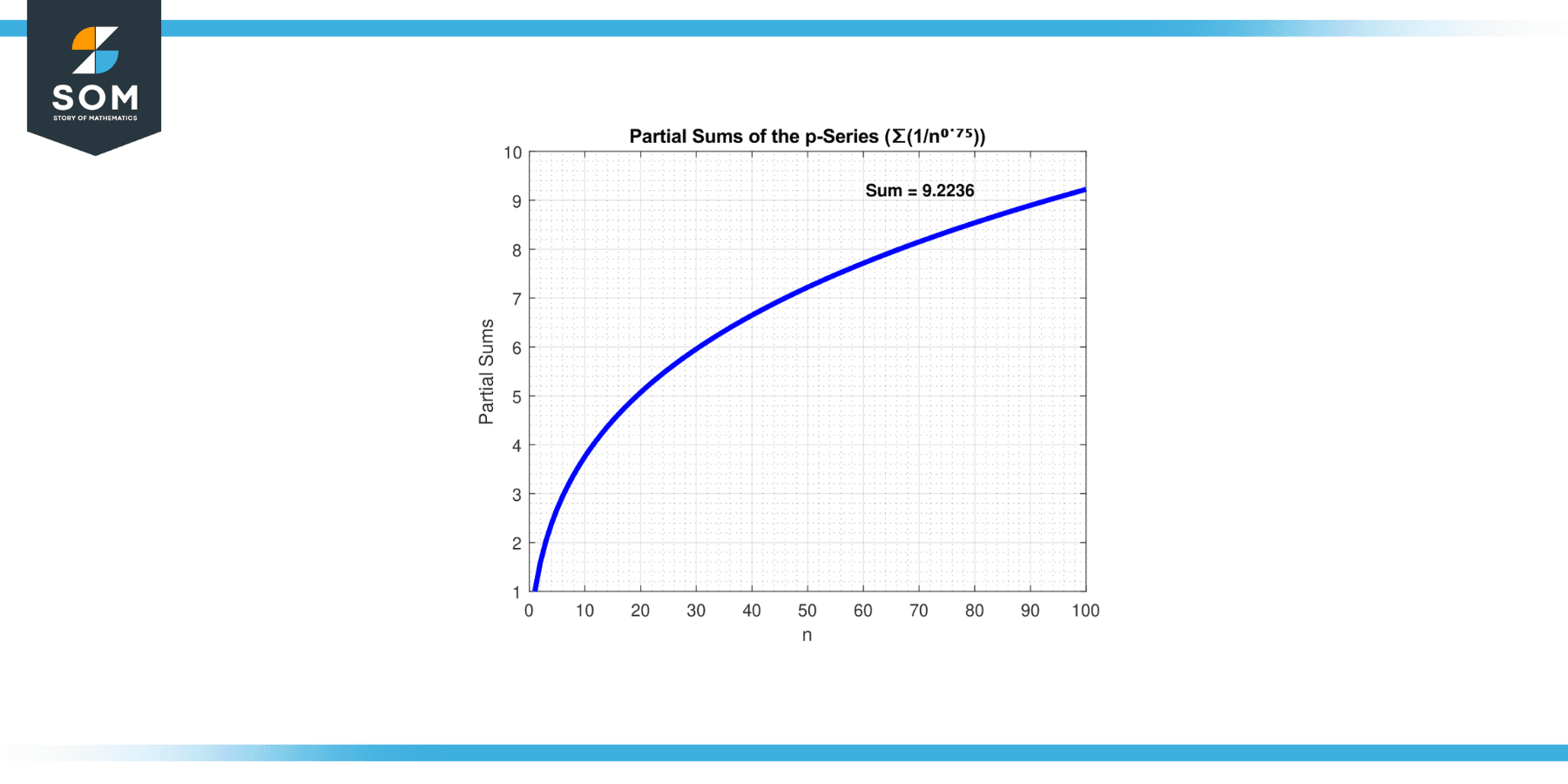
Figure-4
All images were created with MATLAB.
