JUMP TO TOPIC

This discussion aims to illuminate the mathematical properties of secant circles, their relationship with tangents, and the rich tapestry of applications they find in science, engineering, and everyday life.
Definition of Secant Circle
In geometry, a secant circle, with respect to another circle, is a circle that intersects the given circle at exactly two distinct points. These two points are the secant points. If the circles intersect at more than two points or touch each other at one point (becoming tangent circles), they are not considered secant circles.
A “secant circle” isn’t a standard term in geometry. However, “secant” in geometry usually refers to a line intersecting a circle at exactly two points. When applied to two circles, it could mean that the circles intersect at exactly two points.
Hence, “secant circles” can be interpreted as two circles intersecting at exactly two points. In this context, the common chord that connects the two points of intersection can be considered a “secant” to both circles.
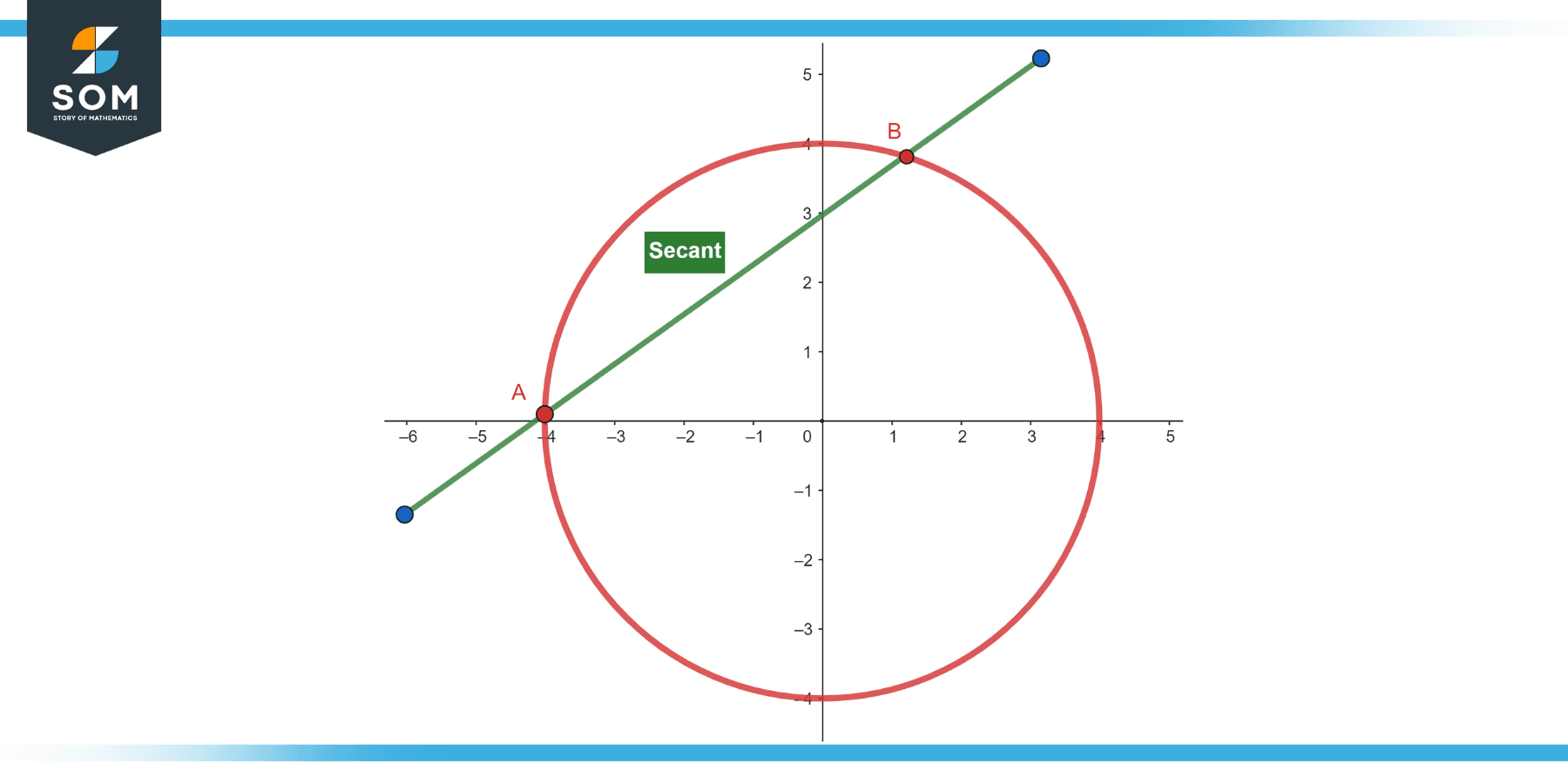
Figure-1.
Properties of Secant Circle
While secant circles do not have distinctive properties, they are part of the wider study of circle geometry involving intersections, secants, and tangents. A secant circle, by definition, intersects another circle at two distinct points. Here are the relevant properties that could apply to secant circles:
Intersection Points
A secant circle intersects the given circle at exactly two distinct points. If there is only one point of intersection, the circles are considered tangent, not secant.
Common Chord
The line segment joining the two points of intersection forms a common chord for the two intersecting circles. This chord divides each circle into two arcs: a major arc and a minor arc.
Angle Between Radii
The angle between the radii drawn from the center of a circle to the two intersection points is called the intercepted angle. The measure of this angle is equal to half the difference of the measures of the intercepted arcs.
Power of a Point
The product of the lengths of two line segments from a point outside a circle to the points of intersection with the circle (when drawn as secant lines) is constant for all such points on a single line passing through the point and the center of the circle.
Cross-Ratio
If two circles are secant at points A and B, any line through A and B intersects the circles again at points C and D (in some order), and the cross-ratio of points A, B, C, D is real and the same for all such lines. This cross-ratio is called the radical ratio of the two circles.
Radical Axis
The locus of points having equal power with respect to two circles forms a line known as the radical axis. The radical axis of two circles is perpendicular to the line joining the centers of the circles and passes through the midpoint of the segment joining the two intersection points.
Orthogonality
Two circles are said to be orthogonal if their radii at the points of intersection are perpendicular. For two secant circles to be orthogonal, the square of the distance between their centers equals the sum of the squares of their radii.
Coaxial System of Circles
If a system of circles all intersect a given circle orthogonally (i.e., at right angles), they are said to form a coaxial system of circles, sharing a common radical axis.
It’s worth noting that the relationships and properties mentioned are derived from the principles of Euclidean geometry and can be applied in solving various geometric problems involving circles and their intersections.
Ralevent Formulas
Secant circles don’t have a unique set of formulas because they are defined merely as two circles intersecting at exactly two points. However, related geometrical concepts, like intersecting circles and chord lengths, have several important formulas:
Length of the Common Chord
If two circles intersect and you know the radii of both circles (r1 and r2) and the distance between their centers (d), you can calculate the length of the common chord (l) using the formula:
l = 2 * √[r1 * (r1 – d)] if d < r1 < 2d (if the center of the circle with radius r1 lies outside the other circle)
l = 2 * √[r2 * (2d – r2)] if d < r2 < 2d (if the center of the circle with radius r2 lies outside the other circle)
Radical Axis
The radical axis of two circles is a line that passes through the two points of intersection of the circles. If the equations of the circles are given by:
(x – a1)² + (y – b1)² = r1²
and
(x – a2)² + (y – b2)² = r2²
then the equation of the radical axis is given by:
(x – a1)² + (y – b1)² – r1² = (x – a2)² + (y – b2)² – r2²
Radical Center
If you have three circles pairwise secant (each pair of circles intersects at two distinct points), they have a common radical axis that passes through a point known as the radical center. The coordinates of the radical center are found by equating the pairwise radical axes and solving for (x, y).
Power of a Point
If a point is outside a circle and is connected to the circle by two lines forming a chord, the power of the point with respect to the circle is given by the product of the lengths of the two line segments, which is a constant for all chords through that point. If the lengths are denoted by d1 and d2, the power is given by d1*d2.
Exercise
Example 1
Two secant circles have radii of 5 cm and 13 cm, and their centers are 12 cm apart. What is the length of the common chord of the two circles?
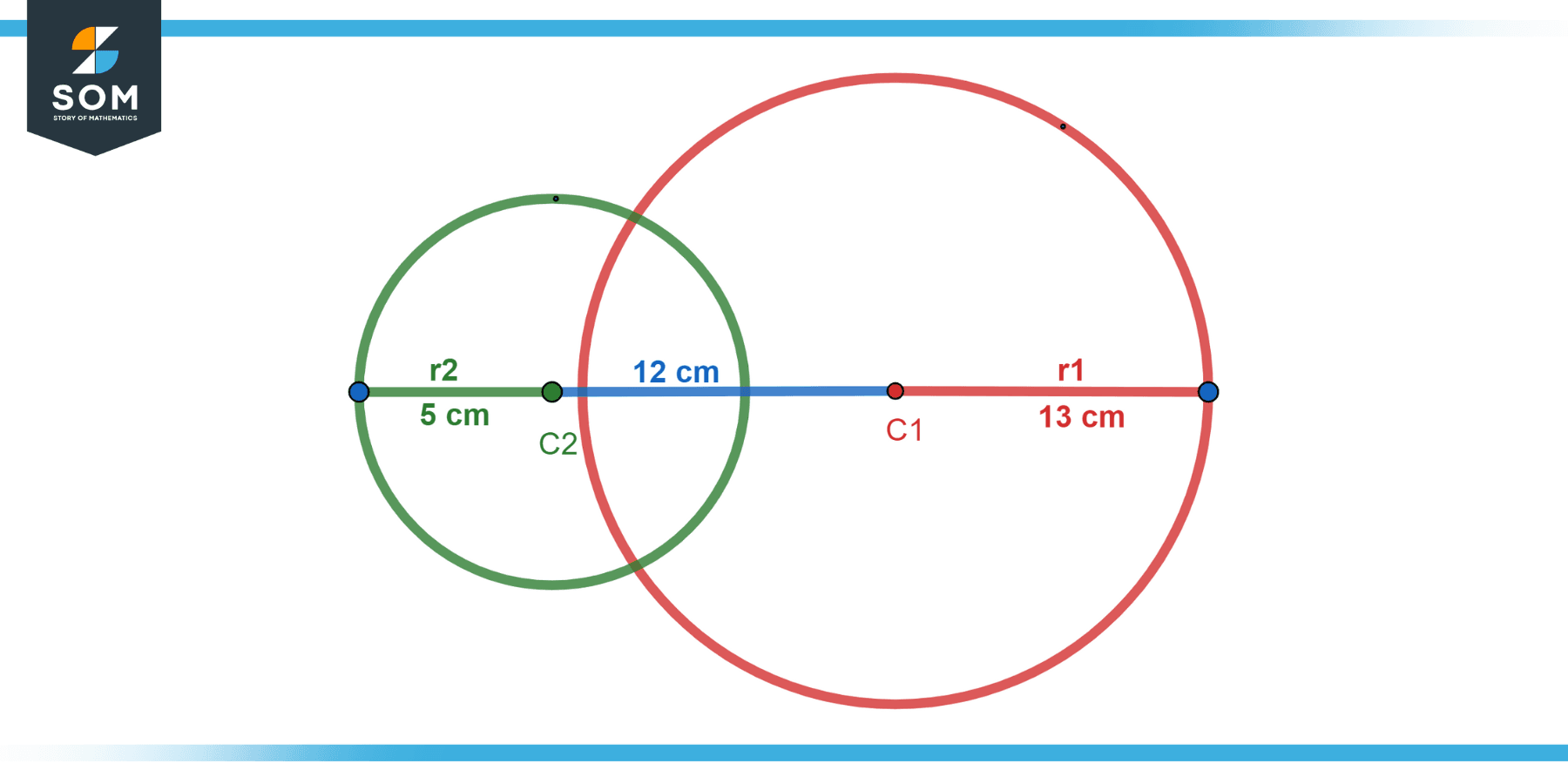
Figure-2.
Solution
The length of the common chord is:
l = 2*(√(13² - 6²) - √(5² - 6²))
l = 2*(√(145) - √(7))
l = 16.528 cm
Example 2
Two circles with radii 7 cm and 9 cm are secant, with their centers 10 cm apart. Determine the length of the common chord.
Solution
The length of the common chord is:
l = 2*(√(9² - 5²) + √(7² - 5²))
l = 2*(√(14) + √(6))
l = 12.198cm
Example 3
Two circles with radii 4 cm and 6 cm are secant, and their centers are 8 cm apart. Find the length of the common chord.
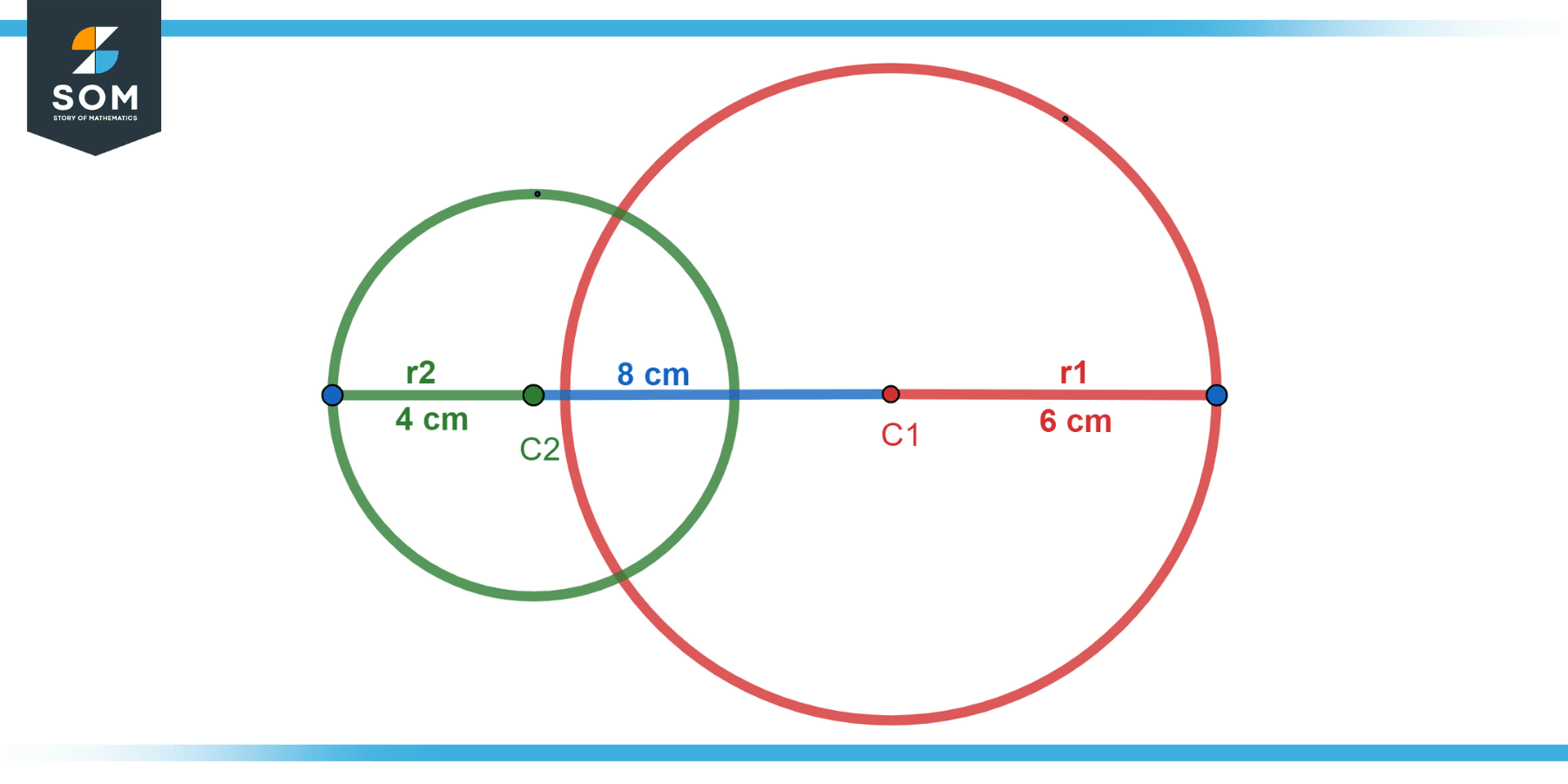
Figure-3.
Solution
The length of the common chord can be calculated using the formula; 2*√(r² - (d/2)²), where r is the circle’s radius and the distance between the centers of the two circles.
Therefore, the length of the common chord is:
ls =2*√(4² - (8/2)²)
ls = = 2*√(16 - 16)
ls = 0 cm
for the smaller circle. And:
ll = 2*√(6² - (8/2)²)
ll = 2*√(36 - 16)
ll = 2*√(20) cm
for the larger circle. Thus, the length of the common chord is 2*√(20) cm.
Example 4
Two secant circles intersect at points A and B. The circles have radii of 15 cm and 9 cm, and the distance between their centers is 14 cm. What is the length of AB?
Solution
The length of AB can be calculated as:
l = √(15² - 7²) + √(9² - 7²)
l = √(134) + √(16)
l = √(134) + 4
l = 14.032 cm
Example 5
Two secant circles have 8 cm and 12 cm radii, and their centers are 16 cm apart. What is the length of the common chord of the two circles?
Solution
The length of the common chord can be calculated as follows:
l = 2*√(12² - (16/2)²)
l = 2*√(144 - 64)
l = 2*√(80) cm
for the larger and smaller circles. Thus, the length of the common chord is 2*√(80) cm.
Applications
While secant circles might not directly find many applications in various fields, the underlying principles of intersecting circles and lines play a vital role in multiple disciplines. Some areas where these concepts come into play include:
Physics
In physics, especially optics, the concept of secant circles is utilized to describe phenomena like lens distortion, spherical aberrations, and the formation of rainbows.
Engineering
Civil engineering principles underlying secant circles help design roundabouts, curved paths, and architectural planning. In mechanical engineering, gears are designed using intersecting circles, which, in a way, behave like secant circles.
Astronomy
The geometry of circles is employed to measure the distances between celestial bodies, to analyze the trajectories of planets and satellites, and to calculate the apparent sizes of stars and planets.
Computer Graphics and Image Processing
Algorithms for drawing circles or arcs and detecting circular objects in images often involve principles associated with secant circles.
Geography and Cartography
Concepts of circle geometry, including tangent and secant properties, are utilized in map projections, where the Earth’s spherical shape is translated onto a two-dimensional surface.
Navigation
In the aviation and maritime sectors, the geometry of the Earth (treated as a sphere or an oblate spheroid) is understood in terms of great circles and small circles, which are related to the concept of secant circles.
Remember that while the concept of secant circles might not be directly applied, the mathematical principles and the underlying geometric intuition form the foundation for many applications in these fields.
All images were created with GeoGebra.
