What Does ‘exp’ Mean in Math? Exploring the Exponential Function

What Does ‘exp’ Mean in Math?

In mathematics, ‘exp‘ refers to the exponential function, which is the function ex, where $e$ is Euler’s number, approximately equal to 2.71828. This function is fundamental in various areas of math, representing continuous growth or decay. 

Introduction

In the world of mathematics, certain functions hold a special place due to their widespread applications and profound mathematical significance. One such function is the exponential function, often denoted as ‘exp.’ The exponential function arises in various branches of mathematics, science, engineering, and finance, playing a pivotal role in modeling growth, decay, and dynamic processes.

This comprehensive guide delves into the meaning of ‘exp‘ in mathematics, explores the properties of the exponential function, and provides practical insights into its real-world applications.

Understanding the Exponential Function

The exponential function, represented by ‘exp(x)’ or ‘e^x,’ where ‘e’ is the base of natural logarithms (approximately 2.71828), is a mathematical construct that describes exponential growth or decay. It has the unique property of producing values that increase (or decrease) rapidly with changes in the input variable ‘x.’ The exponential function is defined as follows:

exp(x) = ex

In this expression, ‘x’ can be any real number, and ‘e’ is Euler’s number, a fundamental constant in mathematics.

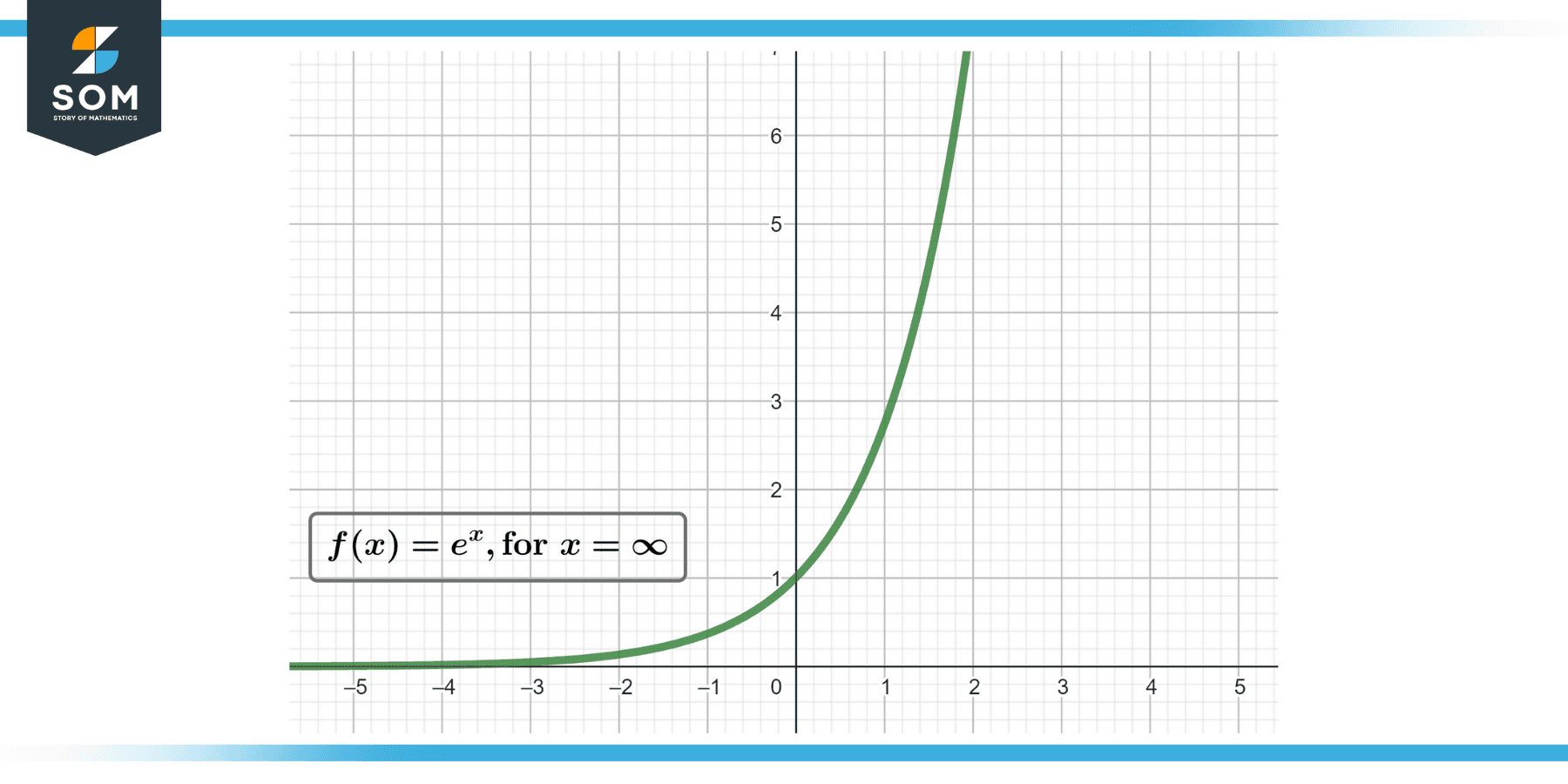
Figure-1: Representation of Exponential Function

Properties of the Exponential Function

The exponential function possesses several key properties that make it a fundamental tool in mathematical modeling and analysis:

Exponential Growth

When ‘x’ is a positive number, ‘exp(x)’ represents exponential growth. As ‘x’ increases, the value of ‘exp(x)‘ grows rapidly, showing a consistent rate of increase. This property is essential in fields such as population growth, compound interest, and microbiology.

Exponential Decay

Conversely, when ‘x’ is a negative number, ‘exp(x)’ represents exponential decay. As ‘x’ decreases, the value of ‘exp(x)’ decreases rapidly, approaching zero but never reaching it. This property is applicable in fields like radioactive decay and cooling processes.

Derivative Property

The derivative of the exponential function is itself, making it unique among functions. In mathematical analysis, this property simplifies the differentiation of complex equations involving exponential functions.

Inverse Function

The natural logarithm function, denoted as ‘ln(x),’ is the inverse of the exponential function. This relationship is fundamental in solving exponential equations and finding rates of change.

Numerical Examples with Solutions

Let’s explore some numerical examples to understand the exponential function better:

Example 1

Exponential Growth

Suppose you invest $1,000 in a savings account that offers an annual interest rate of 5%, compounded annually. Calculate the balance after 5 years using the exponential function.

Solution

The formula for compound interest is:

$A = P(1 + r/n​)^{nt}$

Here, $P=1000$, $r=0.05$, $n=1$ (compounded annually), and $t=5$.

Plugging these values into the formula:

$A = 1000(1 + r/n​)^{1 .5}$

Calculate ‘A’ to find the balance after 5 years.

Example 2

Exponential Decay (Radioactive Decay)

Suppose you have a sample of a radioactive element with a half-life of 10 years. If the initial mass of the sample is 200 grams, calculate the mass remaining after 30 years.

Solution

The formula for exponential decay is:

$N(t) = N0 ​* e^{−λt}$

Here, N0​ = 200 grams, λ = ln(2)/10​, and $t=30$ years.

Plugging these values into the formula:

$N(30) = 200 ​* e^{-30 * ln(2)/10}$

Calculate $N(30)$ to find the mass remaining after 30 years.

Example 3

Continuous Compound Interest (Exponential Growth)

Suppose you invest $5,000 in a savings account with an annual interest rate of 7%, compounded continuously. Calculate the balance after 8 years.

Solution

The formula for continuous compound interest is:

$A = P ⋅ e^{rt}$

Here, $P=5000$, $r=0.07$, and $t=8$ years.

Plugging these values into the formula:

$A = 5000 * e^{0.07 * 8}$

Calculate ‘A’ to find the balance after 8 years.

Example 4

Radioactive Decay Modeling (Exponential Decay)

A sample of a radioactive element initially contains 80 milligrams. If the half-life of the element is 10 days, calculate the amount remaining after 20 days.

Solution

Using the exponential decay formula:

$N(t) = N0 ​* e^ {−λt}$

Here, N0​ = 80 milligrams, λ = 10 * ln(2)​, and $t=20$ days.

Plugging these values into the formula:

$N(20) = 80 ​* e^{-20 * ln(2)/10}$

Calculate $N(20)$ to find the amount remaining after 20 days.

Example 5

Bacterial Growth (Exponential Growth)

In a laboratory experiment, a colony of bacteria doubles in size every 2 hours. If the initial population is 100 bacteria, calculate the population after 6 hours.

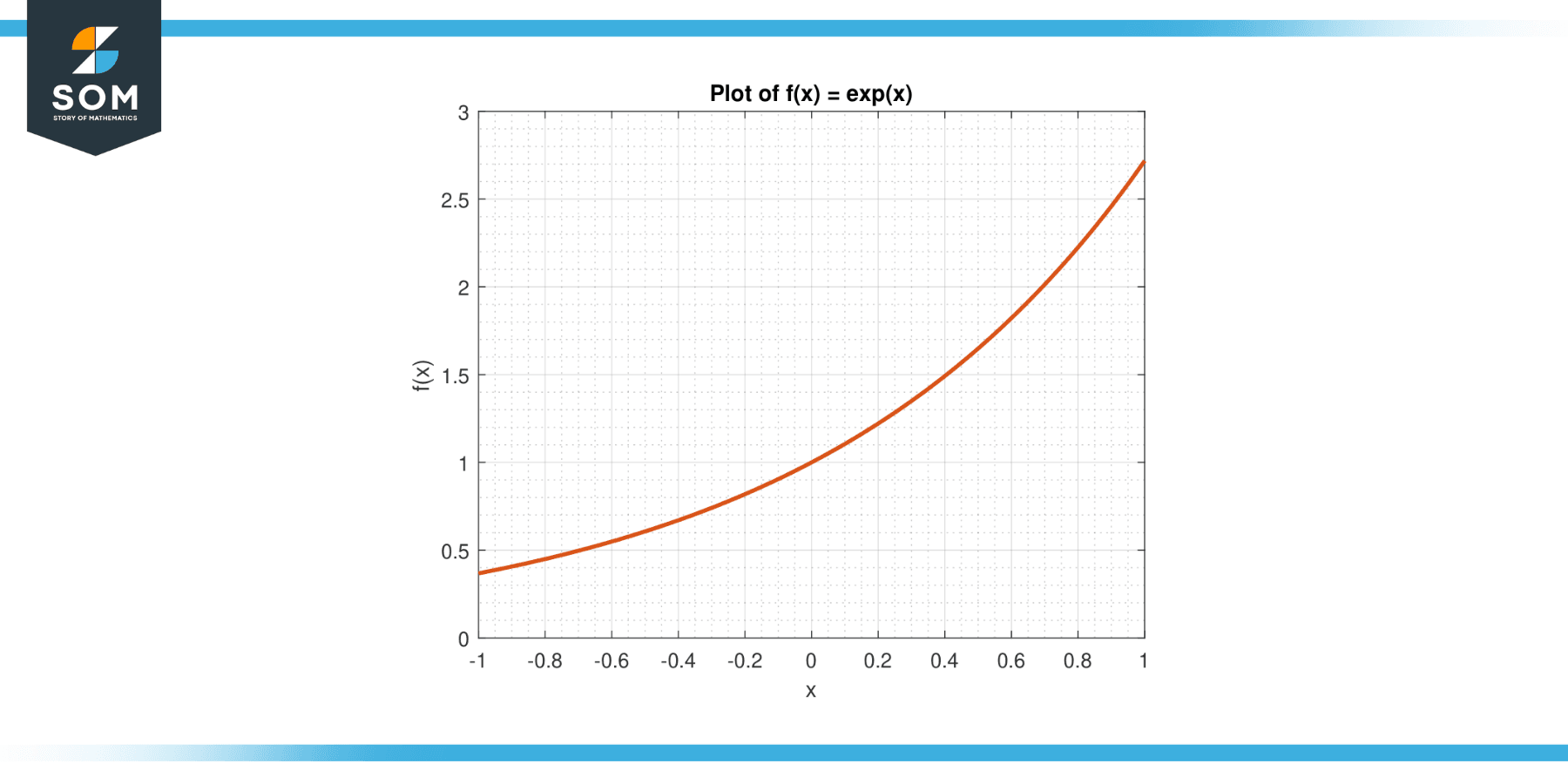
Figure-2: Example of Growing Exponential.

Solution

The exponential growth formula is:

$N(t)=N0​ * 2^{t/k}$

Here, N0​ = 100 bacteria, $k=2$ hours (time for doubling), and $t=6$ hours.

Plugging these values into the formula:

$N(6) = 100 * 2^{6/2}$

Calculate $N(6)$ to find the population after 6 hours.

Example 6

Cooling Process (Exponential Decay)

A cup of hot coffee is left to cool in a room with a constant temperature of 70°F. If the initial coffee temperature is 180°F and it cools down at a rate of 2°F per minute, calculate the coffee temperature after 15 minutes.

Solution

Using the exponential decay formula:

$T(t) = T0​ + (Tr​ − T0​) * e^{−kt}$

Here, T0 ​= 180°F, Tr ​= 70°F, k = cooling rate/ln(2)​ = ln(2)/2 ​, and $t=15$ minutes.

Plugging these values into the formula:

$T(15) = 180 + (70 − 180) * e^{− 15 * ln(2)/2​}$

Calculate $T(15)$ to find the coffee temperature after 15 minutes.

Real-World Applications

The exponential function finds extensive applications in various fields:

Finance

Compound interest calculations, investment growth, and the time value of money are governed by exponential functions, helping individuals and institutions make financial decisions.

Physics

Exponential decay models are used in radioactive decay, nuclear physics, and particle physics to understand the behavior of atomic and subatomic particles.

Biology

Exponential growth models describe population growth, bacterial replication, and the spread of diseases in epidemiology.

Engineering

In engineering, exponential functions are used in fields such as electrical circuits, heat transfer, and fluid dynamics.

Computer Science

Exponential functions play a role in algorithms, computational complexity, and data analysis, especially in tasks involving exponential growth or decay.

Conclusion

The exponential function, denoted as ‘exp‘ in mathematics, is a powerful and versatile tool for modeling growth, decay, and dynamic processes. Its unique properties, including rapid growth, and decay, and the ability to describe rates of change, make it indispensable in various scientific and practical fields.

Whether it’s predicting the future value of an investment, understanding the behavior of radioactive substances, or modeling population growth, the exponential function serves as a mathematical bridge between theory and real-world applications.

By exploring the ‘exp‘ function and its numerical examples, we gain a deeper appreciation for its significance and utility in understanding the dynamic nature of our world.